Что такое тождество в математике

Тождество в математике — это утверждение, которое верно для всех значений переменных, не зависимо от их конкретных значений. Тождество является одним из основных понятий в математике и играет важную роль в доказательствах и решении уравнений.

Тождество — это математическое равенство, которое выполняется для любых значений переменных. Оно является основополагающим понятием в математике и играет важную роль в доказательствах и решении уравнений.

Формально, тождество записывается в виде математического выражения, в котором используются переменные и знаки операций. Например, t + 5 = 2t — 3 — это тождество, так как оно верно для любого значения переменной t.

Одним из основных свойств тождества является то, что оно может быть доказано или опровергнуто. Для доказательства тождества необходимо показать, что оно выполняется для всех значений переменных. В противном случае, если тождество не выполняется хотя бы для одного значения, оно может быть опровергнуто.

Примером тождества может служить выражение a^2 — b^2 = (a — b)(a + b), где a и b — любые числа. Это тождество можно легко проверить, разложив выражение (a — b)(a + b) по формуле разности квадратов.

Тождества имеют широкое применение в различных областях математики, включая алгебру, геометрию и математический анализ. Они позволяют устанавливать связи между различными математическими объектами и выражать их в виде равенств.

Определение тождества в математике

Тождество является основным понятием математической логики и используется для доказательства других математических утверждений. Оно позволяет устанавливать равенства между различными выражениями и операциями, что позволяет упростить вычисления и решения задач.

Примерами тождеств в математике являются:

• Тождество равенства: a = a. Это тождество выполняется для любого значения переменной a.
• Тождество суммы: a + b = b + a. Это тождество говорит о коммутативности сложения и выполняется для любых значений переменных a и b.
• Тождество произведения: a * b = b * a. Это тождество говорит о коммутативности умножения и выполняется для любых значений переменных a и b.
• Тождество дистрибутивности: a * (b + c) = a * b + a * c. Это тождество говорит о дистрибутивности умножения относительно сложения и выполняется для любых значений переменных a, b и c.

Таким образом, тождество в математике — это особое равенство, которое выполняется для всех возможных значений переменных и используется для упрощения и доказательства других математических утверждений.

Видео по теме:

Основные свойства тождеств

1. Симметричность: Если у нас есть тождество A = B, то мы можем сказать, что B = A. Это свойство позволяет нам менять местами значения переменных в рамках тождества.
2. Транзитивность: Если у нас есть тождества A = B и B = C, то мы можем сделать вывод, что A = C. Это свойство позволяет нам строить цепочки равенств и делать выводы на основе уже известных равенств.
3. Ассоциативность: Если у нас есть тождества вида A + (B + C) = (A + B) + C или A \cdot (B \cdot C) = (A \cdot B) \cdot C, то мы можем менять порядок операций в рамках тождества. Это свойство позволяет нам группировать операции по-разному, не меняя их результат.
4. Идентичность: Существуют некоторые специальные значения, которые не меняют другие значения при выполнении определенных операций. Например, для сложения это ноль, для умножения — единица. Такие значения называются идентичными элементами. Например, для любого числа A, будет верным утверждение A + 0 = A, где 0 — идентичный элемент относительно операции сложения.
5. Обратимость: Некоторые операции имеют обратные операции, которые позволяют отменить их результат. Например, для сложения обратной операцией является вычитание, а для умножения — деление. Если у нас есть тождество A + B = C, то мы можем вычесть B из обеих сторон и получить равенство A = C — B.

Знание основных свойств тождеств позволяет нам проводить различные операции и преобразования, упрощая выражения и находя новые равенства.

Примеры тождеств в алгебре

1. Тождество сложения

Для любых чисел a и b выполняется следующее тождество:

a + b = b + a

То есть, порядок слагаемых не влияет на результат сложения.

2. Тождество умножения

Для любых чисел a и b выполняется следующее тождество:

a * b = b * a

То есть, порядок множителей не влияет на результат умножения.

3. Тождество дистрибутивности

Для любых чисел a, b и c выполняется следующее тождество:

a * (b + c) = a * b + a * c

То есть, умножение на сумму чисел равно сумме умножений каждого числа на другое число.

4. Тождество обратного элемента

Для любого числа a существует такое число -a, что выполняется следующее тождество:

a + (-a) = 0

То есть, сумма числа и его обратного элемента равна нулю.

5. Тождество нейтрального элемента

Для любого числа a выполняется следующее тождество:

a + 0 = a

То есть, сумма числа и нейтрального элемента равна числу самому.

Эти примеры тождеств в алгебре помогают установить свойства операций сложения и умножения, а также свойства элементов числовой системы.

Вопрос-ответ:

Что такое тождество в математике?

Тождество в математике — это утверждение, которое верно для любых значений переменных или объектов, которые входят в него. Тождество не зависит от конкретных чисел или объектов, а является истинным по своей сути.

Как можно определить тождество?

Тождество можно определить как утверждение, которое верно для любых значений переменных или объектов, которые входят в него. Оно должно быть истинным независимо от конкретных чисел или объектов, и может быть доказано математическими методами.

Можете привести примеры тождеств в математике?

Конечно! Некоторыми известными примерами тождеств в математике являются: тождество Пифагора (a^2 + b^2 = c^2), тождество двойного угла (sin(2x) = 2sin(x)cos(x)), идентичность Эйлера (e^(iπ) + 1 = 0), и т.д. Все эти тождества верны для любых значений переменных, которые входят в них.

Какова роль тождеств в математике?

Тождества играют важную роль в математике, так как они позволяют устанавливать связи между различными математическими объектами и операциями. Они используются для решения уравнений, вывода новых математических результатов, доказательства теорем и т.д. Тождества помогают упростить сложные выражения и найти общие закономерности.

Каким образом тождества проверяются и доказываются?

Тождества проверяются и доказываются с использованием математических методов и логических рассуждений. Обычно начинают с упрощения выражения или преобразования его в другую форму, а затем применяют известные математические правила и свойства, чтобы проверить, что обе стороны тождества равны или эквивалентны друг другу. Если это удается сделать, то тождество считается доказанным.

Тождества в геометрии

Примером тождества в геометрии может служить теорема Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:

a^2 + b^2 = c^2

где a и b — длины катетов, c — длина гипотенузы.

Тождества в геометрии играют важную роль в доказательствах теорем и свойств геометрических фигур. Они позволяют устанавливать связи между различными геометрическими объектами и выводить новые утверждения на основе уже доказанных фактов.

Тождества в тригонометрии

Одним из наиболее известных тождеств в тригонометрии является тождество Пифагора. Оно утверждает, что для любого прямоугольного треугольника, квадрат гипотенузы равен сумме квадратов катетов. Тождество Пифагора записывается следующим образом:

sin²(θ) + cos²(θ) = 1

где θ — любое значение угла.

Другим примером тождества в тригонометрии является тождество двойного угла для синуса. Оно гласит, что синус двойного угла равен произведению синуса угла и косинуса угла. Тождество двойного угла для синуса записывается следующим образом:

sin(2θ) = 2sin(θ)cos(θ)

где θ — любое значение угла.

Эти тождества являются основными и широко используются в тригонометрии для решения задач и упрощения выражений. Они помогают установить связи между различными тригонометрическими функциями и расширяют возможности анализа углов и треугольников.

Закономерности тождеств в логике

Одной из основных закономерностей является закон идемпотентности. Согласно этому закону, операции «или» и «и» над одним и тем же значением дают то же самое значение. Например, выражение «а или а» всегда равно «а», а выражение «а и а» всегда равно «а».

Другой важной закономерностью является закон дистрибутивности. Согласно этому закону, операции «или» и «и» можно распределить по переменным внутри скобок. Например, выражение «а и (b или с)» равно выражению «(а и b) или (а и с)».

Также в логике существуют законы противоречия и исключения третьего. Закон противоречия гласит, что утверждение и его отрицание не могут быть одновременно истинными. Закон исключения третьего утверждает, что любое утверждение либо истинно, либо ложно, без промежуточных значений.

Это только несколько примеров закономерностей тождеств в логике. Знание этих закономерностей позволяет более точно и строго анализировать и описывать логические выражения и рассуждения.

Применение тождеств в математических доказательствах

Одним из основных способов применения тождеств является замена одного выражения другим, эквивалентным ему согласно определенному тождеству. Это позволяет сократить сложность выражения и перейти к более простым выражениям, которые уже известны или легко решаются.

Применение тождеств также может использоваться для доказательства равенств. Если нужно доказать, что два выражения равны, можно преобразовать одно из них с помощью тождеств и получить другое выражение. Таким образом, доказательство сведется к проверке равенства двух простых выражений.

Например, для доказательства равенства (а + b)^2 = a^2 + 2ab + b^2, можно использовать тождество (a + b)^2 = a^2 + 2ab + b^2 и заменить левую часть равенства на правую согласно данному тождеству. Таким образом, мы показываем, что два выражения эквивалентны и равны друг другу.

В заключение, применение тождеств в математических доказательствах является мощным инструментом, позволяющим упростить выражения, доказывать равенства и решать сложные задачи. Правильное использование тождеств требует глубокого понимания их определений и свойств, а также умение применять их в конкретных ситуациях.

Значимость тождеств в различных областях математики

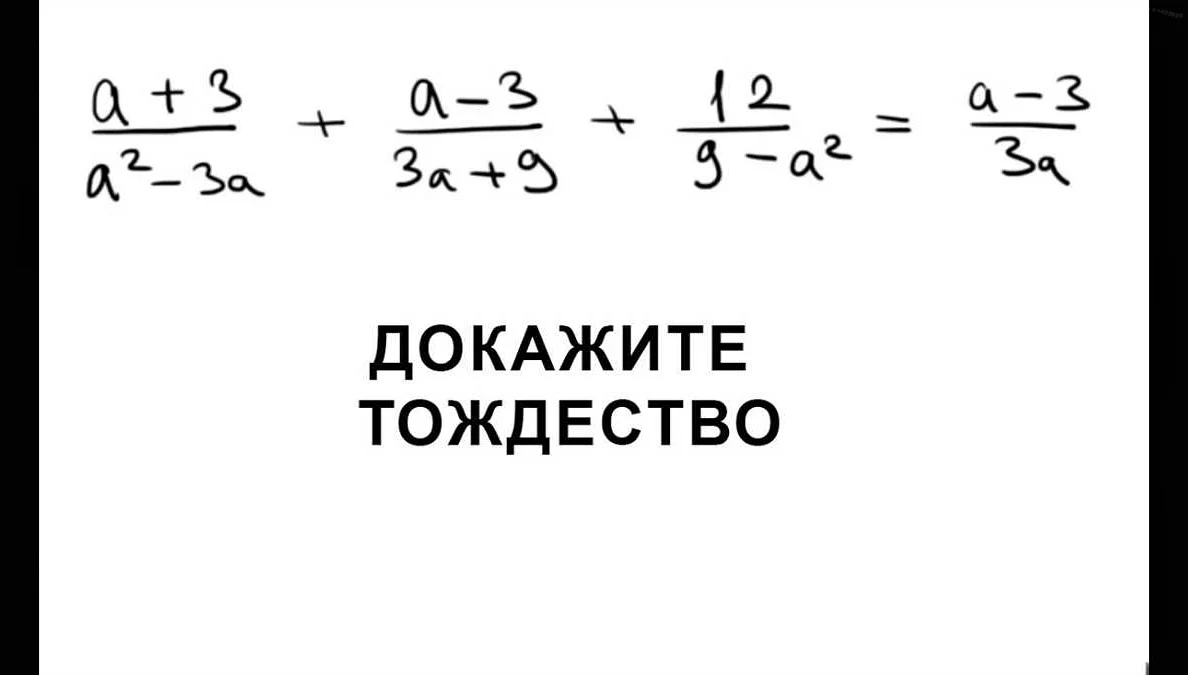
В алгебре и арифметике тождества используются для работы с алгебраическими выражениями, упрощения выражений и решения уравнений. Например, тождество раскрытия скобок позволяет упростить сложные выражения, а тождество коммутативности и ассоциативности позволяют менять порядок операций и объединять слагаемые. Тождества также используются для доказательства свойств алгебраических структур, таких как группы, кольца и поля.

В математическом анализе и теории чисел тождества применяются для доказательства свойств функций, рядов и уравнений. Например, тождество Эйлера позволяет связать понятия экспоненты, мнимой единицы и тригонометрических функций. Тождества также используются для решения задач на нахождение пределов, интегралов и сумм.

В логике и теории множеств тождества используются для формализации и описания логических операций, связей и принципов. Например, тождество двойного отрицания позволяет упростить логическое выражение, а тождество де Моргана связывает операции «и» и «или». Тождества также используются для доказательства теорем и принципов логики и теории множеств.

Тождества имеют важное значение не только в основных областях математики, но и во многих ее приложениях. Например, в физике тождества используются для описания законов и принципов естественных явлений. В информатике и криптографии тождества используются для разработки алгоритмов и защиты информации.