Математическая логика как решать

Узнайте, как решать задачи математической логики с помощью простых и эффективных методов. Научитесь использовать символы, операторы и правила, чтобы логически анализировать и решать математические проблемы. Получите навыки, необходимые для решения сложных математических задач и развития логического мышления.

Математическая логика – это раздел математики, который изучает законы рассуждений и доказательств. Он основан на принципах формальной логики и представляет собой систему символов и правил, которые позволяют строить логические выводы. В математической логике используются такие понятия, как предикаты, переменные, кванторы и логические операторы.

Основные принципы решения задач в математической логике включают в себя анализ условия, выделение ключевых понятий, построение логической схемы решения и проверку полученного результата. При решении задач важно уметь правильно формулировать утверждения и определения, а также применять законы логики для вывода новых фактов из имеющихся.

Например, задача может состоять в том, чтобы доказать или опровергнуть некоторое утверждение, используя имеющиеся факты и логические законы. Для этого необходимо провести цепочку логических рассуждений и доказать или опровергнуть исходное утверждение.

Математическая логика широко применяется в различных областях науки, таких как компьютерная наука, философия, математика и др. Она позволяет строить точные и строгие рассуждения, а также разрабатывать новые теории и модели. Знание основных принципов решения задач в математической логике помогает развивать аналитическое мышление и повышает логическую грамотность.

Понятие математической логики

Основными элементами математической логики являются понятия и символы, которые используются для описания логических операций, отношений и функций. С помощью этих понятий и символов можно формулировать и анализировать математические утверждения, рассуждения и доказательства.

В математической логике используются различные формальные системы, такие как исчисление высказываний, исчисление предикатов, теория множеств и другие. Каждая из этих систем имеет свои правила вывода и аксиомы, которые позволяют проводить логические рассуждения и доказательства.

Математическая логика имеет широкий спектр применений в различных областях науки и техники. Она используется для формализации и анализа различных математических теорий и моделей, а также для разработки и верификации программного обеспечения, искусственного интеллекта и других систем.

Примеры применения математической логики:

Формализация и анализ аксиоматических систем, таких как аксиомы Пеано или аксиомы геометрии.

Разработка и верификация алгоритмов и программного обеспечения.

Исследование логических отношений и свойств в теории множеств.

Анализ формальных языков и грамматик.

Разработка и использование искусственного интеллекта и экспертных систем.

Видео по теме:

Значение математической логики в решении задач

Применение математической логики в решении задач позволяет проявить точность и строгость мышления. Она помогает структурировать информацию и разбить сложную задачу на более простые подзадачи. Такой подход позволяет избежать путаницы и ошибок, а также упрощает процесс решения.

Математическая логика также помогает установить связи между различными фактами и утверждениями. Она позволяет выявить логические закономерности и отношения, которые помогают понять суть задачи и найти правильное решение. Правильное применение математической логики обеспечивает логическую последовательность рассуждений и позволяет получить достоверные и верные ответы.

Кроме того, математическая логика позволяет формализовать задачу и применить формальные методы для ее решения. Она предоставляет инструменты для создания формальных моделей, которые могут быть использованы для анализа и решения задач. Это позволяет упростить задачу и использовать ее абстрактные аспекты для построения решения.

Таким образом, математическая логика имеет большое значение в решении задач. Она помогает структурировать информацию, обнаруживать логические связи и применять формальные методы для получения верных результатов. Правильное применение математической логики позволяет достичь точности и строгости мышления, а также получить достоверные и верные ответы на поставленные вопросы.

Основные принципы

Основными принципами математической логики являются:

1. Принцип идентичности: Если два объекта идентичны, то они равны между собой.
2. Принцип непротиворечивости: Нельзя одновременно утверждать и отрицать одно и то же.
3. Принцип исключенного третьего: Любое утверждение либо истинно, либо ложно.
4. Принцип непротиворечивости: Нельзя одновременно утверждать и отрицать одно и то же.

Эти принципы являются основой для доказательств и рассуждений в математической логике. Они помогают строить логические цепочки и выводы на основе заданных аксиом и правил логики.

Основные принципы математической логики являются универсальными и применимыми в различных областях знаний. Они позволяют анализировать информацию, формулировать гипотезы, доказывать теоремы и решать задачи в различных науках, включая математику, философию, информатику и др.

Принцип идентичности

Принцип идентичности является основой для многих математических рассуждений и доказательств. Он позволяет установить равенство между различными объектами и использовать это равенство в дальнейших рассуждениях.

Принцип идентичности можно использовать для определения равенства между элементами множества. Если два элемента A и B равны, то это означает, что они идентичны и неотличимы друг от друга.

Принцип идентичности также применяется в логических операциях. Например, в логическом умножении (логическом И) идентичность означает, что истинность утверждения «A и B» зависит только от истинности A и B. Если A и B идентичны, то выражение «A и B» будет истинным только в том случае, если A и B истинны. Если A и B неидентичны, то выражение «A и B» будет ложным.

Принцип противоречия

Противоречивые утверждения — это утверждения, которые противоречат друг другу и не могут быть одновременно истинными. Например, утверждение «Солнце светит» и утверждение «Солнце не светит» являются противоречивыми.

Принцип противоречия является одним из основных принципов математической логики, так как он позволяет строить логические выводы и доказательства. Если бы принцип противоречия не существовал, то любое утверждение могло бы быть одновременно истинным и ложным, что привело бы к полному отсутствию логики и невозможности делать выводы.

Принцип противоречия широко используется в математике и других науках для формулировки и доказательства теорем. Он позволяет исключить противоречивые утверждения и установить их истинность или ложность.

ПримерИстинность

Утверждение А: Сегодня понедельник	Истинно
Утверждение В: Сегодня вторник	Ложно

В данном примере утверждение А и утверждение В противоречат друг другу и не могут быть одновременно истинными. Принцип противоречия позволяет определить, что утверждение А является истинным, а утверждение В — ложным.

Принцип исключенного третьего

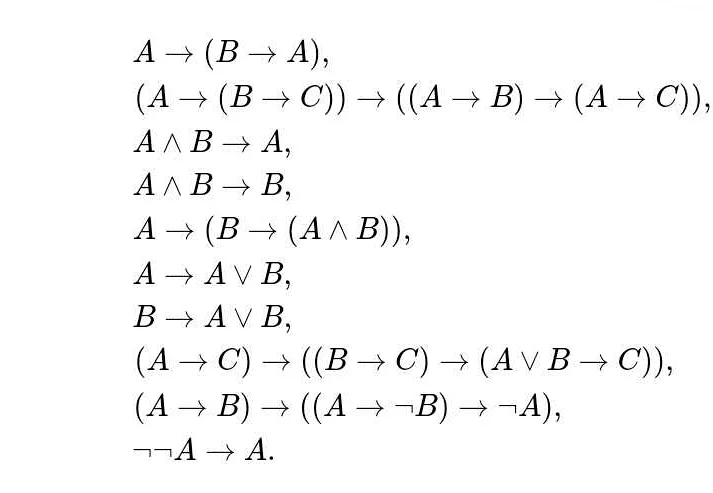
Следуя принципу исключенного третьего, мы можем утверждать, что если у нас есть утверждение A, то оно может быть истинным (A), или ложным (не A). Третьего варианта не существует.

Принцип исключенного третьего широко применяется в математике и логике для формулирования и доказательства теорем. Он позволяет сделать выводы о верности или ложности утверждений на основе логических рассуждений и анализа данных.

Принцип исключенного третьего является основой для многих логических и математических операций, таких как доказательство от противного, построение деревьев вывода и принятие решений на основе анализа возможных вариантов.

Применение принципа исключенного третьего требует точности и аккуратности при формулировке утверждений и доказательств. Неправильное использование этого принципа может привести к некорректным или недостоверным выводам.

Применение в решении задач

1. Доказательство теорем и утверждений. С помощью математической логики можно формализовать и строго доказать различные теоремы и утверждения. Основные принципы математической логики, такие как законы дистрибутивности, закон исключенного третьего и закон противоречия, позволяют строить логические цепочки рассуждений и доказывать различные утверждения.

2. Анализ и построение алгоритмов. Математическая логика играет важную роль в анализе и построении алгоритмов. Логические операции, такие как конъюнкция, дизъюнкция и импликация, позволяют формализовать и описать логические связи и условия в алгоритмах. Это помогает разработчикам понять и оптимизировать работу алгоритмов.

3. Разработка программного обеспечения. Математическая логика также применяется при разработке программного обеспечения. Логические выражения и условия используются для построения алгоритмов и проверки условий. Это помогает разработчикам создавать надежное и эффективное программное обеспечение.

4. Решение задач комбинаторики и теории множеств. Математическая логика имеет важное значение при решении задач комбинаторики и теории множеств. Логические операции, такие как объединение, пересечение и разность множеств, позволяют формализовать и анализировать различные комбинаторные задачи.

Примеры применения математической логики в решении задач:

Доказательство теорем и утверждений

Анализ и построение алгоритмов

Разработка программного обеспечения

Решение задач комбинаторики и теории множеств

Принципы математической логики в алгоритмах

Одним из основных принципов математической логики в алгоритмах является принцип исключённого третьего. Согласно этому принципу, каждое утверждение может быть либо истинным, либо ложным, без третьего варианта. В программировании это выражается в виде логического типа данных, который может принимать только два значения: true (истина) или false (ложь).

Еще одним принципом математической логики, широко используемым в алгоритмах, является принцип контрапозиции. Этот принцип позволяет заменить исходное утверждение на его контрапозицию, то есть инвертировать его и инвертировать его результат. Это может быть полезно при построении алгоритмов, когда необходимо проверить, является ли условие истинным, а затем выполнить действие, если условие ложно.

Также в математической логике применяется принцип доказательства от противного. Он позволяет доказывать утверждение, предполагая, что оно ложно, а затем выводить противоречие. Если предположение о ложности утверждения приводит к противоречию, то оно должно быть истинным. Этот принцип используется в алгоритмах для поиска решений задач, основанных на логических условиях.

Основные принципы математической логики позволяют разработчикам алгоритмов строить логически верные и эффективные решения задач. Они помогают формализовать условия, определить последовательность действий и проверить корректность результатов. Понимание этих принципов является важным для программистов, поскольку они позволяют структурировать и анализировать задачи, а также повышают надежность и производительность программного кода.

Применение математической логики в программировании

Математическая логика играет важную роль в разработке программного обеспечения. Она позволяет программистам применять строгие математические принципы и логические операции для создания эффективных и надежных программ.

Одним из основных применений математической логики в программировании является использование логических операций, таких как логическое И (AND), логическое ИЛИ (OR) и логическое НЕ (NOT). Эти операции позволяют программистам объединять и сравнивать различные условия и принимать решения на основе их значений.

Еще одним применением математической логики в программировании является применение формальной логики для проверки корректности программного кода. Программисты могут использовать математические методы доказательства и рассуждения для проверки, что их программы выполняются корректно и не содержат ошибок.

Также математическая логика позволяет программистам разрабатывать алгоритмы и структуры данных, которые работают эффективно и оптимально. Математические модели и методы позволяют определить наилучшие способы организации данных и выполнения операций.

Важно отметить, что математическая логика не только помогает программистам создавать более эффективные программы, но и способствует развитию аналитического мышления и логического мышления у разработчиков. Она помогает программистам структурировать и анализировать сложные проблемы и находить оптимальные решения.

Применение математической логики в программировании:

Логические операции (AND, OR, NOT)

Проверка корректности программного кода

Разработка эффективных алгоритмов и структур данных

Развитие аналитического и логического мышления программистов

Примеры решения задач с использованием математической логики

Пример 1:

Дано следующее высказывание: «Если сегодня солнечный день, то я пойду на прогулку». Представим это высказывание в виде логической формулы.

ВысказываниеЛогическая формула

Сегодня солнечный день	p
Я пойду на прогулку	q
Если p, то q	p → q

Используя таблицу истинности, можно определить значения p и q и выяснить, будет ли я идти на прогулку в зависимости от погоды.

Пример 2:

Даны следующие высказывания: «Все кошки спят» и «Пушкин — поэт». Представим эти высказывания в виде логических формул.

ВысказываниеЛогическая формула

Все кошки спят	p
Пушкин — поэт	q
Если p и q, то r	p ∧ q → r

Используя таблицу истинности, можно определить, выполняются ли оба высказывания и, следовательно, является ли утверждение «Если все кошки спят и Пушкин — поэт, то что-то происходит» истинным или ложным.

Пример 3:

Дана следующая задача: «На столе лежат три шляпы — белая, черная и красная. Если взять на ощупь одну из шляп и сказать ее цвет, какова вероятность угадать правильно?»

Представим эту задачу в виде логической формулы:

ВысказываниеЛогическая формула

Цвет шляпы — белый	p
Цвет шляпы — черный	q
Цвет шляпы — красный	r
Правильное угадывание	p ∨ q ∨ r

Используя формулу вероятности, можно определить, что шансы угадать правильный цвет шляпы равны 1/3, так как на столе лежат три шляпы.

Приведенные примеры демонстрируют использование математической логики для решения различных задач. Понимание основных принципов математической логики позволяет анализировать и решать сложные задачи, основываясь на логических операциях и высказываниях.

Вопрос-ответ:

Какие основные принципы математической логики?

Основные принципы математической логики включают в себя законы и правила, которые позволяют проводить логические выводы и доказательства. Один из основных принципов — закон исключенного третьего, который утверждает, что любое утверждение либо истинно, либо ложно. Другой основной принцип — закон противоречия, который гласит, что невозможно, чтобы утверждение было одновременно истинным и ложным. Также в математической логике используются правила логического следования, такие как модус поненс (если А, то В, А, следовательно В) и модус толлес (если А, то В, не В, следовательно не А).

Каким образом математическая логика помогает в решении задач?

Математическая логика помогает в решении задач, предоставляя нам инструменты для анализа и выявления логических связей между утверждениями. Она позволяет нам проводить логические рассуждения, делать выводы и доказывать утверждения. В математической логике мы можем использовать законы и правила для построения цепочек рассуждений, основываясь на логических принципах. Это позволяет нам решать сложные задачи и доказывать математические теоремы.

Какие инструменты математической логики можно использовать для решения задач?

Для решения задач в математической логике мы можем использовать различные инструменты. Один из таких инструментов — это использование символов и операций логики, таких как конъюнкция (логическое «и»), дизъюнкция (логическое «или») и отрицание (логическое «не»). Эти операции позволяют нам строить логические выражения, которые отражают логические связи между утверждениями. Мы также можем использовать таблицы истинности и деревья решений для анализа и визуализации логических связей.

Какие основные принципы математической логики существуют?

Основные принципы математической логики включают законы исключённого третьего, противоречия и двойного отрицания. Закон исключённого третьего говорит, что каждое утверждение либо истинно, либо ложно. Закон противоречия утверждает, что нельзя одновременно утверждать и отрицать одно и то же. Закон двойного отрицания утверждает, что двойное отрицание любого утверждения равносильно самому утверждению.

Каким образом математическая логика помогает в решении задач?

Математическая логика помогает в решении задач, так как она предоставляет инструменты для анализа и формализации различных утверждений и выводов. Она позволяет построить логическую цепочку рассуждений, которая помогает логично и последовательно решить задачу. Также она помогает идентифицировать логические ошибки и противоречия в рассуждениях, что позволяет избежать неправильных выводов.

Какие методы и стратегии можно использовать при решении задач, связанных с математической логикой?

При решении задач, связанных с математической логикой, можно использовать различные методы и стратегии. Некоторые из них включают использование таблиц истинности для анализа логических выражений, использование правил вывода и законов логики, анализ и формализацию условия задачи, а также разбиение задачи на более простые подзадачи. Также полезным может быть использование различных логических операций, таких как конъюнкция, дизъюнкция и импликация, для анализа и преобразования утверждений.