Разделом какой науки является математическая логика

Математическая логика является разделом математики, изучающим формальные системы, символическую логику и методы рассуждения. Она занимается изучением законов и принципов верного и неопровержимого рассуждения, а также разработкой формальных моделей для представления и анализа математических и логических высказываний. Понимание математической логики является фундаментальным для понимания других разделов математики и информатики.

Математическая логика является разделом математики, который изучает формальные системы и методы рассуждения. Она основана на символическом представлении и формализации логических высказываний, что позволяет строить точные и строгие доказательства. Математическая логика играет ключевую роль в различных областях науки, включая информатику, философию, физику и искусственный интеллект.

Основные принципы математической логики включают в себя использование формальных языков, аксиоматический метод, правила вывода и символическое представление высказываний. Формальные языки позволяют точно и однозначно описывать логические выражения и высказывания. Аксиоматический метод позволяет строить системы аксиом и правил вывода, которые описывают логические законы и позволяют строить доказательства.

Приложения математической логики включают в себя разработку и анализ алгоритмов, создание логических схем, моделирование систем и решение сложных проблем. Она широко используется в информатике для проектирования и разработки программного обеспечения, а также в искусственном интеллекте для создания интеллектуальных систем и роботов. Математическая логика также играет важную роль в философии, помогая рассуждать логически и анализировать аргументы и утверждения.

Математическая логика является основой для формального представления и рассуждения о знаниях, что делает ее неотъемлемой частью современной науки и технологий.

Развитие математической логики привело к созданию различных систем и формализмов, таких как исчисление высказываний, исчисление предикатов, модальная логика и др. Они позволяют решать самые разнообразные задачи, начиная от простых логических рассуждений и заканчивая сложными вычислительными проблемами. Все это делает математическую логику ценным инструментом для анализа и понимания мира, а также для создания новых знаний и технологий.

Основные понятия математической логики

Одним из основных понятий математической логики является понятие «формального языка». Формальный язык — это строго определенная система символов и правил их комбинирования. Используя формальные языки, математическая логика позволяет описывать и анализировать различные языки и структуры в математике.

Другим важным понятием математической логики является «понятие доказательства». Доказательство — это логический вывод, который позволяет установить истинность некоторого утверждения на основе уже известных истинных утверждений. Математическая логика изучает различные методы и правила доказательства, которые позволяют строить и анализировать доказательства в формальных языках.

Третьим важным понятием математической логики является «понятие логической истинности». Логическая истиность — это свойство утверждений или формул, которое означает, что эти утверждения или формулы верны в любой модели или интерпретации. Математическая логика развивает методы для формального определения и анализа логической истинности утверждений и формул.

Видео по теме:

История развития математической логики

Однако наиболее важный вклад в развитие математической логики был сделан в XIX и XX веках. В XIX веке математики и логики, такие как Жордан, Гермейн и Бул, начали разрабатывать формальную символическую логику и алгебру логики. Это позволило им формализовать математические рассуждения и доказательства, а также создать новые логические операции и правила.

В начале XX века появился новый подход к математической логике, называемый математической логикой первого порядка. Математики, такие как Гецель, Склем и Черч, разработали формальную систему символов и правил для описания математических рассуждений. Это позволило им изучать основы математики и доказывать новые математические теоремы.

Вторая половина XX века была отмечена развитием новых направлений в математической логике, таких как модальная логика, интуиционистская логика и нестандартная логика. Эти направления исследовали новые типы логических операций и систем, которые позволяют формализовать различные аспекты рассуждений и доказательств.

Сегодня математическая логика имеет широкий спектр применений в науке, информатике, философии и других областях. Она является основой для формализации и автоматизации рассуждений, создания компьютерных программ, разработки и анализа алгоритмов, а также исследования фундаментальных вопросов математики и логики.

Аксиоматический метод в математической логике

Аксиомы – это базовые утверждения, которые принимаются без доказательства. Они служат основой для построения логических рассуждений и выводов. Аксиомы не выводятся из других утверждений и не требуют доказательства, они принимаются на веру.

Аксиоматический метод заключается в формализации математической теории с помощью формальной системы. Формальная система состоит из языка, в котором записываются утверждения, и правил вывода, которые определяют, какие утверждения можно получить из уже имеющихся.

Аксиоматический метод имеет несколько преимуществ. Во-первых, он позволяет строго определить основные понятия и свойства в рамках математической теории. Во-вторых, он обеспечивает строгий и четкий способ доказательства утверждений, что позволяет установить их истинность или ложность. В-третьих, аксиоматический метод позволяет строить формальные системы, которые могут быть использованы для решения практических задач и разработки новых математических моделей.

Однако аксиоматический метод имеет и некоторые ограничения. Во-первых, он требует внимательного и формального определения аксиом и правил вывода, чтобы избежать парадоксов и противоречий. Во-вторых, аксиоматический метод не всегда позволяет получить решение реальной проблемы, так как некоторые аксиомы могут быть слишком абстрактными или несоответствующими реальности.

Тем не менее, аксиоматический метод в математической логике является важным инструментом для построения и развития математических теорий. Он позволяет формализовать и систематизировать математические знания, а также доказывать их свойства и применять их в различных областях науки и техники.

Модельная теория в математической логике

Модельная теория основывается на понятии модели, которая является математическим объектом, представляющим интерпретацию формального языка или теории. Модель может быть представлена как множество объектов с заданными отношениями и операциями, которые соответствуют понятиям и символам формального языка или теории.

Одной из основных целей модельной теории является изучение свойств моделей и их отношений с формальными языками и теориями. Модельная теория позволяет определять и проверять истинность или ложность утверждений и формул в рамках заданной модели.

Модельная теория находит применение в различных областях математики и информатики. Она используется, например, в алгебре, геометрии, теории множеств, теории вероятностей и компьютерных науках. Модельная теория позволяет формализовать и изучать различные математические структуры и их свойства с использованием формальных языков и логических методов.

В заключение, модельная теория является важной областью математической логики, которая изучает свойства и структуры формальных языков и теорий с использованием моделей. Она имеет широкие применения в различных областях математики и информатики и позволяет формализовать и изучать различные математические структуры и их свойства с использованием формальных языков и логических методов.

Математическая логика и компьютерные науки

Математическая логика играет ключевую роль в областях компьютерных наук, таких как искусственный интеллект, теория баз данных, формальные методы верификации и программирования.

Использование математической логики позволяет разрабатывать точные и формальные модели вычислений и систем. Она обеспечивает строгие методы для проверки правильности алгоритмов и программ, а также для анализа и решения сложных проблем.

Логический вывод, основанный на математической логике, является важным инструментом в компьютерных науках. Он позволяет делать выводы и рассуждения на основе заданных правил и аксиом. Это основа для разработки и реализации различных алгоритмов и систем.

Математическая логика также используется для формализации и структурирования знаний в компьютерных системах. Она позволяет представлять информацию в виде формальных языков и символов, что упрощает обработку и анализ данных компьютерами.

Кроме того, математическая логика является основой для различных методов искусственного интеллекта, таких как экспертные системы, машинное обучение и автоматическое доказательство теорем. Она позволяет разрабатывать алгоритмы и модели, которые способны анализировать данные, обучаться на основе опыта и делать решения на основе логических выводов.

Таким образом, математическая логика играет важную роль в компьютерных науках, предоставляя формальные методы и инструменты для анализа, решения проблем и разработки различных систем и алгоритмов.

Математическая логика и искусственный интеллект

Одним из основных принципов математической логики, применяемых в искусственном интеллекте, является формализация знаний с помощью логических аксиом и правил вывода. Это позволяет создать модель мира, в которой можно проводить логические рассуждения и делать выводы.

Искусственный интеллект использует математическую логику для решения различных задач, таких как автоматическое доказательство теорем, планирование и принятие решений, обработка естественного языка и машинное обучение. Математическая логика позволяет формализовать проблему, построить модель и применить различные алгоритмы и методы для ее решения.

Искусственный интеллект также взаимодействует с математической логикой через обратную связь. Результаты исследований в области искусственного интеллекта могут влиять на развитие математической логики, а новые методы искусственного интеллекта могут приводить к открытию новых проблем и задач в математической логике.

Таким образом, математическая логика играет важную роль в разработке и применении искусственного интеллекта. Она обеспечивает формализацию знаний и рассуждений, что позволяет создавать более эффективные и интеллектуальные системы.

Приложения математической логики в философии

Одно из главных применений математической логики в философии – это формализация и анализ аргументов. С помощью математической логики можно выразить сложные философские утверждения и аргументы в формальных терминах, что позволяет проводить точный логический анализ и проверять их корректность. Это особенно полезно при изучении философских теорий, так как формализация позволяет выявить потенциальные противоречия и логические ошибки в аргументации.

Ещё одним важным приложением математической логики в философии является анализ понятий и определений. Математическая логика позволяет строить точные формальные определения и изучать их свойства. Это особенно полезно при анализе философских понятий, так как позволяет избежать неоднозначности и нечеткости в их использовании. Формализация понятий также позволяет проводить логически строгие рассуждения и доказательства.

Ещё одним применением математической логики в философии является исследование и построение формальных систем. Формальные системы играют важную роль в философии, так как предоставляют инструмент для формализации и изучения различных философских теорий и концепций. Путем применения математической логики можно строить и анализировать формальные системы, что позволяет проводить точные логические выводы и изучать свойства их аксиом и правил вывода.

ПрименениеОписание

Анализ аргументов	Формализация и анализ философских утверждений и аргументов для проверки их корректности.
Анализ понятий	Построение точных формальных определений и изучение свойств философских понятий.
Исследование формальных систем	Построение и анализ формальных систем для формализации и изучения философских теорий и концепций.

Таким образом, математическая логика играет важную роль в философии, обеспечивая инструменты для анализа, формализации и изучения философских теорий и аргументов. Её применение позволяет проводить точный логический анализ, выявлять потенциальные ошибки и противоречия, а также строить формальные определения и системы для более глубокого понимания философских понятий и концепций.

Применение математической логики в фундаментальных науках

Применение математической логики в фундаментальных науках позволяет сформулировать и проверить различные гипотезы. Она помогает установить логическую связь между различными фактами и явлениями, а также разработать строгие математические модели для их описания.

В физике математическая логика используется для формулировки законов и принципов, которые описывают поведение физических систем. Например, законы Ньютона о движении и законы сохранения энергии и импульса могут быть сформулированы и проверены с помощью математической логики.

В информатике математическая логика играет ключевую роль в разработке алгоритмов и программ. Она позволяет строить логические цепочки и выражения, которые определяют последовательность операций и условия выполнения программы.

В философии математическая логика помогает анализировать и оценивать различные философские теории и концепции. Она позволяет выявить логические ошибки и противоречия в аргументах и рассуждениях.

Таким образом, применение математической логики в фундаментальных науках играет важную роль в развитии и углублении научных знаний. Она позволяет строить строгие и надежные доказательства, а также разрабатывать новые теории и модели.

Вопрос-ответ:

Что такое математическая логика?

Математическая логика — это раздел математики, который изучает формальные языки, методы и принципы рассуждения, используемые в математике и других дисциплинах. Она занимается исследованием математических структур и алгоритмов, а также разработкой формальных систем, которые могут быть использованы для решения различных задач.

Какие принципы лежат в основе математической логики?

Основные принципы математической логики включают в себя законы исчисления высказываний (например, закон исключённого третьего), законы исчисления предикатов (например, закон исключённого среднего) и законы формальных систем (например, закон о двойном отрицании). Эти принципы помогают анализировать и доказывать математические утверждения и решать различные задачи.

Какими способами математическая логика может быть применена в науке и технологиях?

Математическая логика имеет широкий спектр применений в науке и технологиях. Она используется в компьютерных науках для разработки алгоритмов и программного обеспечения, а также для формального анализа и верификации программ. Она также применяется в искусственном интеллекте для создания логических систем и роботов. В философии она используется для анализа и оценки рассуждений и аргументации. Кроме того, математическая логика находит применение в математике самой, помогая формализовать и доказывать математические теоремы.

Какие основные направления исследований в математической логике?

В математической логике исследуются различные направления, включая исчисление высказываний, исчисление предикатов, теорию множеств, теорию моделей, теорию алгоритмов и теорию доказательств. Каждое из этих направлений имеет свои специфические методы и проблемы, и исследователи стремятся разрабатывать новые теории и методы для решения сложных математических и логических задач.

Что такое математическая логика?

Математическая логика — это раздел математики, изучающий формальные системы и методы рассуждений. Она занимается изучением логических законов и правил, которые лежат в основе математических доказательств и рассуждений.

Какие основные принципы лежат в основе математической логики?

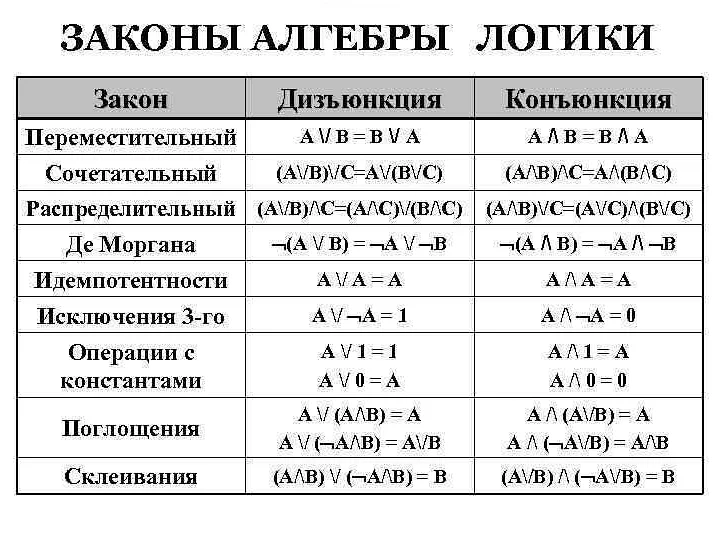
Основные принципы математической логики включают в себя законы и правила логического вывода, такие как закон исключенного третьего, законы де Моргана, законы ассоциативности и дистрибутивности, модус поненс и модус толленс и многие другие.