Математические модели что это

Математические модели — это инструменты, используемые для описания и анализа сложных систем и явлений с помощью математических уравнений и формул. Они позволяют предсказывать поведение объектов и делать выводы на основе математических моделей, что является основой для принятия решений в различных областях науки и техники.

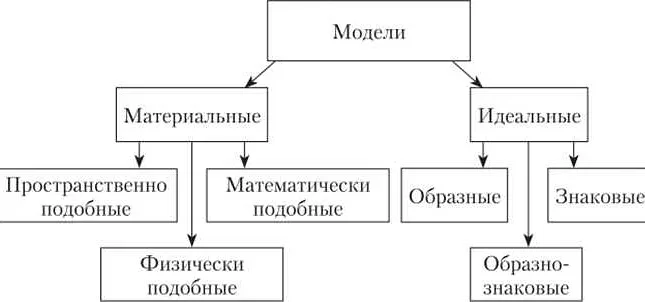
Математические модели – это абстрактные представления реальных систем, созданные для анализа и понимания их работы. Они используются в различных областях науки, техники и бизнеса, чтобы помочь в принятии решений и предсказании результатов.

Одна из основных задач математических моделей – описать сложные процессы с помощью формул и уравнений. Это позволяет ученому или инженеру взглянуть на систему под другим углом и проанализировать ее поведение в различных условиях.

Математические модели широко применяются в физике, биологии, экономике, социологии и других дисциплинах. Например, они позволяют предсказывать движение планет, моделировать эволюцию популяции, определять оптимальные стратегии бизнеса и многое другое.

Использование математических моделей требует не только знания математики, но и глубокого понимания изучаемой системы. Они помогают упростить сложные физические и социальные явления, создавая абстрактные модели, которые можно анализировать и тестировать.

Таким образом, математические модели являются мощным инструментом для исследования и прогнозирования различных систем. Они помогают ученым и специалистам делать более обоснованные решения, экономить время и ресурсы, а также предсказывать результаты исследований или экспериментов.

Что такое математические модели?

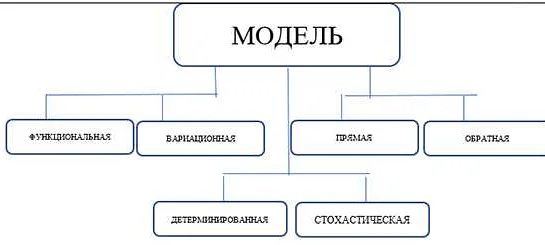
Математические модели помогают нам лучше понять сложные процессы и взаимодействия в различных областях науки, техники и экономики. Они позволяют исследовать различные сценарии и оптимизировать решения, прогнозировать поведение системы, а также проводить эксперименты и анализировать данные.

Применение математических моделей широко распространено в таких областях, как физика, химия, биология, экономика, инженерия, компьютерные науки и социальные науки. Они используются для моделирования физических процессов, прогнозирования погоды, оптимизации производственных процессов, разработки новых лекарств и многого другого.

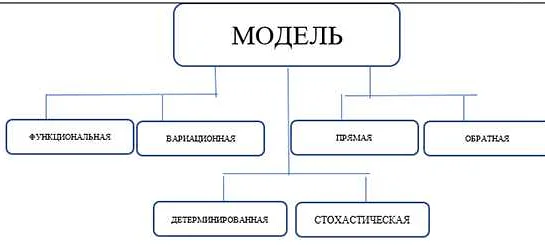
Математические модели могут быть различных типов: детерминистические (основанные на точных уравнениях и известных параметрах), стохастические (учитывающие случайные факторы), дискретные (моделирующие дискретные события) и непрерывные (моделирующие непрерывные процессы).

Использование математических моделей позволяет нам получать качественное и количественное понимание сложных систем, принимать обоснованные решения и предсказывать различные сценарии. Они являются важным инструментом в научных исследованиях и практических приложениях.

Определение и суть математических моделей

Математическая модель представляет собой упрощенное описание реальной системы или явления с помощью математических символов и формул. Она позволяет анализировать и предсказывать поведение системы в различных условиях.

Суть математической модели заключается в том, что она строится на основе определенных предположений и упрощений, которые позволяют сделать систему понятной и изучаемой. Модель может содержать различные элементы, такие как уравнения, графы, таблицы и диаграммы.

Основная цель математической модели — увидеть все возможные взаимосвязи и зависимости между переменными, определить влияние различных факторов на систему и предсказать ее поведение в будущем. Модель может быть использована для оптимизации системы, принятия решений и планирования.

Математические модели используются во многих областях науки и техники, таких как физика, биология, экономика, социология и др. Они помогают упростить сложные системы и явления, а также облегчить их изучение и предсказание. Важно отметить, что математическая модель не является полной копией реальной системы, а лишь ее абстракцией, которая удобна для анализа и исследования.

Выводы, сделанные на основе математической модели, могут быть проверены с помощью экспериментов и наблюдений в реальных условиях. Если модель оказывается достаточно точной и предсказывает поведение системы с высокой достоверностью, она может быть использована для прогнозирования и принятия решений в практических задачах.

Примеры математических моделей

Математические модели используются в различных областях науки и техники для описания и анализа реальных явлений. Ниже приведены несколько примеров математических моделей, которые используются в различных областях:

1. Модель экономического роста: математическая модель, используемая для изучения экономического развития и роста. Она может учитывать такие факторы, как население, инвестиции, производство и потребление, и позволяет прогнозировать экономические показатели в будущем.

2. Модель распространения заболеваний: математическая модель, используемая для изучения и прогнозирования распространения инфекционных заболеваний. Она учитывает такие факторы, как скорость передачи инфекции, иммунитет населения, и позволяет определить эффективность различных стратегий контроля заболевания.

3. Модель движения тела: математическая модель, используемая для описания движения тела в пространстве. Она может учитывать такие факторы, как сила тяжести, сопротивление среды, масса и форма тела, и позволяет предсказать траекторию движения и другие параметры объекта.

4. Модель климатических изменений: математическая модель, используемая для изучения и прогнозирования климатических изменений. Она учитывает такие факторы, как атмосферные условия, океанские течения, распределение тепла и влаги, и позволяет анализировать долгосрочные тенденции и возможные последствия изменения климата.

Это только некоторые примеры математических моделей, которые используются в науке и технике. Они помогают ученым и инженерам лучше понять и предсказать различные явления и процессы, а также разрабатывать эффективные стратегии и решения.

Зачем нужны математические модели?

Одной из основных причин использования математических моделей является возможность получения количественных данных о системе или явлении. Математические модели позволяют определить взаимосвязи между различными переменными и параметрами, а также установить зависимости и закономерности.

Математические модели также помогают сократить время и затраты на проведение экспериментов. Вместо того чтобы проводить дорогостоящие и длительные исследования в реальном мире, исследователи могут создать и анализировать модели в виртуальной среде, что позволяет быстрее и дешевле получить результаты.

Кроме того, математические модели позволяют проводить различные сценарные анализы и оптимизации. Исследователи могут менять значения переменных и параметров в модели, чтобы оценить, как эти изменения повлияют на систему. Такие анализы могут быть полезными при принятии решений и определении оптимальных стратегий.

Наконец, математические модели могут использоваться для предсказания будущих событий и результатов. Анализировая исторические данные и учитывая текущие условия, исследователи могут создать модель, которая позволяет прогнозировать будущие сценарии и предвидеть возможные исходы.

Предсказание и прогнозирование

Математические модели широко используются для предсказания и прогнозирования различных явлений и процессов. Они позволяют предсказать будущие события на основе имеющихся данных и обобщенных закономерностей.

Предсказание и прогнозирование позволяют решать множество задач в различных областях. Например, в экономике модели используются для прогнозирования цен на товары, инфляции, валютных курсов и других экономических показателей. В метеорологии модели позволяют предсказывать погоду на основе данных о температуре, давлении, влажности и других параметрах. В медицине модели используются для прогнозирования распространения заболеваний, эффективности лечения и других медицинских показателей.

Для создания математической модели предсказания и прогнозирования необходимо иметь достаточное количество данных о процессе, который требуется предсказать. Затем данные анализируются, и на их основе строится математическая модель. Модель может быть статистической, детерминированной или иметь другую форму, в зависимости от характера явления.

Прогнозы, полученные с помощью математических моделей, могут быть полезными для принятия важных решений. Например, предсказание роста или спада цен на фондовом рынке может помочь инвесторам принять решение о покупке или продаже акций. Прогноз погоды может помочь людям планировать свои активности на улице.

Однако следует помнить, что математические модели не всегда являются идеальными предсказателями. Они основаны на данных и предположениях, которые могут быть неполными или неточными. Кроме того, будущие события могут быть подвержены случайным факторам, которые модель не учитывает. Поэтому прогнозы, полученные с помощью математических моделей, следует рассматривать как вероятностные оценки.

В целом, предсказание и прогнозирование на основе математических моделей являются важным инструментом для принятия решений в различных областях. Они помогают понять закономерности происходящих процессов и предсказать их развитие в будущем.

Оптимизация и принятие решений

Оптимизация заключается в поиске наилучшего значения для определенной целевой функции при заданных ограничениях. Математические модели могут использоваться для оптимизации различных процессов и систем, таких как производство, логистика, финансы и другие.

Для оптимизации можно использовать различные методы, такие как методы линейного программирования, динамического программирования, генетические алгоритмы и другие. Каждый метод имеет свои особенности и применяется в зависимости от поставленной задачи и доступных данных.

Принятие решений также является важной частью математических моделей. Модели позволяют анализировать различные варианты и предсказывать результаты различных решений. Это помогает принимать обоснованные решения и уменьшать риски.

Математические модели могут использоваться для принятия решений в различных сферах, таких как экономика, бизнес, инженерия и другие. Они позволяют учитывать различные факторы и ограничения, такие как стоимость, время, ресурсы и другие, и выбирать наилучший вариант.

Примеры оптимизации и принятия решений с помощью математических моделей:

Оптимизация производственного процесса для максимизации прибыли и минимизации затрат

Оптимальное распределение ресурсов для достижения максимальной эффективности

Прогнозирование спроса на товары для оптимального управления запасами

Оптимизация маршрутов доставки для сокращения времени и стоимости

Применение математических моделей

Математические модели широко применяются в различных областях науки, техники и бизнеса. Они позволяют описывать и изучать сложные явления и процессы, а также предсказывать и оптимизировать их поведение. Применение математических моделей позволяет получить более точные и надежные результаты, а также сэкономить время и ресурсы.

Одним из наиболее распространенных применений математических моделей является прогнозирование. Математические модели позволяют предсказывать различные события и явления на основе имеющихся данных. Например, в экономике математические модели используются для прогнозирования тенденций рынка, определения оптимальных цен и объемов производства.

Еще одним важным применением математических моделей является оптимизация. Математические модели позволяют найти оптимальные решения в сложных задачах, где требуется учесть множество факторов и ограничений. Например, в логистике математические модели позволяют оптимизировать маршруты доставки грузов, учитывая различные факторы, такие как расстояние, время и стоимость.

Также математические модели применяются в физике, биологии, медицине и других научных областях. Они помогают исследователям лучше понять сложные процессы и явления, такие как движение тел, эволюция популяций или распространение заболеваний. Математические модели позволяют проводить виртуальные эксперименты и тестирования, что сокращает затраты на реальные исследования и повышает безопасность.

В бизнесе математические модели применяются для принятия решений, планирования и анализа данных. Например, в финансовой сфере математические модели используются для расчета рисков, определения оптимальных портфелей инвестиций и прогнозирования доходности. В маркетинге математические модели помогают оптимизировать рекламные кампании, предсказывать спрос и анализировать поведение потребителей.

Область примененияПримеры

Экономика	Прогнозирование рынка, оптимизация производства
Логистика	Оптимизация маршрутов доставки, управление запасами
Физика	Моделирование движения тел, расчет оптических систем
Биология	Моделирование эволюции популяций, исследование молекулярных взаимодействий
Медицина	Прогнозирование распространения заболеваний, оптимизация лечения
Финансы	Расчет рисков, оптимизация портфеля инвестиций
Маркетинг	Оптимизация рекламных кампаний, прогнозирование спроса

Таким образом, математические модели играют важную роль в науке, технике и бизнесе. Они позволяют проводить исследования, прогнозировать и оптимизировать различные процессы и явления. Применение математических моделей позволяет получить более точные и надежные результаты, а также сэкономить время и ресурсы.

В физике и инженерии

Математические модели играют важную роль в физике и инженерии. Они позволяют ученым и инженерам предсказывать поведение физических систем и разрабатывать новые технологии.

В физике математические модели используются для описания физических явлений, таких как движение объектов, электромагнитные поля или взаимодействие частиц. Они позволяют ученым проводить эксперименты на компьютере, а не в реальности, что сокращает затраты времени и ресурсов.

В инженерии математические модели помогают проектировать и оптимизировать различные системы и устройства. Например, они используются для проектирования автомобилей, самолетов, электроники и многого другого. Модели позволяют инженерам предсказывать, как будет вести себя система в разных условиях и проводить виртуальные испытания.

Использование математических моделей в физике и инженерии позволяет ученым и инженерам более глубоко понять и описать сложные физические процессы и принимать обоснованные решения. Они становятся незаменимым инструментом для исследований и разработок в этих областях.

Вопрос-ответ:

Что такое математические модели?

Математическая модель — это абстрактное представление реальной системы, основанное на математических уравнениях и формулах. Она позволяет описать и изучить сложные явления и процессы, которые не всегда можно изучить непосредственно с помощью экспериментов или наблюдений.

Какие преимущества использования математических моделей?

Использование математических моделей позволяет упростить исследование и предсказание сложных систем, таких как погода, экономика, трафик и т. д. Они помогают экономить время и ресурсы, предоставляя возможность проводить эксперименты и тестирование в виртуальной среде. Кроме того, математические модели могут помочь прогнозировать будущие события и принимать обоснованные решения.

Какие виды математических моделей существуют?

Существует несколько видов математических моделей, включая статические модели, динамические модели, вероятностные модели и оптимизационные модели. Статические модели используются для описания состояния системы в определенный момент времени. Динамические модели позволяют предсказывать изменения состояния системы в течение времени. Вероятностные модели используются для описания случайных событий. Оптимизационные модели используются для нахождения оптимальных решений.

Какие примеры применения математических моделей в жизни?

Математические модели применяются во многих областях жизни. Например, они используются для прогнозирования погоды, моделирования климатических изменений, оптимизации производственных процессов, анализа финансовых рынков, разработки лекарственных препаратов, планирования транспортных маршрутов и многое другое. Они помогают улучшить процессы, принимать обоснованные решения и предсказывать результаты.

В экономике и финансах

Математические модели играют важную роль в экономике и финансах. Они помогают анализировать и прогнозировать различные процессы и явления, которые происходят в этих областях. Модели позволяют исследовать взаимосвязь между различными переменными, такими как цены, доходы, спрос, предложение и другие.

В экономике математические модели используются для определения оптимальных стратегий ведения бизнеса, управления ресурсами и разработки экономических политик. Они позволяют анализировать влияние различных факторов на экономические показатели и прогнозировать их изменения. Модели также помогают оценить эффективность инвестиций, определить оптимальное распределение ресурсов и разработать стратегию развития предприятий.

В финансовой сфере математические модели используются для анализа и прогнозирования финансовых рынков, оценки риска и доходности инвестиций, управления портфелем и разработки стратегий торговли на рынке ценных бумаг. Они позволяют определить оптимальное соотношение активов и рассчитать ожидаемую доходность и риск портфеля. Модели также могут использоваться для анализа влияния различных факторов, таких как изменение процентных ставок или политические события, на финансовые рынки.

Примеры применения математических моделей в экономике и финансах:

Моделирование спроса и предложения.

Оптимизация производства и распределения ресурсов.

Анализ финансовых рынков и прогнозирование их изменений.

Разработка инвестиционных стратегий и управление портфелем.

Моделирование финансовых рисков и оценка их влияния.

Видео по теме: