Создание компьютерных математических моделей: ключевые инструменты и методы

При создании компьютерных математических моделей для достижения точных и надежных результатов используются различные математические методы и алгоритмы, которые являются важными инструментами в этой области науки и технологий.

Создание компьютерных математических моделей является одной из ключевых задач в научных и инженерных областях, где необходимо проводить анализ, прогнозирование и оптимизацию различных процессов. Для решения таких задач используются математические методы и алгоритмы, которые взаимодействуют с компьютерными программами и создают математическую модель.

Математические средства играют важную роль в создании моделей. Они позволяют проектировать и оптимизировать алгоритмы работы с данными, строить графические представления и визуализации моделей, а также проводить вычисления и анализ данных.

Существует множество математических средств, используемых при создании моделей. Среди них: системы математических вычислений (например, MATLAB), языки программирования (например, Python), системы булевой алгебры и др.

Успешное создание компьютерных математических моделей невозможно без использования математических средств. Они являются неотъемлемой частью процесса создания моделей и позволяют проводить научные исследования и добиваться точных результатов.

Создание компьютерных математических моделей

Компьютерные математические модели используются для анализа сложных процессов и явлений в различных областях: физике, экономике, биологии, инженерии и многих других. Создание таких моделей является важным инструментом для исследования реальных систем и принятия соответствующих решений.

Для создания компьютерных математических моделей используются различные математические средства, такие как методы оптимизации, алгоритмы машинного обучения, статистические методы и другие. С помощью этих средств можно представить сложный процесс с помощью простых математических выражений.

Для того чтобы создать компьютерную математическую модель нужно иметь полное понимание системы, которую мы моделируем. Существует множество методов и подходов для создания математических моделей, и выбор метода зависит от типа системы, которую мы моделируем.

Создание компьютерных математических моделей требует глубоких знаний математики, программирования и теории систем. При этом нужно учитывать возможные ограничения и неопределенности, которые могут возникнуть в процессе моделирования. Корректность модели, ее точность и надежность – это основные критерии оценки качества работоспособности компьютерной математической модели.

• Математическое моделирование позволяет:
  1. Изучать и прогнозировать поведение системы в различных условиях.
  2. Анализировать влияние различных факторов на работу системы.
  3. Планировать и оптимизировать работу системы.

В целом, создание компьютерных математических моделей – это сложный, но увлекательный процесс, который позволяет получать новые знания и применять их в различных областях деятельности.

Видео по теме:

Роль математических средств

Создание компьютерных математических моделей — процесс, который невозможен без использования математических средств. Математические методы и алгоритмы являются основой для создания моделей и анализа получаемых данных.

Математические средства, такие как матрицы, векторы, функции и графы, являются неотъемлемой частью компьютерных математических моделей. Они позволяют абстрагироваться от конкретной ситуации и сосредоточиться на основных математических принципах и законах.

Одним из главных преимуществ использования математических средств является возможность получения точных результатов, а также проведения сравнительного анализа различных сценариев. Они позволяют проводить моделирование искусственных систем и предсказывать их поведение в различных условиях.

Кроме того, математические средства позволяют оптимизировать процессы проектирования и эксплуатации систем. Они позволяют проводить исследование и оптимизацию сложных систем начиная с их проектирования и заканчивая контролем за работой в реальном времени.

• Математические средства помогают:
  1. Создавать точные математические модели и компьютерные симуляции.
  2. Получать точные результаты анализа данных и моделирования.
  3. Оптимизировать процессы проектирования и эксплуатации систем.

В современном мире компьютерные математические модели используются во многих отраслях, таких как наука, технологии, экономика и бизнес. Широкое использование математических средств позволяет существенно ускорить и упростить процесс принятия решений и повысить эффективность работы во многих областях деятельности.

Компьютерные математические модели: что это?

Компьютерные математические модели — это математические модели, которые создаются на компьютере и используются для решения различных задач в науке, инженерии, экономике и других областях. Они представляют собой абстрактную математическую модель, которая описывает поведение системы в определенных условиях.

Компьютерные математические модели могут имитировать реальные процессы, свойства и явления, позволяя проводить эксперименты без затрат на проведение физических испытаний и исследований. Программное обеспечение, которое поддерживает работу с компьютерными математическими моделями, позволяет проводить анализ и прогнозирование различных сценариев развития системы в зависимости от входных данных и параметров.

Компьютерные математические модели используются для решения различных задач, таких как разработка новых материалов, управление финансовыми рисками, прогнозирование погоды, конструирование автомобилей и самолетов, расчет траекторий космических объектов и т. д.

Создание компьютерных математических моделей требует глубоких знаний в математике, информатике, физике, химии и других науках. Использование правильных математических средств и методов является необходимым условием для получения точных результатов и достижения успеха в решении задач.

Зачем нужно создавать математические модели?

Математические модели используются в различных областях науки и техники для предсказания и оптимизации поведения систем и процессов. Эти модели облегчают понимание сложных систем и помогают исследователям и инженерам принимать верные решения.

Использование математических моделей позволяет экономить время и деньги, которые могут быть затрачены на эксперименты и исследования в реальном мире. Моделирование дает возможность проверить различные сценарии и сделать прогнозы о будущем поведении системы в разных условиях.

Создание математических моделей также позволяет улучшить качество управления сложными системами. Например, моделирование экономических процессов помогает управляющим органам принимать верные решения в финансовых вопросах и предсказывать влияние различных факторов на экономику.

Наконец, математические модели используются для прогнозирования и планирования. Это особенно важно в области экологии и здравоохранения, где моделирование позволяет предсказать влияние различных факторов на окружающую среду и на здоровье людей.

В целом, математические модели играют важную роль в разных областях науки и техники, помогая ученым и инженерам понимать и управлять сложными системами, экономить время и деньги на исследования и эксперименты, а также предсказывать будущее поведение систем в различных условиях.

Сферы применения математических моделей

Математические модели широко используются в различных сферах, начиная от естественнонаучных и технических до социальных и экономических исследований.

• В физике, химии и биологии математические модели помогают описывать процессы на микро- и макроуровнях, что позволяет лучше понимать эти явления и предсказывать результаты экспериментов.
• В инженерии математические модели используются для проектирования и оптимизации различных устройств, механизмов и систем.
• В экономике и финансах математические модели широко используются для анализа рынка, прогнозирования цен и поведения потребителей.
• В социологии и политологии математические модели применяются для изучения социальных и политических процессов, структуры общества и поведения людей.

В целом, математические модели играют важную роль в научном исследовании и различных приложениях, позволяя более точно описывать и предсказывать реальные явления и процессы.

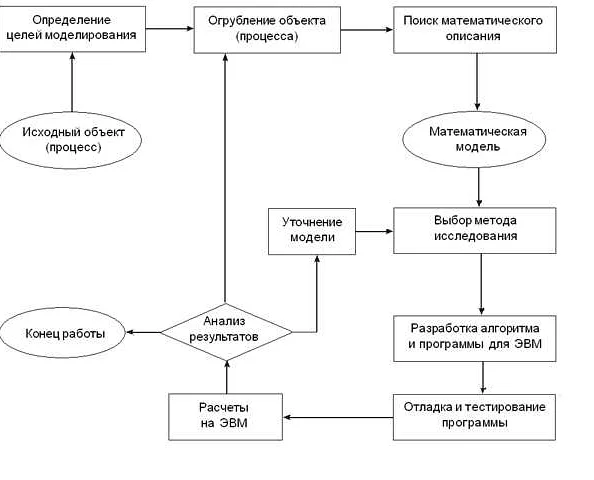
Процесс создания компьютерных математических моделей

Создание компьютерной математической модели – это сложный и многолетний процесс. Для начала необходимо понять задачу, которую необходимо решить, и на основе этого определить математическую модель. Математическая модель может быть задана в виде уравнений, графов, таблиц или других математических методов.

Далее необходимо подобрать многочисленные параметры, необходимые для создания модели. Они могут быть получены как в эксперименте, так и из исходных данных. На основе этих данных создается математическая модель, которая в дальнейшем будет использоваться в компьютерной программе.

Для создания программы используют различные математические средства, такие как языки программирования, пакеты прикладных программ, математические библиотеки и т.д. На этом этапе также важно обеспечить корректность исходного кода, чтобы избежать ошибок даже на этапе компиляции и упростить дальнейшую отладку программы.

Финальной стадией в создании компьютерной математической модели является ее тестирование. На этой стадии проверяется работоспособность программы и ее соответствие с задачей, которую необходимо решить. В процессе тестирования выявляются возможные ошибки и неточности, которые устраняются в дальнейшем.

Важность математических средств в создании моделей

Создание математических моделей – это сложный процесс, требующий высокой квалификации от их создателей. Успешное создание модели зависит от использования различных математических средств, таких как алгебра, теория графов, теория вероятностей, дифференциальные уравнения, и многие другие.

Без использования математических средств создание математической модели может стать невозможным. Эти инструменты помогают установить связи между различными переменными и улучшить точность модели. Более того, математические средства позволяют создавать модели, которые могут обрабатывать большие объемы данных и анализировать результаты, что делает их более полезными в приложениях реального мира.

Одним из важных свойств математических средств является их общая применимость. Эти инструменты могут использоваться в различных областях, таких как экономика, физика, биология, инженерия и т.д. Они позволяют создавать модели, которые могут быть применены в различных задачах и решать широкий круг проблем.

• Математические средства не только облегчают создание моделей, но и улучшают их точность и надежность. Они позволяют описывать сложные процессы и анализировать их результаты.
• Математические инструменты помогают экономить время, деньги и ресурсы, которые могут быть использованы в других областях.

В целом, использование математических средств в создании математических моделей – это необходимое условие для достижения высокой точности и правильности. И, несомненно, математические инструменты будут играть все более и более важную роль в создании будущих математических моделей.

Основные подходы к созданию компьютерных математических моделей

Создание компьютерных математических моделей является неотъемлемой частью современной науки и техники. Оно позволяет понимать сложные явления, предсказывать их поведение, оптимизировать работы и многое другое. Однако, для того чтобы создать математическую модель, необходимо выбрать подход, который наилучшим образом подойдет к решению задачи.

Одним из наиболее распространенных подходов является классический подход. Он заключается в том, что математическая модель строится на основе законов и уравнений, которые описывают явления, происходящие в реальном мире. Такой подход позволяет создать точную и надежную модель, но он требует большого количества математических знаний и способностей.

Другим подходом является эмпирический подход. Он заключается в том, что математическая модель строится на основе наблюдений и экспериментов. Такой подход позволяет создать модель, которая более точно отражает реальные явления, но он может быть менее точным и надежным.

Еще одним подходом является статистический подход. Он заключается в том, что математическая модель строится на основе статистических данных и вероятностных законов. Такой подход позволяет создать модель, которая подходит для большого количества случаев, но может быть менее точной в конкретных случаях.

Выбор подхода к созданию компьютерной математической модели зависит от типа задачи, ресурсов, которые доступны для решения этой задачи, а также от конкретных потребностей и требований пользователя. В любом случае, правильный выбор подхода позволяет создать модель, которая дает точные и достоверные результаты и помогает получить новые знания и оптимизировать работу в различных областях науки и техники.

Примеры создания математических моделей в различных сферах

Математические модели играют важную роль в многих сферах жизни. Они позволяют предсказывать поведение систем, оптимизировать процессы и принимать решения на основе точных расчетов. Вот несколько примеров, как математические модели применяются в различных областях:

• Финансы: Математические модели позволяют прогнозировать цены на акции, валюту и другие финансовые инструменты, а также определять оптимальные стратегии инвестирования и управления рисками.
• Медицина: Математические модели используются для моделирования биологических процессов, таких как рост и развитие клеток, распространение эпидемий и эффективность лекарственных препаратов.
• Транспорт: Математические модели позволяют оптимизировать расписание и маршруты общественного транспорта, прогнозировать потоки транспорта на дорогах и улучшать расход топлива.
• Экология: Математические модели используются для прогнозирования изменения климата и экосистем, оптимизации использования природных ресурсов и оценки воздействия человеческой деятельности на окружающую среду.
• Механика: Математические модели позволяют предсказывать поведение и отказы механизмов, анализировать сочетание перемещений и сил, определять долговечность конструкций и материалов.

Это только несколько примеров того, как математические модели используются в различных сферах. Все более сложные технологии и системы требуют более сложный подход при их создании и исследовании. Математические модели являются необходимым инструментом, который позволяет анализировать и оптимизировать сложные системы.

Моделирование будущих событий

Одним из главных преимуществ компьютерных математических моделей является их способность создавать прогнозы и моделировать будущие события. Это может быть полезно для многих отраслей, включая экономику, бизнес, финансы, климатологию и медицину.

Моделирование будущих событий основано на анализе и обработке данных прошлых событий. На основе этих данных можно создать математическую модель, которая будет описывать тенденции и тренды, происходящие в данной области. Эта модель может быть использована для прогнозирования будущих событий и принятия правильных решений.

Примером использования компьютерных математических моделей для прогнозирования будущих событий может служить исследование изменений климата. На основе данных о климатических изменениях последних лет можно создать математическую модель, которая позволит прогнозировать будущие изменения климата в данном регионе. Это может быть важно для разработки стратегий адаптации к неблагоприятным условиям.

Кроме того, компьютерные математические модели могут быть использованы для прогнозирования экономических и бизнес-тенденций. Они могут помочь предсказать будущие изменения курсов валют, рыночных цен и других параметров, влияющих на бизнес-процессы. Это позволяет компаниям принимать решения на основе точных данных и увеличивает вероятность успеха.

В целом, создание компьютерных математических моделей является важным инструментом для прогнозирования и моделирования будущего. Они позволяют принимать более осознанные решения, учитывая данные о прошлых и настоящих событиях, и повышают точность прогнозов. Без них многие отрасли не смогли бы оперировать на таком высоком уровне и достигать успеха.

Преимущества использования математических моделей

Уменьшение затрат на проведение экспериментов. Создание математической модели позволяет проводить виртуальные эксперименты, что значительно снижает затраты на реальные эксперименты.

Предсказание результатов. Математические модели могут помочь предсказать результаты определенных процессов и явлений, что позволяет более эффективно планировать дальнейшие действия.

Разработка новых продуктов и технологий. Создание математических моделей помогает инженерам и ученым при разработке новых продуктов и технологий, предотвращение ошибок в реальном мире и ускорение процесса разработки.

Оценка эффективности решений. Использование математических моделей позволяет оценить эффективность принимаемых решений и предсказать их последствия.

Лучшее понимание процессов и явлений. Создание математической модели позволяет более глубоко понять и исследовать процессы и явления, даже те, которые трудно изучать в реальном мире.

Вывод

Создание математических моделей является необходимым этапом для решения различных задач в науке, технике и экономике. Использование компьютерных математических моделей упрощает и ускоряет процесс исследования и предоставляет возможность проводить более точные и качественные расчеты.

Существует множество математических средств и программ, которые способствуют успешному созданию и управлению математическими моделями. Одним из наиболее популярных инструментов являются системы компьютерной алгебры, которые обеспечивают решение сложных математических задач, а также графическое представление результатов.

Однако важно помнить, что создание математической модели является только частью комплексного процесса исследования. Необходимо учитывать многие факторы, такие как качество и точность входных данных, адекватность модели, а также необходимость регулярного ее обновления и корректировки в соответствии с полученными результатами.

Таким образом, создание компьютерных математических моделей имеет огромный потенциал и может быть успешно использовано в различных областях знания. Однако для достижения наилучших результатов необходимо учитывать все аспекты процесса исследования и быть готовым к постоянному усовершенствованию и корректировке созданных моделей.

Вопрос-ответ:

Какой математический пакет лучше использовать для создания математических моделей?

Выбор математического пакета зависит от конкретной задачи и предпочтений пользователя. Например, MATLAB часто используют для численных расчетов, а Mathcad — для работы с символьными выражениями. Но в целом, важно выбрать пакет, который поддерживает необходимые функции и удобен в использовании.

Какие проблемы могут возникнуть при создании компьютерной математической модели?

При создании математической модели могут возникнуть проблемы с недостаточностью данных о предметной области, неверным выбором математических методов или ошибками в реализации алгоритмов. Также может быть проблема с оптимизацией параметров модели.

Какие математические методы чаще всего используются при создании компьютерных математических моделей?

Часто используются численные методы, такие как метод конечных разностей, метод конечных элементов и методы Монте-Карло. Также применяются символьные методы, например, методы аналитического решения дифференциальных уравнений.

Каким образом можно убедиться в корректности математической модели?

Для проверки корректности модели могут быть использованы тестовые примеры или сравнение результатов моделирования с экспериментальными данными. Также можно провести чувствительностный анализ — изменять параметры модели и наблюдать, как это влияет на результат.

Можно ли использовать математические модели для прогнозирования будущих событий и результатов?

Да, математические модели могут использоваться для прогнозирования будущих событий и результатов. Однако, такие прогнозы, как правило, сопряжены с высокой степенью неопределенности и могут быть неточными.

Каковы преимущества создания компьютерных математических моделей по сравнению с использованием аналитических методов?

Создание математических моделей на компьютере позволяет снизить затраты на проведение эксперимента, а также улучшить точность результатов. Кроме того, компьютерные модели позволяют учитывать больший диапазон входных данных и оценивать более сложные процессы.

Какие примеры применения компьютерных математических моделей в науке и технологиях вы можете привести?

Примерами применения компьютерных математических моделей в науке и технологиях могут служить: прогнозирование погоды, проектирование летательных аппаратов, оптимизация ракетных двигателей, моделирование движения жидкостей и газов, анализ динамических систем и многое другое.