Математическое моделирование: что это и зачем оно нужно?

Математическое моделирование – это процесс создания математических моделей для изучения, анализа и оптимизации различных процессов и явлений в науке, технике и экономике. В статье вы узнаете, как работает математическое моделирование, какие методы и инструменты применяются для создания моделей и какие задачи решаются с помощью такого подхода.

Математическое моделирование — это метод, который использует математические теории и компьютерные алгоритмы для создания упрощенных и абстрактных моделей сложных систем, процессов и явлений. Этот метод позволяет улучшить наше понимание сложных систем и предсказать их поведение.

Математическое моделирование может быть применено в различных областях, включая науку, технологию, экономику, медицину и другие. Например, математические модели используются для предсказания погоды, оптимизации производства, оценки рисков и диагностики заболеваний.

Важным преимуществом математического моделирования является его способность представлять реальную систему с высокой точностью, учитывая различные факторы, влияющие на ее поведение. Это в свою очередь позволяет предвидеть, как изменения в системе могут повлиять на ее работу, и определить оптимальные условия для достижения поставленных целей.

Вместе с тем, математическое моделирование имеет свои ограничения и недостатки, такие как сложность построения модели и необходимость наличия точных данных для ее создания. Однако, тем не менее, этот метод остается важным инструментом для решения различных задач в науке и индустрии.

Определение математического моделирования

Математическое моделирование – это процесс построения абстрактных математических моделей объектов, систем или процессов с целью описания и изучения их свойств и поведения. Модель – это упрощенное, формализованное отображение искомой системы или явления в математической форме, позволяющее проводить анализ свойств и поведения системы и прогнозировать ее будущее.

Математическое моделирование может применяться в разных областях знаний, включая физику, химию, биологию, экономику, социологию и другие науки. В каждой области математическое моделирование имеет свои особенности и требования к точности и сложности моделей, но в целом, все модели строятся на основе одних и тех же математических закономерностей.

Основой математического моделирования является математический аппарат – система математических понятий и методов, которые используются при построении моделей. В зависимости от сложности и специфики моделей может применяться различный математический аппарат, включая дифференциальные уравнения, вероятностную теорию, теорию графов, теорию автоматов и другие.

• Математическое моделирование позволяет проводить численные эксперименты, которые были бы невозможны в реальности из-за высоких затрат времени, сил и денег. При этом моделирование может дать более точные результаты, чем эксперименты в реальной среде из-за возможности контроля всех параметров модели.
• Моделирование также позволяет прогнозировать проблемы в работе системы или предсказывать ее поведение в сложных ситуациях. Например, математическое моделирование распространения эпидемии или моделирование трафика на дорогах позволяет определить оптимальные стратегии управления.

История развития математического моделирования

Математическое моделирование имеет давнюю историю, начинающуюся с древних греков, которые использовали геометрические модели для решения задач физики и механики. В сочетании с математическим анализом, моделирование позволило развивать теорию движения, включая теорию обратного движения планет и гравитационный закон.

В средние века и в период Возрождения математическая модель развивалась в основном в области науки о земле и астрономии. Например, астрономия использовала моделирование для предсказания движения планет, а наука о земле — для моделирования извержения вулканов.

В 20-м веке математическое моделирование стало важной частью научных исследований во многих областях, включая физику, химию, биологию, экономику и социологию. Развитие компьютеров и численных методов расширил возможности математического моделирования, что привело к росту его применения в промышленности и технике.

Сегодня математическое моделирование является неотъемлемой частью научных и инженерных исследований, позволяя создавать сложные системы, предсказывать их поведение, оптимизировать параметры и решать разнообразные задачи во многих областях человеческой деятельности.

Примеры использования математического моделирования в бизнесе

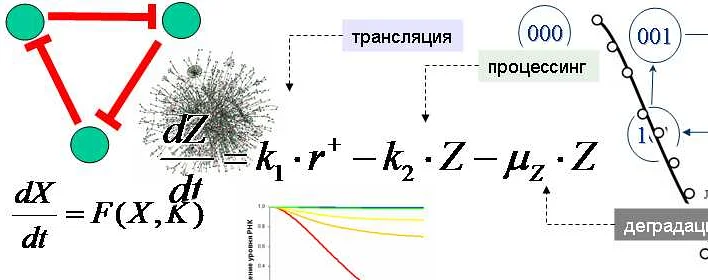
Математическое моделирование является важным инструментом при принятии решений в бизнесе. Применение математических методов позволяет уменьшить риски и оптимизировать процессы в различных сферах деятельности.

Один из наиболее распространенных примеров использования математического моделирования в бизнесе — это прогнозирование спроса на товары и услуги. С помощью математических методов можно прогнозировать, как изменится спрос на продукцию компании в зависимости от различных факторов, таких как экономические показатели, погода, маркетинговые кампании и т.д. Это позволяет с точностью предсказать, сколько товаров необходимо произвести и сколько их нужно реализовать, а также управлять запасами.

Еще один пример использования математического моделирования в бизнесе — это оптимизация логистических процессов. С помощью математических методов можно определить оптимальный маршрут доставки товаров, учитывая множество факторов, таких как расстояние между пунктами назначения, стоимость топлива, время на доставку и многие другие. Это помогает снизить затраты на логистику и оптимизировать процессы внутри компании.

Кроме того, математическое моделирование имеет широкое применение в финансовой сфере, например, при расчете рисков при инвестировании, определении оптимального состава инвестиционного портфеля, анализе финансовых показателей и т.д. Это позволяет управлять финансовыми активами и минимизировать риски для компании.

Таким образом, математическое моделирование является важным инструментом для бизнеса. С его помощью можно оптимизировать процессы, управлять рисками и принимать оптимальные решения, что в свою очередь способствует росту прибыли и стабильности компании.

Процесс математического моделирования

Математическое моделирование — это процесс создания формальной математической модели или моделей с целью изучения системы или процесса. Процесс создания модели называется моделированием, а модель — абстрактной математической репрезентацией реального процесса.

При создании математической модели нужно определить все факторы, оказывающие влияние на исследуемый процесс или систему. Затем необходимо разработать методы, которые позволят определить, как изменения в одном или нескольких факторах повлияют на процесс. Например, при моделировании экономического процесса необходимо учитывать множество факторов, таких как инфляция, процентные ставки, безработица и т.д.

В процессе создания математической модели или системы уравнений, которые описывают данный процесс, необходимо определить начальные данные для всех факторов. Затем эти данные вводятся в систему уравнений, решаются и анализируются. Результаты анализа могут дать важные выводы о том, как работает процесс.

Однако математическое моделирование не настолько просто, как это кажется. Создание математической модели может потребовать много времени и ресурсов, и часто бывает необходимо вносить изменения в модель в процессе ее разработки. Кроме того, результаты моделирования могут быть не полностью точными, так как любая модель является упрощением реальности. Поэтому важно быть осторожным при интерпретации результатов моделирования и использовать их только в сочетании с другими методами исследования.

Типы математических моделей

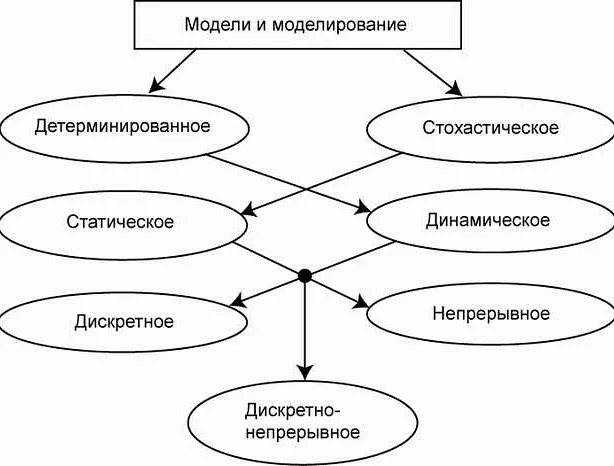
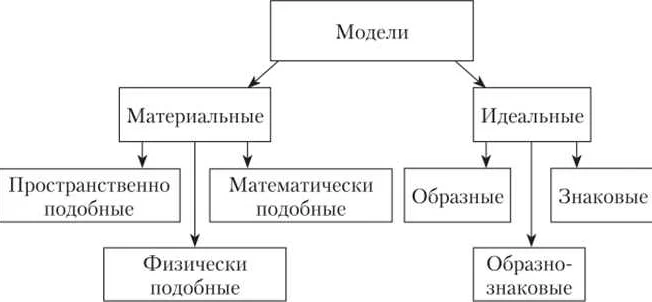
Математические модели – это абстрактные системы, созданные для описания процессов и объектов с высокой точностью. Существует несколько типов математических моделей, каждый из которых используется в определенных условиях и областях знаний.

Одним из типов математических моделей является аналитическая модель. Эта модель основана на решении уравнений и формул, которые полностью описывают процесс или объект. Аналитические модели используются, когда нужно получить точное решение задачи. Однако, для сложных процессов они могут быть излишне сложными и неэффективными.

Статистические модели – это другой тип математических моделей. Эти модели используют статистические методы анализа данных, которые позволяют сделать выводы о процессе или объекте. Статистические модели основаны на вероятностных распределениях и допущениях. Они используются, когда точные решения не принципиальны, а важно только получить общее представление о процессе.

Компьютерные модели – это наиболее широко используемый тип математических моделей. Они основаны на алгоритмическом описании и позволяют смоделировать процесс или объект в условиях, приближенных к реальным. Компьютерные модели могут быть как аналитическими, так и статистическими.

Каждый из типов математических моделей имеет свои преимущества и недостатки. Выбор конкретного типа зависит от поставленной задачи и доступных ресурсов.

Основные принципы математического моделирования

Математическое моделирование представляет собой методологический подход к изучению и прогнозированию различных явлений и процессов с помощью математических моделей.

Основные принципы математического моделирования:

1. Выбор моделируемой системы и ее свойств. Первым шагом в математическом моделировании является выбор системы, которую мы хотим исследовать. Далее мы определяем ее свойства, которые будут включены в модель.
2. Построение математической модели. На этом этапе создается математическая модель, которая описывает поведение выбранной системы. Она может быть представлена в виде уравнений, графиков, таблиц и других математических инструментов.
3. Моделирование и анализ. Полученную модель необходимо проверить на правильность и адекватность. На данном этапе происходит моделирование поведения системы в различных условиях и анализ полученных результатов.
4. Верификация и валидация модели. Модель не может быть точной копией реальной системы, поэтому ее необходимо проверять на соответствие и достоверность. Этот этап называется верификацией и валидацией модели.
5. Прогнозирование и оптимизация. Полученная модель может быть использована для прогнозирования поведения системы в различных условиях и оптимизации ее работы.

Математическое моделирование является важным инструментом в научных и технических исследованиях и позволяет получить новые знания и улучшить существующие технологии.

Преимущества и недостатки использования математического моделирования

Преимущества:

• Позволяет получить более точное представление о процессах и явлениях, чем эксперименты на реальных объектах.
• Позволяет проводить исследования в условиях, которые невозможно создать на практике, например, из-за высоких экспериментальных затрат или опасности для жизни и здоровья людей.
• Позволяет экономить время и ресурсы на проведении экспериментов.
• Позволяет быстро изменять параметры модели и проверять различные гипотезы без необходимости проводить новые эксперименты.

Недостатки:

• Модели могут быть неточными из-за неполного или неверного описания реальности, ошибок в данных и т.д.
• Иногда невозможно создать математическую модель для сложных систем, которые имеют множество взаимодействующих факторов.
• Моделирование может приводить к потере информации о некоторых нюансах реальных процессов, которые не учитываются в модели.
• Создание и разработка математических моделей требует знаний и навыков в математике, информатике и физике, что может быть сложным для неподготовленных специалистов.

Таким образом, математическое моделирование имеет как преимущества, так и недостатки, которые нужно учитывать при его использовании. Однако, несмотря на ограничения, моделирование является важным инструментом для исследования реальности и позволяет получить более точное представление о процессах и явлениях в мире.

Распространенные проблемы при математическом моделировании

При математическом моделировании могут возникать различные проблемы, связанные с выбором математической модели, недостаточностью данных, неточностью формулировки условий задачи и другими факторами. Рассмотрим некоторые из распространенных проблем.

1. Выбор математической модели. Один из наиболее важных аспектов моделирования заключается в выборе подходящей модели для решения конкретной задачи. Ошибки в выборе модели могут привести к некорректным результатам или нарушению логики решения задачи. Необходимо учитывать также, что одна и та же модель может давать различные результаты в зависимости от условий задачи.

2. Недостаточность данных. Для построения адекватной математической модели требуется наличие достаточного количества данных. Однако, в ряде случаев, такие данные могут быть недоступны или не полны. Недостаточность данных может привести к неточным результатам и снижению точности модели.

3. Неточность формулировки задачи. Некорректность формулировки задачи может привести к неправильному выбору математической модели и к неверным результатам. Важно ясно определить все условия задачи и учесть все факторы, которые могут повлиять на результат.

4. Оценка рисков и ошибок. При моделировании необходимо учитывать возможные ошибки и риски. Например, может возникнуть недопустимое поведение модели при определенных условиях. Важно проводить анализ ошибок и рисков и разрабатывать стратегии для их устранения.

5. Ограничения вычислительной мощности. Математические модели могут быть очень сложными и требовательными к вычислительным ресурсам. В связи с этим возникает проблема нехватки вычислительных ресурсов и необходимости использования специализированных методов решения задач.

Сравнение математического моделирования с другими методами прогнозирования

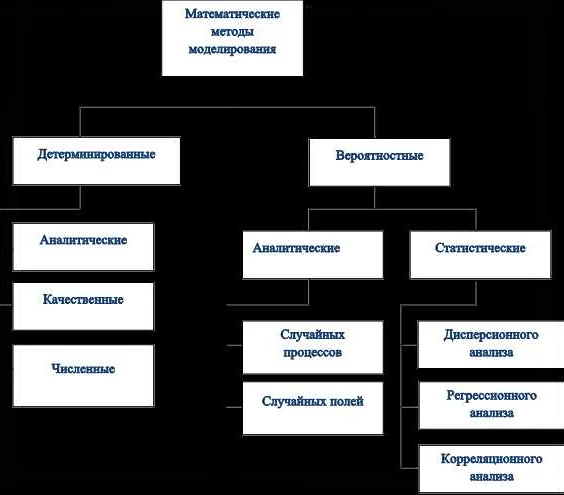
Математическое моделирование — это метод прогнозирования, который использует математические модели для оценки будущих событий. Этот метод является относительно точным и может быть использован в различных областях, таких как экономика, физика, биология и многих других.

С другой стороны, есть другие методы прогнозирования, такие как экспертные оценки, опросы и статистические методы, которые могут использоваться для прогнозирования будущих событий. Экспертные оценки могут быть нестабильными и сильно зависеть от мнения эксперта, а опросы могут быть искажены из-за неправильных ответов или недостаточной выборки.

Статистические методы, такие как регрессионный анализ и кластерный анализ, могут быть использованы для прогнозирования будущих событий. Однако они могут быть менее точными, чем математическое моделирование, и обычно применяются только в определенных областях, таких как маркетинг и социология.

Из этих методов прогнозирования математическое моделирование может быть наиболее точным, если вы сможете создать правильную модель для предсказания будущих событий. Однако каждый метод может иметь свои преимущества и недостатки, в зависимости от области применения.

Итог: В целом, математическое моделирование является точным и широко используемым методом прогнозирования, который может быть применен в различных областях. В то же время, другие методы, такие как экспертные оценки и статистические методы, могут быть полезны в определенных ситуациях, в зависимости от области применения и доступных данных.

Вопрос-ответ:

Что такое математическое моделирование?

Математическое моделирование — это процесс построения математической модели, которая описывает поведение системы.

Какую роль играет математическое моделирование в науке?

Математическое моделирование помогает научным исследователям понять и предсказать поведение объектов и систем в разных сферах науки, таких как физика, биология, экономика, инженерия и т.д.

Какие типы математических моделей существуют?

Существует множество типов математических моделей: дискретные, непрерывные, детерминированные, стохастические и т.д. Каждый тип модели выбирается в зависимости от задачи и свойств системы, которую нужно исследовать.

Каковы основные этапы построения математической модели?

Основные этапы построения математической модели: формулирование задачи, сбор данных, выбор типа модели, разработка математических формул, решение уравнений и интерпретация результатов.

Какие преимущества дает математическое моделирование в бизнесе?

Математическое моделирование позволяет бизнесу повысить эффективность и оптимизировать процессы, такие как управление запасами, оптимизация цепочки поставок, прогнозирование продаж и т.д. Также моделирование помогает принимать более обоснованные решения, минимизировать риски и улучшить конкурентоспособность.

Какими программными инструментами можно воспользоваться для математического моделирования?

Для математического моделирования существует множество программных инструментов: MATLAB, Mathematica, Maple, R, Python и т.д. Каждый инструмент имеет свои преимущества и недостатки, и выбор программы зависит от задачи и доступных ресурсов.

Какие вызовы существуют в математическом моделировании?

В математическом моделировании существуют различные вызовы, такие как сложность моделирования системы, неопределенность данных, потребность в высокоточных вычислениях и т.д. Решение этих вызовов требует совершенствования методов и инструментов математического моделирования.

Роль математического моделирования в науке и технике

Математическое моделирование играет важную роль в науке и технике. С помощью математических моделей ученые и инженеры могут анализировать, предсказывать и оптимизировать различные процессы и явления.

Это особенно важно в тех случаях, когда экспериментальное исследование процесса становится слишком сложным, дорогостоящим и времязатратным. В таких случаях, создание математической модели и её компьютерное моделирование может значительно сократить время и затраты, а также дать более точные результаты.

Математическое моделирование используется в широком спектре областей: от физики, химии и биологии до экономики, социологии и психологии. Оно применяется в проектировании новых технологий, устройств и механизмов, предсказании погоды, моделировании климатических изменений, и многих других областях.

Одним из ключевых преимуществ математического моделирования является возможность проводить виртуальные эксперименты, которые могут быть опасными в реальности. Например, математическое моделирование используется в разработке новых лекарств, что позволяет проводить исследования, которые бы были невозможны при работе с реальными людьми.

В целом можно сказать, что математическое моделирование является инструментом, который позволяет ученым и инженерам лучше понимать и оперировать с различными явлениями и процессами.

Видео по теме: