Что такое математическое моделирование в музыке

Математическое моделирование в музыке — это процесс использования математических методов и алгоритмов для создания, анализа и прогнозирования музыкальных структур, звуков и композиций. Узнайте, как математическое моделирование может быть применено в музыке и какие преимущества оно может предоставить для композиторов и музыкантов.

Математика и музыка — две области, которые кажутся на первый взгляд несовместимыми. Одна из них строится на точных расчетах, формулах и числах, а другая — на эмоциях, восприятии и творческом потенциале. Однако, на самом деле, существует глубокая связь между этими двумя предметами. Математическое моделирование в музыке открывает новые пути для композиторов, исполнителей и исследователей, позволяя им создавать и анализировать музыкальные произведения с помощью математических методов и алгоритмов.

Основным принципом математического моделирования в музыке является перевод музыкальных элементов в числовую форму и их дальнейшая обработка с использованием математических операций. Таким образом, музыка становится объектом исследования, который может быть анализирован, преобразован и создан с помощью формул и алгоритмов. Это позволяет композиторам экспериментировать с различными музыкальными структурами, темпами, гармониями и т.д., предсказывать результаты и оценивать эффект от изменений в музыкальной композиции.

«Математическое моделирование в музыке не только помогает композиторам разрабатывать новые музыкальные идеи и концепции, но и способствует исследованию музыкальной теории и психоакустических явлений.»

Применение математического моделирования в музыке может быть очень широким. Оно включает в себя разработку компьютерных программ и алгоритмов для создания музыки, анализа музыкальных произведений, прогнозирования и классификации музыкальных жанров, моделирования звуковых волн и многое другое. Математика позволяет нам лучше понять музыку, раскрыть ее внутренние законы и принципы, а также открыть новые возможности для развития и инноваций в музыкальной индустрии.

Что такое математическое моделирование в музыке?

Математическое моделирование в музыке основано на представлении музыки в виде математических объектов и формул, которые позволяют анализировать и предсказывать ее свойства и поведение. Например, можно использовать математические модели для изучения и определения аккордов, мелодических структур, темпа и тоника музыкальных произведений.

Кроме того, математическое моделирование в музыке позволяет создавать новые музыкальные композиции и звуковые эффекты. Используя математические алгоритмы и модели, композиторы и звукорежиссеры могут создавать уникальные звуковые текстуры, ритмические паттерны и гармонические прогрессии.

Также математическое моделирование в музыке имеет практическое применение в области музыкальных инструментов и записи звука. С помощью математических моделей можно улучшить звукосниматели, усилители и другое аудиооборудование, а также создавать новые методы обработки и сжатия звука.

Важно отметить, что математическое моделирование в музыке не заменяет творческого процесса и человеческого восприятия музыки. Оно служит инструментом для исследования и расширения возможностей музыкального искусства, а также для создания новых и уникальных музыкальных произведений.

Видео по теме:

Основные принципы математического моделирования

Основные принципы математического моделирования включают:

1. Выбор модельных переменных и параметров. При построении математической модели необходимо определить, какие переменные и параметры будут участвовать в моделировании. Это может быть, например, частота звука, амплитуда звука, длительность ноты и т.д.
2. Формулирование математических уравнений. Для описания взаимосвязей между переменными и параметрами в модели необходимо определить математические уравнения. Это могут быть уравнения дифференциальных или разностных, алгебраические уравнения и т.д.
3. Решение математических уравнений. После формулировки уравнений необходимо решить их, чтобы получить численные значения переменных и параметров модели. Для этого применяются различные методы численного решения уравнений, такие как метод Эйлера, метод Рунге-Кутты и другие.
4. Проверка и анализ модели. После получения численных значений переменных и параметров модели необходимо проверить и проанализировать модель. Это может включать сравнение результатов моделирования с экспериментальными данными или сравнение моделей с разными параметрами, чтобы выявить особенности модели и ее соответствие реальным явлениям.
5. Интерпретация результатов. Полученные результаты моделирования необходимо интерпретировать и извлечь из них практические выводы. Это может быть, например, анализ качества звучания музыкальных инструментов или оптимизация параметров звуковых эффектов.

Основные принципы математического моделирования являются ключевыми для успешного применения математических методов в изучении и анализе музыкальных явлений. Они позволяют создавать точные и эффективные модели, которые могут быть использованы для решения различных задач в области музыки.

История использования математического моделирования в музыке

В Древней Греции математики и философы изучали связь между числами и музыкой. Они обнаружили, что музыкальные гармонии могут быть описаны с помощью математических отношений. Например, равномерное деление октавы на 12 полутонов было предложено в греческой традиции, что впоследствии стало основой для настройки музыкальных инструментов.

В средние века и эпоху Ренессанса математическое моделирование в музыке продолжило развиваться. Знаменитый итальянский математик Леонардо Фибоначчи исследовал числовые последовательности, которые сейчас называются его именем, и которые имеют связь с музыкой. Фибоначчи открыл, что ряд чисел, известный как «фибоначчиева последовательность», может быть использован для создания гармонических пропорций.

В 18 и 19 веках математическое моделирование в музыке стало особенно важным. Физик и математик Эрнст Хенрих Вебер разработал теорию гармонического анализа, которая позволяет описывать сложные звуковые волны с помощью синусоидальных функций. Эта теория стала основой для развития современной музыкальной аккомпанементальной техники.

С развитием компьютерной технологии и электронной музыки в 20 веке математическое моделирование стало неотъемлемой частью музыкального творчества. Использование компьютерных программ позволяет музыкантам и композиторам создавать сложные звуковые текстуры и эффекты с помощью математических алгоритмов.

Сегодня в музыке математическое моделирование продолжает развиваться, открывая новые возможности для музыкантов и композиторов. Оно используется не только для создания новых звуковых эффектов, но также для анализа музыкальных произведений и изучения музыкальных стилей. Математическое моделирование в музыке помогает расширить границы музыкального искусства и открывает новые перспективы для творчества.

Вопрос-ответ:

Какие принципы математического моделирования применяются в музыке?

В музыке применяются различные принципы математического моделирования, такие как акустическое моделирование, моделирование звуковых волн, а также статистическое моделирование для анализа и синтеза музыкальных композиций.

Как математическое моделирование помогает в создании музыки?

Математическое моделирование помогает в создании музыки, позволяя анализировать и синтезировать звуки, оптимизировать звучание инструментов, создавать новые звуковые эффекты и композиции. Моделирование позволяет музыкантам и композиторам экспериментировать с различными звуковыми параметрами и прогнозировать результаты.

Какие результаты можно достичь с помощью математического моделирования в музыке?

С помощью математического моделирования в музыке можно достичь различных результатов. Например, можно создать реалистичные модели звуковых инструментов или эффектов, оптимизировать звучание композиций, предсказать воздействие различных параметров на звук и многое другое. Моделирование также позволяет исследовать музыку с научной точки зрения и расширить возможности музыкального творчества.

Какие инструменты используются для математического моделирования звука?

Для математического моделирования звука используются различные инструменты, включая программное обеспечение для акустического моделирования, компьютерные алгоритмы для анализа и синтеза звука, математические модели инструментов и звуковых эффектов. Кроме того, специалисты в области звука и музыки используют математические методы и приборы для измерения и записи звуковых параметров.

Какие примеры применения математического моделирования в музыке вы можете привести?

Примеры применения математического моделирования в музыке включают создание компьютерных программ для генерации и обработки звука, разработку инновационных инструментов и эффектов, анализ и классификацию музыкальных композиций, а также оптимизацию звучания легендарных музыкальных инструментов. Математическое моделирование также применяется для исследования влияния музыки на человека и развития новых подходов к композиции и исполнению музыки.

Какие принципы лежат в основе математического моделирования в музыке?

Математическое моделирование в музыке основано на принципе анализа и синтеза звуковых сигналов. Анализ позволяет разбить звук на составляющие частоты и амплитуды, а синтез позволяет создавать новые звуки путем комбинирования этих составляющих. Также в математическом моделировании используются принципы трансформации звука, такие как изменение громкости, темпа, тональности и т.д.

Каким образом математическое моделирование применяется в музыке?

Математическое моделирование применяется в музыке для создания новых звуков, аранжировки музыкальных композиций, создания эффектов и обработки звука. Например, с помощью математического моделирования можно создать звуковой эффект эхо или реверберации, изменить тональность или темп музыкальной композиции, добавить различные фильтры и эффекты. Также математическое моделирование позволяет создавать новые инструменты и синтезаторы, которые могут имитировать звуки реальных музыкальных инструментов или создавать уникальные звуки, которые невозможно получить с помощью обычных инструментов.

Применение математического моделирования в музыке

Музыка и математика имеют долгую историю взаимосвязи. Строгие математические принципы используются в музыке для создания гармонии, мелодии и ритма. Однако с развитием компьютерных технологий возникла возможность применения математического моделирования для создания новых музыкальных произведений и исследования музыкальных явлений.

Математическое моделирование в музыке позволяет анализировать звуковые структуры, прогнозировать их характеристики и создавать новые звучания. Оно основано на представлении музыки в виде математических объектов и уравнений. Таким образом, математическое моделирование помогает понять и объяснить музыкальные явления через логические и формальные методы.

Применение математического моделирования в музыке находит свое применение в нескольких областях. Во-первых, оно позволяет создавать компьютерные программы для композиции музыки. Математическое моделирование помогает автоматизировать процесс создания музыки, что значительно расширяет возможности композиторов и музыкантов.

Во-вторых, математическое моделирование используется для создания звуковых эффектов и обработки звука. С помощью математических алгоритмов можно изменять звуковые сигналы, добавлять эффекты эхо, реверберации, фильтрацию и т.д. Это позволяет создавать новые звуковые текстуры и экспериментировать с звуками.

В-третьих, математическое моделирование в музыке используется для изучения и анализа музыкальных структур и форм. Математические методы позволяют исследовать гармонические и мелодические прогрессии, ритмические структуры и другие аспекты музыки. Это помогает раскрыть тайны музыкального языка и создать новые теории искусства.

Таким образом, применение математического моделирования в музыке не только обогащает творческий процесс, но и позволяет обнаружить новые аспекты и закономерности в музыкальном искусстве. Оно дает возможность создавать музыкальные произведения, которые ранее были недоступны, и исследовать музыкальные явления с новых, математических позиций.

Математическое моделирование в композиции и аранжировке

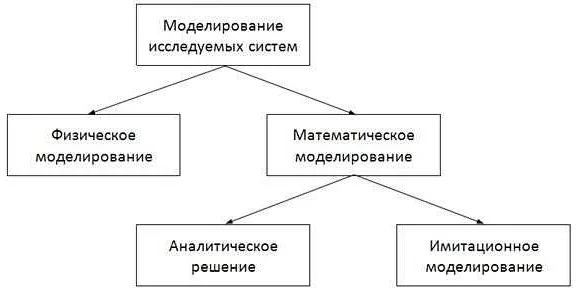
Математическое моделирование играет важную роль в композиции и аранжировке музыки. Оно позволяет композиторам и аранжировщикам использовать математические принципы и модели для создания и улучшения музыкальных произведений.

Одним из основных применений математического моделирования в композиции является создание музыкальных структур и форм. Математические модели позволяют определить последовательность аккордов, мелодические повторы и вариации, а также форму композиции в целом. Это помогает композиторам создавать музыку с определенной логикой и структурой.

Кроме того, математическое моделирование может быть использовано для аранжировки музыки. Например, аранжировщик может использовать математические модели для определения расположения инструментов в пространстве звуковой сцены, управления громкостью и панорамой звуков, а также для создания эффектов и звуковых обработок. Это позволяет достичь оптимального звучания и эмоционального воздействия на слушателя.

Кроме того, математическое моделирование может быть использовано для создания новых звуков и инструментов. Математические модели позволяют аранжировщикам и композиторам экспериментировать с различными звуковыми характеристиками, изменять их параметры и создавать уникальные звуки. Таким образом, математическое моделирование стимулирует творческий процесс и помогает создавать инновационную музыку.

В целом, математическое моделирование играет важную роль в композиции и аранжировке музыки, позволяя выразить идеи композитора и аранжировщика в математической форме, а также улучшить звучание и эмоциональное воздействие музыкальных произведений.

Роль математического моделирования в звукозаписи и синтезе звука

Одной из основных задач математического моделирования в звукозаписи является точная репрезентация звуковых сигналов. Звук может быть представлен в виде числовой последовательности, где каждое значение представляет амплитуду звука в определенный момент времени. Математические модели позволяют точно описать эту последовательность и воспроизвести звук с высокой степенью точности.

В синтезе звука математическое моделирование используется для создания новых звуков и обработки уже существующих. С помощью математических алгоритмов можно моделировать различные аспекты звука, такие как его форма, спектральный состав, атака и затухание. Это позволяет создавать реалистичные звуки различных инструментов и эффектов.

Математическое моделирование также применяется для анализа и обработки звуковых сигналов. С помощью математических методов можно выявлять особенности звуков, такие как гармоники, ритмические структуры и частотные характеристики. Это помогает профессионалам в области звукозаписи и звуковой инженерии улучшить качество звукозаписей и сделать их более привлекательными для слушателя.

Кроме того, математическое моделирование позволяет создавать различные эффекты и обработки звука, такие как эхо, реверберация, фазовые сдвиги и другие. С помощью математических алгоритмов можно точно контролировать эти эффекты и создавать новые звуковые пространства.

В заключение, можно сказать, что математическое моделирование играет важную роль в звукозаписи и синтезе звука, позволяя создавать и обрабатывать звуки с высокой точностью и контролем. Благодаря математическим моделям звук можно анализировать, обрабатывать и создавать новые звуки и эффекты, делая музыку более интересной и качественной.

Математическое моделирование в анализе и классификации музыки

Математическое моделирование имеет важное значение в анализе и классификации музыки. Математические модели позволяют нам по-новому взглянуть на музыкальные произведения, анализировать их структуру и свойства, а также классифицировать их по различным признакам. В этой статье мы рассмотрим некоторые принципы и применение математического моделирования в контексте музыки.

Анализ музыкальной структуры

Одной из важных задач в анализе музыки является определение ее структуры. Математическое моделирование позволяет нам выявлять и анализировать различные элементы и связи в музыкальном произведении. Например, можно использовать математические модели для выявления повторяющихся фраз, аккордов, мотивов и тем, а также для анализа гармонической структуры и ритмических характеристик.

Классификация музыкальных жанров

Математическое моделирование также может быть использовано для классификации музыкальных произведений по жанрам. Математические модели позволяют нам выявлять и анализировать характерные признаки каждого жанра и использовать их для построения алгоритмов классификации. Например, можно использовать математические модели для анализа спектра звуковых сигналов, темпа, мелодии и других акустических характеристик, чтобы классифицировать музыку по жанрам, таким как рок, джаз, классика, электронная музыка и т. д.

Генерация музыки

Математические модели также могут быть использованы для генерации новой музыки. Создание математических моделей, основанных на структуре и свойствах существующих музыкальных произведений, позволяет нам создавать новые музыкальные композиции. Математическое моделирование может быть использовано для создания новых мелодий, аккордов, ритмов и других элементов музыки, а также для экспериментов с гармонией и структурой.

В заключение, математическое моделирование играет важную роль в анализе и классификации музыки. Оно позволяет нам лучше понять музыкальные произведения, их структуру и свойства, а также классифицировать и генерировать новую музыку. Использование математических моделей в музыке открывает перед нами новые возможности и перспективы исследования и творчества.

Математическое моделирование в исследовании аккордов и гармонии

Одной из основных задач математического моделирования аккордов и гармонии является анализ частотных характеристик звуковых волн. Музыкальные аккорды состоят из нескольких звуков, которые имеют определенные частоты. Используя математические методы, можно определить эти частоты и визуализировать их в виде спектрограммы или графика.

Другой важной задачей является моделирование гармонии. Гармония в музыке — это сочетание разных аккордов и звуков, которые звучат вместе. Математическое моделирование позволяет исследовать, какие аккорды гармонично сочетаются друг с другом и создают определенные эмоциональные эффекты.

Математическое моделирование также позволяет анализировать изменения аккордов и гармонии во времени. Это помогает понять, как музыка развивается и создает определенное настроение у слушателя.

Использование математического моделирования в исследовании аккордов и гармонии помогает расширить наши знания о музыке и открыть новые возможности для творчества. Это позволяет композиторам и музыкантам создавать новые музыкальные произведения, основываясь на математических принципах и закономерностях.