Математика и музыка: что их объединяет и как это работает

Узнайте, как математика и музыка тесно связаны друг с другом. Почему ноты и аккорды имеют определенные числовые значения? Как математические законы влияют на гармонию и ритм композиций? Как создание музыки может помочь в изучении математики? Ответы на эти и другие вопросы вы найдете в нашей статье.

Какая связь может быть между математикой и музыкой? На первый взгляд, эти две области знаний не имеют между собой ничего общего. Однако история знает примеры того, как великие композиторы оказывались гениальными математиками, а математики, в свою очередь, восстанавливали музыкальные произведения через математические законы.

Сегодня многие ученые исследуют параллели между математикой и музыкой. Они замечают, что музыкальные произведения, такие как сонаты и фуги, часто строятся по строгим математическим законам и принципам. Поэтому музыка может быть интерпретирована как математический объект.

Но не только музыка соответствует математическому закону. Математические теории могут быть применены к вычислению звуковых параметров музыкальных произведений. Например, ритмическая структура песен может быть описана в терминах математического времени и полиритмии.

Таким образом, математика и музыка имеют глубокую взаимосвязь, что может помочь как композиторам, так и математикам в их творчестве и исследованиях.

Исторические корни соприкосновения математики и музыки

Взаимосвязь музыки и математики имеет давнюю историю, начиная с древних греков. В эпоху средневековья математики использовали знания о музыке, чтобы изучать гармонические отношения звуков и переводить музыкальные произведения в новые ключи и тональности.

В Ренессансе возник новый интерес к изучению музыки, основанный на математических подходах. Итальянский философ и математик Пьеро делла Франческа проводил параллели между музыкой и геометрией, отмечая, что звуковые вибрации могут быть представлены графически.

В XVIII веке немецкий композитор Йоганн Себастьян Бах считал, что музыка и математика тесно связаны. Бах использовал математические принципы, такие как числовые соотношения и гармонические закономерности, для создания своих музыкальных произведений.

В XX веке математические методы начали применяться в диджитал-музыке, чтобы создавать новые звуковые эффекты. Также математика находит свое применение в создании современных музыкальных инструментов, таких как электронные синтезаторы и компьютерные программы.

В итоге, можно сказать, что музыка и математика имеют множество общих точек соприкосновения. Оба предмета используют логический подход и изучают отношения между элементами. Изучение музыки может помочь в изучении математики, а знания математики могут сделать изучение музыки более логическим и понятным.

Видео по теме:

Музыка и математика: аналогии в основах системы

Внешне музыка и математика являются двумя совершенно разными науками. Однако при более тщательном анализе оказывается, что между ними имеются близкие параллели, особенно в основах системы.

Основополагающими элементами в музыке являются гармония, мелодия и ритм, которые можно сравнить с числовыми операциями — сложением, умножением и делением. Также в музыке и математике существуют определенные законы, которые помогают создавать гармоничные и красивые композиции.

Ряды и последовательности, такие как геометрические прогрессии и ряды Фибоначчи, присутствуют как в математике, так и в музыке. Например, музыканты используют музыкальные ряды для создания гармоний, и эти ряды также имеют математическую основу.

Аналогии между музыкой и математикой расширяются и на более глубокий уровень. Некоторые известные композиторы, такие как Бах, были учеными и применяли математические принципы в своих музыкальных творениях.

Таким образом, связь между музыкой и математикой не только близка, но и важна для понимания основ и создания гармоничных композиций.

Гармония: математические законы и музыкальные принципы

Гармония является одним из важнейших музыкальных принципов, и она имеет глубокие связи с математическими законами. В основе гармонии лежит система тональностей, которая состоит из последовательности звуковых высот, и каждый звучащий тон относится к громкости и длительности.

Музыкальные инструменты производят звуки, которые состоят из гармонических колебаний, и эти колебания можно описать с помощью математических формул. Например, частота звука зависит от частоты колебаний инструмента, и это может быть выражено в герцах.

Часто гармония в музыке определяется с помощью интервалов, расстояний между звуками, и важным понятием является унисон — это совпадение высоты звуков. Также в гармонии используются такие интервалы, как кварта, квинта, септима и октава, которые определяются отношением частот звуков.

Очень важно, чтобы музыкальная гармония была воспринимаема слушателем и не вызывала диссонанса или несоответствия. В этом случае математические принципы и формулы могут помочь музыкантам создавать гармонию в своих композициях, основываясь на конкретных математических соотношениях.

Также гармония имеет важное значение в музыкальной теории, и она может быть изучена с помощью различных формул и алгоритмов. Музыканты и математики продолжают исследовать связь между гармонией и математическими законами, и такое исследование помогает расширять наше понимание музыки и математики в целом.

Вопрос-ответ:

Как связана математика с музыкой?

Математика и музыка тесно связаны друг с другом. Многие композиторы используют математические закономерности в своем творчестве, такие как гармония, ритм, мелодия. Например, законы гармонии и тоники могут быть выражены через математические функции.

Как математические принципы помогают в создании музыки?

Математические принципы помогают композиторам создавать более гармоничную и балансированную музыку. Некоторые композиторы используют золотое сечение, чтобы определить отношения во временных интервалах между нотами. Также можно использовать математические трюки, чтобы создать разнообразие и смену в ритме.

Как математика и музыка влияют на развитие личности?

Изучение математики и музыки способствует развитию личности, расширению кругозора и креативности. Математические трюки могут помочь создавать более сложную музыку, а знание принципов музыки может помочь в изучении и понимании математических закономерностей.

Можно ли использовать музыку и математику для лечения?

Да, музыка и математика могут использоваться для лечения различных заболеваний. Музыкальная терапия может помочь снизить уровень стресса и боли, а также помочь восстановлению после травм. Математические задания и игры могут помочь в расширении кругозора и уменьшении негативного воздействия стресса на организм.

Какие композиторы использовали математические принципы в своем творчестве?

Многие композиторы использовали математические принципы в своем творчестве. Например, Йоганн Себастьян Бах использовал математические принципы в своих фугах, а Моцарт использовал золотое сечение в своих сочинениях.

Как математика влияет на понимание музыки у слушателя?

Знание математических закономерностей может помочь научиться лучше понимать и наслаждаться музыкой. Например, знание принципов гармонии может помочь понять, почему некоторые аккорды звучат гармонично, а другие нет.

Какие исследования были проведены в области взаимодействия музыки и математики?

Было проведено множество исследований в области взаимодействия музыки и математики. Некоторые исследования показали, что изучение музыки может улучшить понимание и использование математических принципов, а другие исследования показали, что математические принципы могут помочь композиторам создавать более гармоничную музыку.

Ритм: связь музыки и математической теории

Ритм – одна из важнейших составляющих музыки. Это постоянное движение звуков, которое создает определенный паттерн и подчеркивает музыкальную структуру. Оказывается, связь между ритмом и математической теорией была замечена еще древними музыкантами.

Известно, что многие музыкальные жанры существуют благодаря регулярному размещению «сильных» и «слабых» ударов. Это можно интерпретировать как математическую последовательность, отражающую определенный закономерный порядок. Именно поэтому ритмическая теория, как и музыка в целом, вызывает интерес у математиков и научных исследователей музыкальных технологий.

Некоторые теоретики полагают, что даже сама природа обладает математической последовательностью и ритмичностью, которые можно услышать в звуках водопадов, пения птиц или шелесте листвы.

Сегодня многие композиторы используют различные математические методы и программы для создания интересных ритмических структур. Под действием электронных эффектов ритм становится еще более комплексным и зачастую беспредельным.

• В заключение, стоит сказать, что ритм и математическая теория — это два аспекта, которые оказывают огромное влияние на современную музыку и ее развитие.
• Будущее музыки заключается в объединении от магии искусства с виртуозностью математической теории.
• Гибрид ритма, музыкального мелодизма и математической формулы приводит к созданию потрясающей музыки, которую мы слушаем и наслаждаемся.

Сочетания звуков и логарифмическая шкала

В музыке каждый звук имеет свой тон и выражается в герцах (Гц). Однако, люди воспринимают звуки не линейно, а логарифмически. Это связано с тем, что наше ухо более чувствительно к изменениям низких частот, а высокие частоты воспринимаются менее чувствительно. Поэтому, чтобы оценить громкость звука, используется логарифмическая шкала децибел (dB).

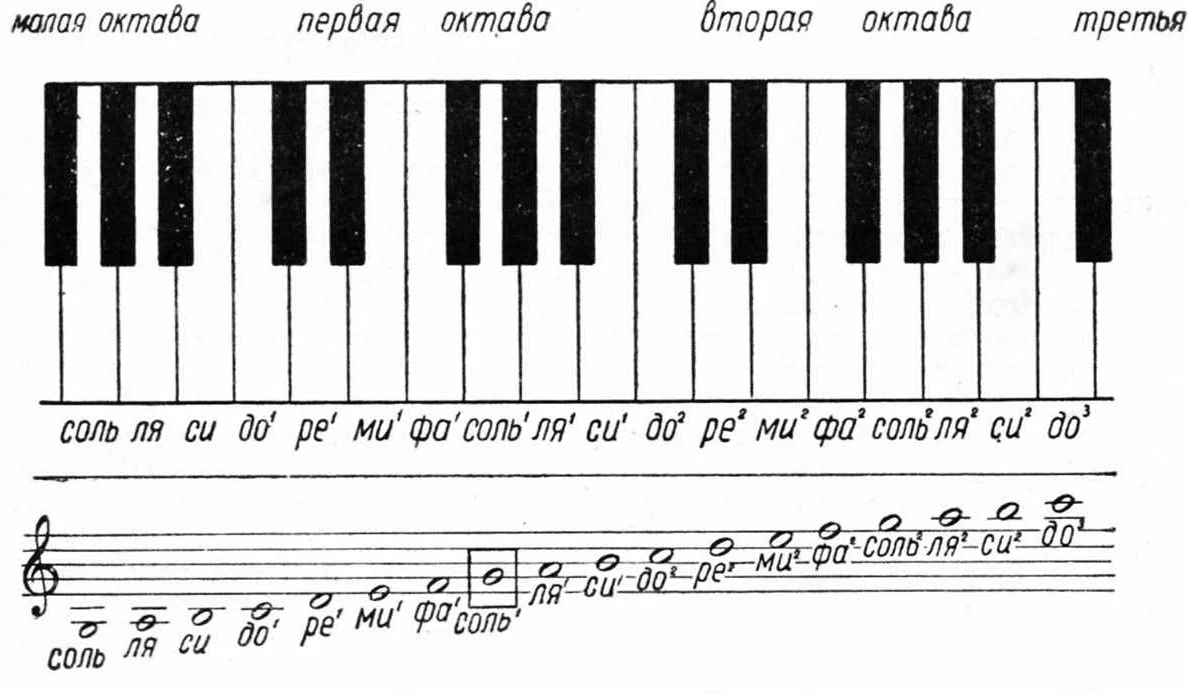
В музыке существуют сочетания звуков, которые звучат одновременно и создают гармонию. Их частоты взаимодействуют друг с другом и образуют целые числа, называемые гармоническими отношениями. Например, при сочетании двух нот: основной (главной) и ее октавной повторяющейся ноты, частота октавной должна быть в два раза больше, чем у главной.

Интересно, что логарифмическая шкала и гармонические отношения используются не только в музыке, но и в других областях. Например, в науке для измерения уровня звука или в инженерии для расчета акустических систем. Таким образом, математика и музыка связаны не только в звукоподражании, но и в применении одних и тех же законов и формул.

Размерность и темп: влияние математической точности

Музыка, как и математика, базируется на точности и логике. В музыке настраиваются инструменты, выбираются ноты, темп и размерность. Интересно, что размерность музыкальной композиции может быть представлена в математической форме.

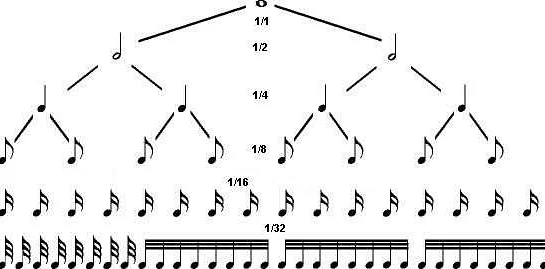
Размерность музыки определяется числом долей в каждом такте. Например, размерность 2/4 означает, что в такте две четвертные ноты. Темп музыки также имеет связь с математикой. Он определяет количество ударов в минуту, что также может быть выражено числом.

Математическая точность в размерности и темпе музыки необходима для того, чтобы композиция звучала гармонично. Не соответствующий размерности или темпу ритм может вызвать дискомфорт у слушателя. Интересно, что композиторы часто используют математические формулы для создания гармоничных музыкальных произведений.

• Например, Фибоначчиевы числа могут использоваться для определения длительности звуков и пауз в композиции.
• Также есть математические формулы, позволяющие определить идеальный темп исполнения для конкретной композиции.

Таким образом, математика и музыка тесно связаны друг с другом. Использование математической точности в размерности и темпе музыки не только позволяет создавать гармоничные произведения, но и дает возможность анализировать исторические и современные музыкальные тренды и взаимосвязи.

Арфа Пифагора и ёмкостные клавиши: исторические инновации

Арфа Пифагора была изобретена греческим философом и математиком Пифагором в V веке до нашей эры. Этот музыкальный инструмент был создан на основе законов и геометрических пропорций, которые были открыты самим Пифагором.

Ёмкостные клавиши — инновация, которая появилась в музыкальном инструментарии в XIX веке. Эта технология позволяет изменять тональность и звучание инструмента без необходимости перенастраивания струн. Принцип работы ёмкостных клавиш основан на использовании электрических свойств материалов — те, которые близки к клавишам, находятся в электрической взаимосвязи с нижними струнами.

Хотя эти два инновационных инструмента были созданы сотни лет разницы, они оба являются примерами того, как математика и физика могут быть использованы для улучшения музыкальных инструментов.

Также стоит отметить, что многие современные инструменты используют принципы математики и физики в своем дизайне и конструкции, что позволяет им быть более точными, тонкими и динамичными по звучанию.

Музыкальные инструменты, основанные на математических законах

Многие музыкальные инструменты имеют геометрические формы и физические свойства, которые могут быть описаны исключительно математически. Например, длина струны гитары, флейты или скрипки является основой определения высоты звука, который она издает. Всякий раз, когда играете на гитаре, чтобы получить определенный звук, необходимо изменять длину струны или ее толщину.

Кроме того, математика может использоваться для создания новых инструментов, основанных на новых физических принципах. Например, Эрик Бойер, американский компьютерный ученый и музыкант, создал новый инструмент, называемый «fractal guitar» на основе принципов фрактальной геометрии. Он использует множественные генераторы звуковых волн для создания бесконечных и разнообразных мелодий и звуков.

Также математические законы применяются при проектировании ударных инструментов, таких как барабаны. Улучшение процесса создания и совершенствования ударных инструментов может быть сделано, исходя из знаний физических свойств звука и экспериментальных данных, полученных во время игры.

Таким образом, понимание математических законов играет важную роль в развитии музыкальных инструментов и обеспечивает большую свободу в творческом процессе создания музыки.

Цифровая звукозапись и математическая обработка аудио сигналов

Математика играет огромную роль в цифровой звукозаписи. Каждый музыкальный трек, который мы слушаем сегодня, начинается с записи звука в формате цифрового сигнала. Цифровые сигналы представляют собой бинарные данные, которые могут быть обработаны на компьютерах и других цифровых устройствах. Для того, чтобы записать звук в цифровом формате, используется процесс, называемый аналого-цифровым преобразованием, которое основано на математических принципах.

Звуковой сигнал человеческого голоса или музыкального инструмента представляет собой колебания звуковых волн в воздухе. Одним из основных параметров звуковых волн является частота, которая определяет тон звука. Для того, чтобы записать звук в цифровом формате, необходимо дискретизировать сигнал по времени и по амплитуде. Это означает, что звук воспринимается компьютером как последовательность чисел.

Цифровые сигналы могут быть обработаны с помощью математических алгоритмов, которые могут изменять тембр, громкость и другие параметры звука. Один из примеров математической обработки аудио сигналов — это эффект «эхо», который создается путем наложения звука на себя с задержкой и изменением амплитуды. Другим примером является использование преобразования Фурье для анализа спектра звука и создания эквалайзера для изменения тембра звука.

Таким образом, цифровая звукозапись и математическая обработка аудио сигналов тесно связаны друг с другом и играют важную роль в создании современной музыки. Благодаря развитию технологий и математическим новшествам, мы можем наслаждаться новыми звуковыми эффектами и переживать эмоции от прекрасной музыки в привычной нам цифровой форме.

Музыка как способ развития математического мышления у детей

Музыка является полезным и интересным способом развития математического мышления у детей разного возраста. Ритм, мелодия и гармония в музыке требуют использования математических принципов и концепций, которые могут быть абстрактными и трудными для понимания, но благодаря музыке они становятся более доступными и понятными для детей.

Особенно важно заметить, что дети, которые учатся играть на музыкальных инструментах, имеют преимущество в развитии математической мышления. Это связано с тем, что при игре на инструменте дети учатся разбираться в музыкальных нотах, времени, темпе, а также учатся рассчитывать интервалы и подсчитывать ноты в композициях. Все эти навыки требуют высокой математической подготовки и способствуют развитию абстрактного мышления.

Программы дополнительного образования по музыке могут стать полезным инструментом для детей, желающих улучшить свои навыки в математике. Игры, песни и другие методы обучения музыке помогут укрепить навыки математического мышления, а также дадут детям возможность общаться со сверстниками и развивать социальные навыки.

Итак, музыка является эффективным способом развития математического мышления у детей. Она помогает детям овладеть абстрактным мышлением, необходимым для понимания математических концепций, а также способствует развитию социальных и коммуникативных умений. Родители и учителя могут использовать музыку в качестве невероятного инструмента для развития полезных навыков у детей.

Математика и музыка в современных исследованиях: перспективы

Современные исследования в области математики и музыки демонстрируют неизменную взаимосвязь этих двух дисциплин. По мере того, как мы продвигаемся в науке и технологиях, все больше возможностей открываются для изучения музыки через математику.

Ключевые области современных исследований включают математический анализ музыкальных форм, приложения теории чисел к музыке и математические модели звука.

Перспективы в этом направлении исследований также включают разработку новых инструментов для анализа и синтеза музыки, использующих математические алгоритмы и модели. Это может быть полезно не только для создания новой музыки, но и для решения практических задач, например, в области звукозаписи и звуковой обработки.

Таким образом, математика и музыка продолжают играть важную роль в различных областях научных исследований. Изучение этих дисциплин взаимосвязано и дополняет друг друга, предоставляя новые возможности для развития и применения знаний в различных областях науки и технологий.