Математические распределения с высоким математическим ожиданием: где их искать и как работать с ними

Статья о распределениях с математическим ожиданием больше 1, в которой разбираются различные виды таких распределений и их особенности. Узнайте, как эти распределения влияют на статистический анализ данных и как их можно использовать в реальной жизни.

Распределения с математическим ожиданием больше 1 являются важным объектом изучения вероятностного анализа. Они встречаются в различных областях математики, физики, экономики и других наук. Рассмотрение таких распределений позволяет получать важные выводы о случайных явлениях.

В данной статье мы рассмотрим несколько примеров распределений с математическим ожиданием больше 1, таких как нормальное, Пуассона, биномиальное, геометрическое и другие. Мы также обсудим особенности этих распределений, их графики, формулы и применения в реальных задачах.

Изучение распределений с математическим ожиданием больше 1 позволяет лучше понять случайные явления и предсказывать их поведение в будущем. Вся информация, представленная в данной статье, поможет читателю расширить свои знания и применять их на практике.

Примеры распределений с математическим ожиданием больше 1

Распределения с математическим ожиданием (средним значением) больше 1 широко используются в различных областях, включая экономику, физику, биологию и т.д. Ниже приведены несколько примеров распределений, где математическое ожидание больше 1.

• Геометрическое распределение. Это распределение описывает вероятность того, что первый успех произойдет в определенный момент времени. Например, если мы бросаем монету до тех пор, пока не выпадет орел (т.е. получим первый успех), то количество бросков до этого момента имеет геометрическое распределение. Математическое ожидание геометрического распределения равно 1/p, где p — вероятность успеха (например, вероятность выпадения орла).
• Распределение Пуассона. Это распределение описывает вероятность того, что определенное число событий произойдет за определенный промежуток времени. Например, количество посетителей сайта в определенный день может иметь распределение Пуассона. Математическое ожидание распределения Пуассона равно λ, где λ — среднее количество событий за интервал времени.
• Распределение Лапласа. Это распределение описывает разность между двумя случайными величинами, которые имеют одинаковое распределение. Распределение Лапласа также может использоваться для моделирования случайных шумов в сигналах или измерениях. Математическое ожидание распределения Лапласа равно 0, а среднее абсолютное отклонение равно 1/λ, где λ — параметр масштаба распределения.

Выше приведены только несколько примеров распределений с математическим ожиданием больше 1. Важно помнить, что для каждого конкретного случая необходимо выбирать соответствующее распределение, учитывая особенности задачи и доступные данные.

Видео по теме:

Особенности распределений с математическим ожиданием больше 1

Распределения, где математическое ожидание больше 1, имеют свои особенности и характеристики. Они отличаются от распределений с меньшим математическим ожиданием и могут быть использованы для анализа различных явлений.

В отличие от распределений с меньшим математическим ожиданием, распределения с ожиданием больше 1 имеют длинный хвост справа. Это означает, что вероятность появления значений, которые находятся далеко от среднего, выше, чем в распределениях с ожиданием меньше 1. Данные распределения могут быть использованы для моделирования явлений, таких как распределение доходов или цен на недвижимость.

Ещё одной особенностью распределений с математическим ожиданием больше 1 является то, что их дисперсия также выше, чем у распределений с меньшим математическим ожиданием. Это означает большую разницу между значениями и средним значением в распределении. Большая дисперсия может быть использована для моделирования аномалий в данных или экстремальных событий.

Еще одной важной особенностью данных распределений является то, что их среднее значение может быть склонно к смещению на определенные значения. Это может быть связано с смещением в данных, которое может быть вызвано определенными факторами, такими как преобладание определенных значений в выборке.

В целом, распределения с математическим ожиданием больше 1 имеют свои уникальные особенности и могут быть использованы для моделирования различных явлений, связанных с поведением данных в экстремальных случаях.

Нормальное распределение с математическим ожиданием больше 1

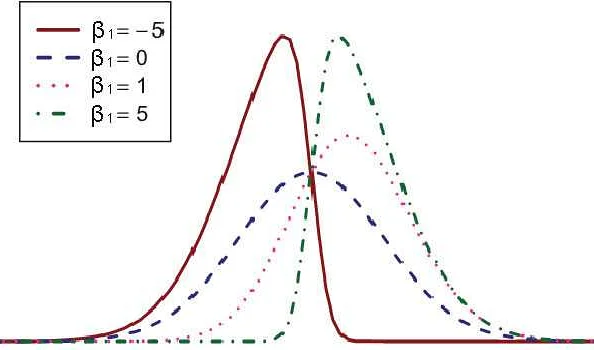
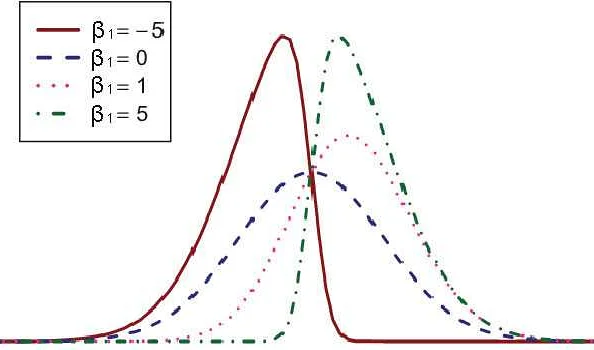
Нормальное распределение, также известное как распределение Гаусса, является одним из наиболее распространенных распределений в статистике. Это распределение имеет симметричную колоколообразную форму, которая характеризуется двумя параметрами: математическим ожиданием и стандартным отклонением.

Если математическое ожидание нормального распределения больше 1, то это означает, что среднее значение выборки, которая взята из этого распределения, будет больше 1. Чем больше будет математическое ожидание, тем больше будет смещена вправо колоколообразная форма распределения.

Нормальное распределение с математическим ожиданием больше 1 может быть полезным при анализе данных, связанных с производственными процессами, где большие значения являются более интересными для изучения, чем маленькие значения. Например, если мы рассматриваем распределение доходов населения, то мы можем ожидать, что средний доход будет больше 1, что подтверждается экономической теорией.

Характеристики нормального распределения с математическим ожиданием больше 1 могут быть рассчитаны с помощью соответствующих формул, которые используются в статистическом анализе данных. Также можно использовать программное обеспечение для статистического анализа данных для генерации распределения и расчета соответствующих характеристик.

Вопрос-ответ:

Что такое математическое ожидание распределения?

Математическое ожидание — это среднее значение случайной величины в распределении. Оно определяется как сумма произведений значений случайной величины на их вероятности в данном распределении. В простых случаях можно вычислить математическое ожидание аналитически, но в более сложных случаях приходится использовать численные методы.

Как определить, что математическое ожидание распределения больше 1?

Для того, чтобы определить, что математическое ожидание распределения больше 1, нужно вычислить его аналитически или численно, а затем сравнить с единицей. Если значение больше единицы, то математическое ожидание распределения больше 1.

Каковы примеры распределений с математическим ожиданием больше 1?

Примерами распределений с математическим ожиданием больше 1 являются, например, гамма-распределение, экспоненциальное распределение, Парето-распределение и т.д. Эти распределения широко используются в статистических исследованиях и моделировании случайных процессов.

Насколько точными должны быть значения, чтобы можно было утверждать, что математическое ожидание распределения больше 1?

Точность значений зависит от конкретных условий задачи и выбранного метода вычисления математического ожидания. В любом случае, если значение математического ожидания явно больше единицы или имеет статистическую значимость, то можно утверждать, что распределение имеет математическое ожидание больше 1.

Какие основные особенности у распределений с математическим ожиданием больше 1?

Основной особенностью распределений с математическим ожиданием больше 1 является то, что они характеризуются более высокими значениями случайной величины, чем распределения с математическим ожиданием меньше 1. Это означает, что существует большая вероятность того, что значение случайной величины будет более высоким, чем при других распределениях. Кроме того, такие распределения имеют более тяжелые «хвосты», что может приводить к неожиданным результатам в некоторых приложениях.

Какие методы используются для вычисления математического ожидания распределения?

Для распределений, имеющих аналитические функции распределения, можно вычислить математическое ожидание аналитически. Если аналитическое решение невозможно, используют численные методы, такие как метод Монте-Карло или метод Марковских цепей. В более сложных случаях требуются приближенные методы, такие как методы аппроксимации или симуляции.

Какие приложения имеют распределения с математическим ожиданием больше 1?

Распределения с математическим ожиданием больше 1 широко используются в приложениях, связанных с измерением рисков, таких как финансовые аналитические приложения, а также в исследованиях в области медицины, экономики и науки о климате. Они также используются в моделировании случайных процессов и в качестве моделей для различных типов данных.

Распределение Пуассона с математическим ожиданием больше 1

Распределение Пуассона – это дискретное распределение вероятностей, которое описывает количество событий, происходящих за фиксированный промежуток времени или в фиксированном объеме. Распределение Пуассона имеет один параметр λ (лямбда), который является математическим ожиданием и дисперсией распределения.

Если λ больше 1, то это означает, что среднее количество событий больше одного за фиксированный период времени. Например, распределение Пуассона может использоваться для моделирования количества аварий на дорогах за день или количества клиентов, посещающих магазин в час.

В распределении Пуассона с λ больше 1 вероятность нахождения значений близких к нулю снижается, а вероятность нахождения значений больших чем λ, увеличивается. Это означает, что в таком распределении больше вероятность получения значений, близких к среднему, и меньше вероятность получения значений, далеких от среднего значения.

Как и в случае с другими распределениями, при использовании распределения Пуассона необходимо учитывать особенности конкретной задачи, чтобы правильно выбрать параметр λ. Например, при моделировании клиентов, посещающих магазин, необходимо учитывать время работы магазина и возможность комбинирования приходов и уходов клиентов.

Геометрическое распределение с математическим ожиданием больше 1

Геометрическое распределение — это дискретное вероятностное распределение, которое моделирует время до первого наступления события в процессе Бернулли. Распределение определяется вероятностью успеха и неудачи в каждом испытании.

В случае, если вероятность успеха больше 0,5, математическое ожидание геометрического распределения будет больше 1. Это связано с тем, что в таком случае вероятность успеха в испытании больше вероятности неудачи, соответственно, время до первого успеха будет в среднем больше 1.

Примером может быть моделирование времени до поиска необходимой информации на интернет-странице. Если вероятность успешного поиска информации выше 0,5, то среднее время до ее нахождения будет больше 1.

Геометрическое распределение с математическим ожиданием больше 1 имеет свои особенности, среди которых можно выделить тот факт, что оно не является асимметричным, и также не обладает свойством «отрицательной биномиальной» распределенности, когда требуется определенное число успешных исходов в процессе Бернулли.

Отрицательное биномиальное распределение с математическим ожиданием больше 1

Отрицательное биномиальное распределение – это дискретное распределение вероятностей, которое описывает количество испытаний, необходимых для получения определенного числа успехов. В отличие от биномиального распределения, где мы фиксируем количество испытаний и ищем вероятность определенного числа успехов, в отрицательном биномиальном распределении мы фиксируем количество успехов и ищем вероятность, что потребуется определенное количество испытаний для их получения.

Для определения отрицательного биномиального распределения нам потребуется два параметра: количество успехов и вероятность успеха в каждом испытании. Математическое ожидание отрицательного биномиального распределения равно (1- p)/p, где p — вероятность успеха.

Если математическое ожидание отрицательного биномиального распределения больше 1, то это говорит о том, что среди необходимых для получения определенного числа успехов испытаний мы ожидаем получить более одного успеха. Такие распределения могут применяться для моделирования процессов, где вероятность успеха не меняется от испытания к испытанию и где имеется большой набор потенциальных исходов.

Например, отрицательное биномиальное распределение с математическим ожиданием больше 1 может быть использовано для моделирования количества вызовов к экстренной службе пожарной охраны в течение ночи, где вероятность вызова находится на стабильном уровне и каждый вызов независим от предыдущего. С помощью такого распределения мы можем оценить, сколько вызовов мы можем ожидать в среднем за ночь и какова вероятность, что нам потребуется дополнительный вызов.

Гипергеометрическое распределение с математическим ожиданием больше 1

Гипергеометрическое распределение – это дискретное распределение вероятностей, в котором мы выбираем элементы из конечной группы без замены и описываем вероятность выбора определенного количества элементов из определенной группы. Одной из особенностей гипергеометрического распределения является возможность получить математическое ожидание, которое больше единицы.

Математическое ожидание гипергеометрического распределения можно выразить формулой:

E(X) = n * K / N,

где n – общее количество элементов, K – количество нужных нам элементов, а N – количество элементов, из которых мы выбираем.

Таким образом, если количество нужных нам элементов K более чем половина от общего количества элементов, то математическое ожидание будет больше единицы.

Примером применения гипергеометрического распределения с математическим ожиданием больше 1 может служить изучение социально-демографических групп в определенной стране.

К примеру, если мы хотим определить вероятность того, что в группе людей, имеющих высшее образование, будет больше женщин, чем мужчин, то мы можем использовать гипергеометрическое распределение. Если количество людей, имеющих высшее образование, больше чем количество мужчин в этой группе, то математическое ожидание будет больше единицы.

Равномерное распределение с математическим ожиданием больше 1

Равномерное распределение является одним из наиболее простых видов вероятностных распределений, которое описывает ситуацию, когда все значения вероятности равны между собой. В случае, когда математическое ожидание больше 1, это означает, что присутствуют значения, которые встречаются с большей вероятностью.

Например, если имеется распределение от 1 до 10, то в случае, когда математическое ожидание равно 5.5, значения 6, 7, 8 и 9 будут встречаться чаще, чем значения 1, 2, 3, 4 и 10.

Такое распределение может иметь множество применений в реальных задачах, таких как финансовые рынки, исследование социальных процессов и т.д.

Стоит отметить, что равномерное распределение с математическим ожиданием больше 1 может быть смещенным в правую сторону, что означает наличие более высоких значений на правом конце диапазона. Например, если распределение описывает доходы людей, то наличие большого количества людей с высокими доходами может привести к такому смещению вправо.

Суммируя, равномерное распределение с математическим ожиданием больше 1 — это распределение, в котором значения с более высокой вероятностью встречаются на более высоких уровнях. Оно может иметь множество применений в реальной жизни и может быть смещенным вправо в случае наличия более высоких значений на правом конце диапазона.

Логнормальное распределение с математическим ожиданием больше 1

Логнормальное распределение – это распределение вероятностей, в котором логарифмы случайных величин имеют нормальное распределение. Одной из основных особенностей этого распределения является то, что оно может быть использовано для моделирования данных, которые имеют только положительные значения, а также для данных, которые подчиняются экспоненциальному закону.

Как правило, логнормальное распределение применяется для моделирования ряда финансовых данных, таких как цены акций, доходности инвестиций и других финансовых показателей. Несмотря на это, оно также может использоваться для моделирования разнообразных процессов и явлений в экологии, биологии, геологии, медицине и других областях.

Когда математическое ожидание логнормального распределения больше 1, это означает, что распределение имеет смещение вправо. То есть, большая часть значений случайной величины находится на больших значениях и меньшая часть – на меньших. Этот факт может быть использован в практике при принятии решений о финансовых инвестициях или других аналогичных задачах, где важны высокие значения показателей.

Важно отметить, что логнормальное распределение является сложным для анализа математическими методами и может потребовать применения численных методов в вычислениях. Также, при использовании данного распределения необходимо учитывать, что оно не является универсальным и может не подходить для моделирования некоторых видов данных.

Экспоненциальное распределение с математическим ожиданием больше 1

Экспоненциальное распределение является одним из наиболее важных распределений в статистике. Оно широко используется для анализа различных моделей, например, для моделирования времени между событиями. Однако, в различных ситуациях может быть нужно распределение с более высоким математическим ожиданием. Существуют экспоненциальные распределения с математическим ожиданием, превышающим 1.

Экспоненциальное распределение с математическим ожиданием равным 1 обычно используется для моделирования времени между последовательными событиями, где время между событиями является случайной величиной. Однако, во многих случаях время между событиями может быть больше единицы. В таких случаях использование экспоненциального распределения с математическим ожиданием больше 1 может быть эффективнее.

Важной особенностью экспоненциального распределения с математическим ожиданием больше 1 является то, что оно является распределением с памятью, то есть вероятностная функция распределения определяется не только текущим значениями случайной величины, но и предыдущими значениями. Также важно понимать, что с увеличением математического ожидания распределения, уменьшается дисперсия, что может сказаться на точности модели.

В целом, экспоненциальное распределение с математическим ожиданием больше 1 может быть полезным при моделировании многих процессов и является хорошим инструментом для анализа данных с высокими математическими ожиданиями.

Распределение Бернулли с математическим ожиданием больше 1

Распределение Бернулли — это дискретное вероятностное распределение, которое описывает случайный эксперимент с двумя возможными исходами: успехом (вероятностью p) и неудачей (вероятностью 1-p).

Если математическое ожидание (среднее значение) распределения Бернулли больше 1, то это означает, что вероятность успеха превышает вероятность неудачи и наблюдения скорее всего будут позитивными. Например, если вероятность успеха равна 0,7, то среднее значение распределения Бернулли будет равно 0,7, что означает, что мы можем ожидать, что бóльшая часть экспериментов будут успешными.

Распределение Бернулли с математическим ожиданием больше 1 может быть использовано для моделирования сценариев, в которых очень вероятно достижение желаемого результата. Например, это может быть использовано для прогнозирования вероятности победы в казино или вероятности успеха продаж на рынке.

Однако, следует отметить, что распределение Бернулли не может быть использовано для моделирования событий, которые не являются независимыми. Также, распределение Бернулли может дать нереалистичные результаты в случаях, когда вероятность успеха очень близка к 1 или к 0.