Математика 6 класс дорофеев что такое отношение
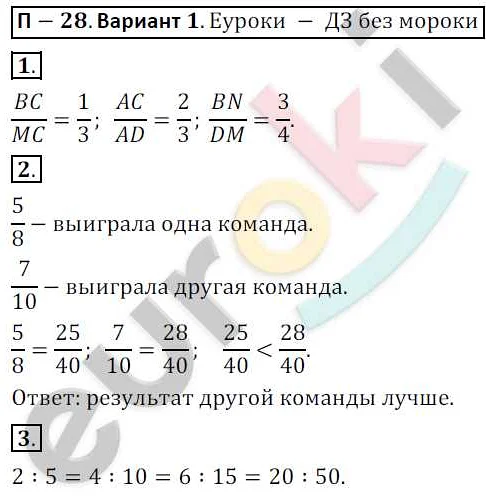
Содержимое
- 1 Математика 6 класс дорофеев что такое отношение
- 1.1 Что такое отношение в математике 6 класса Дорофеев
- 1.2 Понятие отношения в математике
- 1.3 Примеры отношений в повседневной жизни
- 1.4 Как определить отношение в математике
- 1.5 Методы представления отношений
- 1.6 Графическое представление отношений
- 1.7 Способы определения отношений на множествах
- 1.8 Вопрос-ответ:
- 1.9 Символическое представление отношений
- 1.10 Видео по теме:
Отношение в математике 6 класса по учебнику Дорофеева — это способ сравнения двух или более чисел или объектов. Ученики изучают понятие отношения, его свойства и применение в задачах на конкретных примерах. В данной статье рассматривается содержание урока по отношениям в 6 классе по учебнику Дорофеева и приводятся примеры задач для закрепления материала.
В математике отношение — это особый вид связи между элементами двух множеств. Оно позволяет определить, какие из этих элементов находятся в определенной связи друг с другом. Знание и понимание отношений является важным элементом в изучении математики и помогает решать различные задачи и задания.
Определение отношения может быть представлено различными способами. Одним из них является таблица, в которой указываются элементы первого и второго множеств, а также их связь. Другим способом является графическое представление отношения в виде стрелок, соединяющих элементы двух множеств.
Отношения могут быть различных типов: функциональные, эквивалентные, порядковые и т.д. Функциональные отношения характеризуются тем, что каждому элементу первого множества соответствует только один элемент второго множества. Эквивалентные отношения обладают свойством симметричности и рефлексивности. Порядковые отношения позволяют упорядочить элементы двух множеств по определенным правилам.
Изучение отношений в математике позволяет развить абстрактное мышление и логику, а также научиться анализировать и решать различные задачи. Математика 6 класс Дорофеев содержит подробное объяснение теории отношений и множеств, а также предлагает много практических заданий и упражнений для закрепления полученных знаний.
Что такое отношение в математике 6 класса Дорофеев

Отношение может быть представлено в виде упорядоченной пары чисел или элементов. Например, отношение «больше» между числами 5 и 3 можно записать как (5, 3), где первое число больше второго.
В математике 6 класса Дорофеев отношение широко используется для анализа различных задач. Оно помогает устанавливать связи между числами, объектами или явлениями и решать различные задачи с использованием этих связей.
Отношение может быть задано графически с помощью диаграммы Эйлера или таблицы. В диаграмме Эйлера элементы множеств изображаются в виде кругов, а связи между ними — пересечениями кругов. В таблице отношение представляется в виде матрицы, в которой элементы множества располагаются в строках и столбцах, а связи указываются в соответствующих ячейках.
Важно понимать, что отношение может быть разным и зависит от контекста задачи. Например, в одной задаче отношение может описывать равенство двух чисел, а в другой задаче — отношение «больше». Поэтому важно внимательно читать условие задачи и правильно определить отношение, которое необходимо использовать для ее решения.
Понятие отношения в математике
Отношение может быть задано с помощью таблицы, графика, формулы или словесного описания. Например, отношение «больше» может быть задано таблицей, где каждое число из первого множества связано с числом из второго множества, которое больше его.
Отношение может быть обозначено различными символами, например: «=», «», «≥», «≤». Использование этих символов позволяет определить, какие элементы связаны между собой и в каком порядке.
Отношение может иметь различные свойства, такие как рефлексивность, симметричность и транзитивность. Рефлексивное отношение означает, что каждый элемент первого множества связан с самим собой. Симметричное отношение означает, что если элемент A связан с элементом B, то элемент B также связан с элементом A. Транзитивное отношение означает, что если элемент A связан с элементом B, и элемент B связан с элементом C, то элемент A также связан с элементом C.
Изучение отношений в математике позволяет анализировать различные связи между элементами множеств и решать разнообразные задачи. Отношения могут быть применены в различных областях, таких как физика, экономика, информатика и другие.
Примеры отношений в повседневной жизни
Отношение расстояния к времени: В повседневной жизни мы часто измеряем расстояние и время, чтобы определить скорость движения. Например, при езде на автомобиле мы можем измерить расстояние в километрах и время в минутах, чтобы определить среднюю скорость движения.
Отношение цены к количеству товара: При покупке товаров мы часто сравниваем их цену и количество. Например, при выборе между двумя упаковками молока, мы можем сравнить их цену и количество молока в каждой упаковке, чтобы определить, какая упаковка предлагает лучшее соотношение цены и количества.
Отношение количества мужчин к женщинам: В обществе часто обсуждаются отношения между мужчинами и женщинами. Например, можно рассмотреть отношение количества мужчин к женщинам на рабочих местах, в политике или в образовании. Эти отношения могут быть предметом дискуссий и исследований.
Отношение успеха к усилиям: В жизни мы часто сталкиваемся с отношением между успехом и усилиями, которые мы прилагаем для достижения цели. Например, чтобы достичь успеха в учебе или спорте, необходимо приложить определенные усилия и потратить время на обучение или тренировки.
Отношение цены к качеству: При покупке товаров или услуг мы часто сравниваем их цену и качество. Например, при выборе между двумя смартфонами мы можем сравнить их цену и функциональные возможности, чтобы определить, какой смартфон предлагает лучшее соотношение цены и качества.
Отношение затрат к доходам: В финансовой сфере мы часто анализируем отношение между затратами и доходами. Например, при составлении бюджета семьи мы можем сравнить ежемесячные затраты и доходы, чтобы определить, в каких областях необходимо сократить расходы или увеличить доходы.
Как определить отношение в математике
Для определения отношения между двумя наборами объектов необходимо выполнить следующие шаги:
- Определить первый набор объектов, называемый исходным множеством, и обозначить его символом A.
- Определить второй набор объектов, называемый целевым множеством, и обозначить его символом B.
- Установить правило, по которому каждому элементу из множества A будет соответствовать элемент из множества B.
- Записать отношение в виде пар чисел, графа или таблицы в зависимости от поставленной задачи.
Например, пусть имеется множество A = {1, 2, 3} и множество B = {4, 5, 6}. Если установить правило, что каждому элементу из множества A будет соответствовать элемент из множества B, представим это отношение в виде таблицы:
AB
| 1 | 4 |
| 2 | 5 |
| 3 | 6 |
Таким образом, отношение между множествами A и B можно определить как {(1, 4), (2, 5), (3, 6)}.
Отношение в математике имеет широкое применение и используется для анализа и описания различных взаимосвязей. С помощью отношений можно решать задачи, моделировать процессы и строить логические цепочки.
Методы представления отношений

Один из методов представления отношений – это таблицы. В таблице каждый элемент отношения записывается в отдельной ячейке. Пересечение строки и столбца показывает, что между этими элементами существует связь. Таблицы удобно использовать для представления отношений с большим количеством элементов.
Другим методом представления отношений является граф. Граф представляет собой совокупность вершин и ребер, где вершины обозначают элементы отношения, а ребра – связи между этими элементами. Графы помогают наглядно показать структуру отношений, а также выявить различные свойства и закономерности.
Еще одним методом представления отношений является диаграмма Венна. Диаграмма Венна состоит из нескольких пересекающихся окружностей, каждая из которых представляет группу элементов отношения. Пересечение окружностей показывает, что между группами элементов существует связь. Диаграммы Венна часто используются для построения логических связей и определения пересечений и различий между различными группами элементов.
Каждый из этих методов представления отношений имеет свои преимущества и недостатки. Выбор конкретного метода зависит от целей и задач, которые требуется решить при анализе отношений.
Графическое представление отношений
Отношение между двумя множествами можно представить графически с помощью диаграмм Эйлера или диаграмм Венна. Эти диаграммы позволяют наглядно показать, какие элементы общие или различные для двух множеств.
Диаграмма Эйлера состоит из окружностей, представляющих каждое множество, и пересечения этих окружностей, которое показывает общие элементы. Если элемент принадлежит только одному множеству, он будет находиться внутри соответствующей окружности. Если элемент принадлежит обоим множествам, он будет находиться в пересечении окружностей.
Диаграмма Венна также использует окружности для представления множеств. Однако в этом случае элементы, принадлежащие только одному множеству, располагаются внутри соответствующей окружности. Общие элементы располагаются в пересечении окружностей.
Графическое представление отношений позволяет легче понять связь между множествами и увидеть, какие элементы являются общими или уникальными для каждого множества.
Способы определения отношений на множествах

Отношение между элементами двух множеств можно определить различными способами. В математике существует несколько основных методов определения отношений:
1. Перечисление элементов: отношение задается путем перечисления всех пар элементов, которые находятся в этом отношении. Например, для множества A = {1, 2, 3} и множества B = {a, b, c}, отношение R можно задать следующим образом: R = {(1, a), (2, b), (3, c)}.
2. Разрешение задачи: отношение может быть определено на основе решения конкретной задачи или условия. Например, задача может состоять в определении, является ли одно число делителем другого. В этом случае отношение может быть определено как множество всех пар чисел, где первое число является делителем второго числа.
3. Формула или правило: отношение может быть определено с использованием формулы или правила. Например, для отношения «больше» между элементами двух множеств можно использовать такую формулу: R = {(x, y) | x > y}.
4. Графическое представление: отношение может быть представлено в виде графа, где элементы множества являются вершинами, а отношение между элементами — ребрами. Например, если отношение задано как R = {(1, 2), (2, 3), (3, 1)}, то графическое представление будет выглядеть следующим образом:
1 —> 2
↑ |
| ↓
3 <—
Это основные способы определения отношений на множествах. В зависимости от контекста и задачи, один из этих способов может быть предпочтительным.
Вопрос-ответ:
Что такое отношение в математике?
Отношение в математике — это связь или соответствие между двумя множествами. Оно показывает, какие элементы первого множества связаны с элементами второго множества.
Как можно определить отношение?
Отношение можно определить, составив таблицу или график, в котором будут указаны все соответствующие элементы двух множеств. Если элементы первого множества связаны с элементами второго множества, то в таблице или графике будет указано соответствующее соединение или значение.
Какие бывают виды отношений?
В математике существуют различные виды отношений, такие как функциональное отношение, эквивалентность, порядок и другие. Каждый вид отношений имеет свои особенности и свойства, которые исследуются в соответствующих разделах математики.
Какие свойства имеют отношения?
Отношения могут быть рефлексивными, симметричными, транзитивными и антисимметричными. Рефлексивное отношение означает, что каждый элемент множества связан с самим собой. Симметричное отношение показывает, что если элемент A связан с элементом B, то элемент B также связан с элементом A. Транзитивное отношение означает, что если элемент A связан с элементом B, а элемент B связан с элементом C, то элемент A также связан с элементом C. Антисимметричное отношение означает, что если элемент A связан с элементом B и элемент B связан с элементом A, то A и B — один и тот же элемент.
Символическое представление отношений

Отношение между двумя множествами A и B можно представить с помощью символического обозначения. Это позволяет наглядно и кратко описать связь между элементами этих множеств.
Самым общим символическим обозначением отношения является стрелка, которая указывает на связанные элементы. Если элемент a из множества A связан с элементом b из множества B, то используется запись a → b. Если отношение является взаимным, то используется символ ↔, который указывает на двустороннюю связь между элементами.
Если отношение между элементами является частичным порядком, то используются знаки ≤ или ≥, которые указывают на то, что один элемент меньше или больше другого.
Также для отношений могут использоваться символические обозначения, которые описывают другие свойства отношений, например, «принадлежит», «не принадлежит», «является подмножеством», «не является подмножеством».
Символическое представление отношений очень удобно при работе с математическими задачами, так как позволяет кратко и точно описать связь между элементами множества.




