Что такое диаграмма множеств в математике

Диаграмма множеств в математике — это графическое представление отношений и связей между различными множествами. Узнайте, какие типы диаграмм используются, как они строятся и как они помогают визуализировать сложные концепции и отношения в математике.

В математике диаграмма множеств — это графическое представление отношений между различными множествами. Она помогает визуализировать и анализировать связи между элементами и подмножествами. Диаграммы множеств часто используются в математическом анализе, логике, теории множеств и информатике.

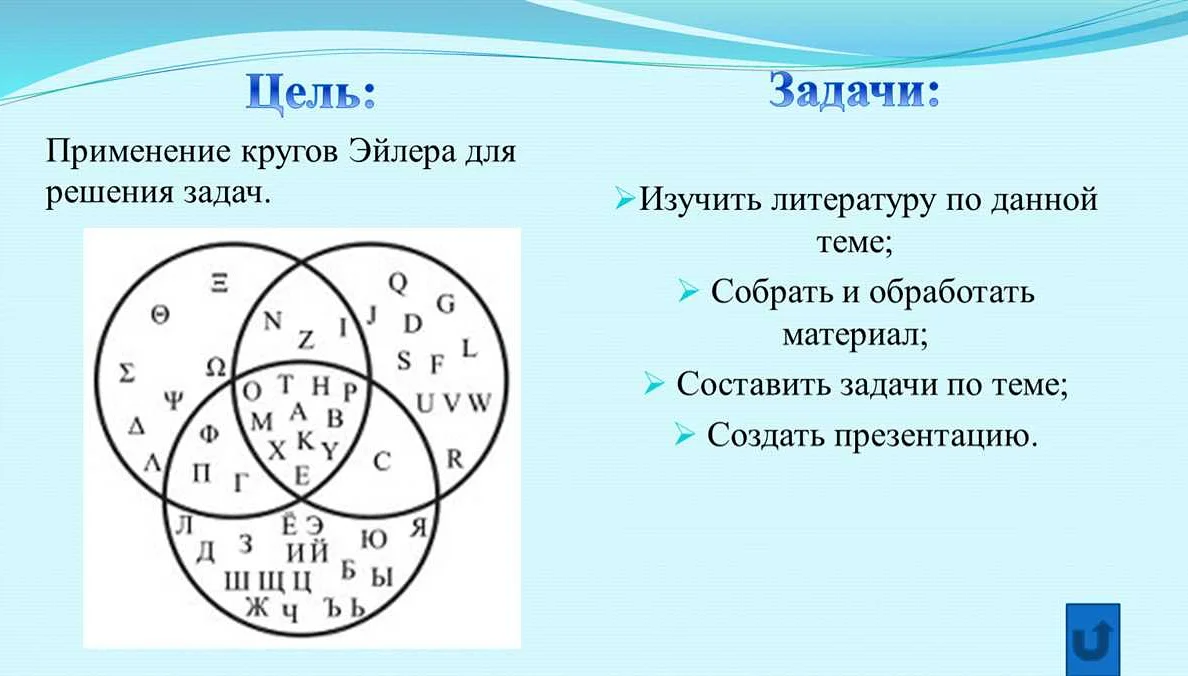
Одной из самых распространенных форм диаграмм множеств является диаграмма Эйлера-Венна. Она состоит из пересекающихся окружностей или эллипсов, каждый из которых представляет множество. Области пересечения представляют собой совместные элементы двух или более множеств.

Например, предположим, что есть два множества: «A» — множество всех четных чисел от 1 до 10, и «B» — множество всех чисел, кратных 3 от 1 до 10. Диаграмма множеств для этих двух множеств будет состоять из двух пересекающихся окружностей. Область пересечения будет представлять собой множество чисел, которые одновременно являются четными и кратными 3, то есть {6}.

Диаграммы множеств широко применяются в различных областях. Например, они используются для анализа логических отношений, моделирования данных, классификации объектов и демонстрации результатов исследований. Они также являются полезным инструментом в учебе и позволяют визуально представлять абстрактные концепции и связи между ними.

Что такое диаграмма множеств в математике?

Диаграммы множеств состоят из кругов или прямоугольников, представляющих множества, и линий или стрелок, обозначающих связи или отношения между ними. Они могут быть простыми или сложными в зависимости от количества и сложности отношений, которые нужно представить.

Диаграммы множеств являются полезным инструментом для анализа данных и решения задач в различных областях, таких как логика, теория множеств, теория графов, теория вероятностей и др. Они помогают наглядно представить структуру данных и выявить взаимосвязи между элементами.

Для создания диаграмм множеств можно использовать различные методы и средства визуализации, такие как круговая диаграмма, диаграмма Венна, дерево решений и другие. Каждый метод имеет свои особенности и применяется в зависимости от конкретной задачи и требований.

Использование диаграмм множеств позволяет упростить и улучшить восприятие информации, делает ее более понятной и доступной. Они являются важным инструментом в процессе анализа и решения задач, а также помогают развивать навыки логического мышления и абстрактного мышления.

Примеры диаграмм множеств:

1. Диаграмма Венна:

2. Диаграмма пересечений:

В итоге, диаграмма множеств является важным инструментом для визуализации данных и представления логических связей между элементами множеств. Она помогает анализировать информацию, решать задачи и развивать мыслительные навыки.

Видео по теме:

Определение диаграммы множеств

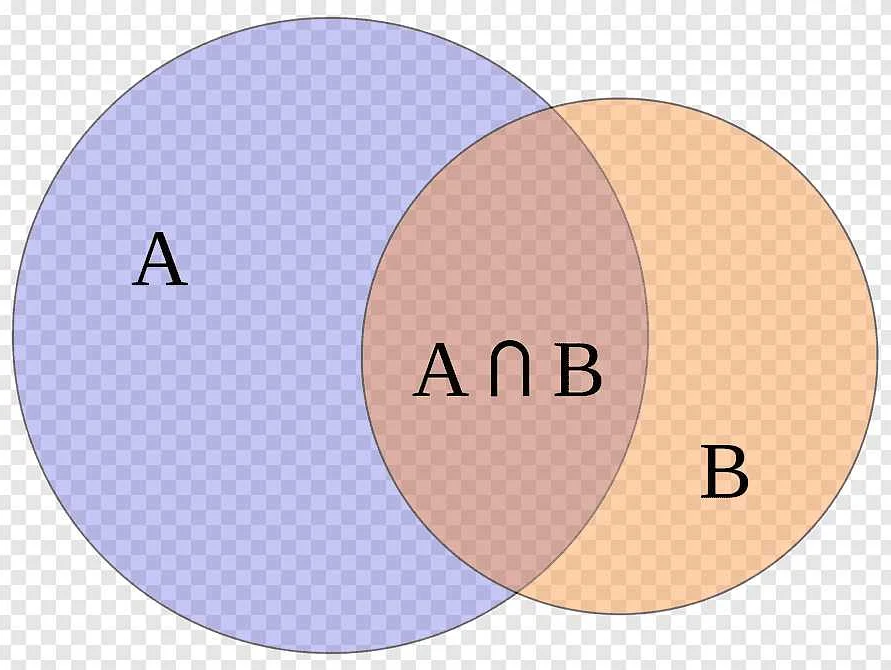
Диаграмма множеств помогает визуализировать и понять связи и зависимости между множествами. Она может быть использована для анализа и исследования различных областей, таких как логика, теория множеств, информатика и т.д.

В диаграммах множеств могут быть использованы различные символы и обозначения для обозначения отношений. Например, стрелки могут указывать на наличие элемента одного множества в другом множестве, а пересечения кругов – наличие общих элементов в разных множествах.

Диаграммы множеств являются эффективным инструментом для визуализации сложных отношений и структурных связей. Они позволяют легче понять и анализировать множества и их взаимодействия, а также упрощают решение различных задач и задач по построению алгоритмов.

Примеры диаграмм множеств

Вот несколько примеров диаграмм множеств:

Пример 1:

Рассмотрим два множества: A = {кот, собака, попугай} и B = {собака, хомяк}. Диаграмма множеств для данного примера будет выглядеть следующим образом:

Вставить диаграмму с овалами, представляющими множества A и B, и пересекающимися областями, обозначающими общие элементы.

Пример 2:

Рассмотрим три множества: A = {яблоко, груша, вишня}, B = {груша, виноград} и C = {вишня, апельсин}. Диаграмма множеств для данного примера будет выглядеть следующим образом:

Вставить диаграмму с овалами, представляющими множества A, B и C, и пересекающимися областями, обозначающими общие элементы.

Диаграммы множеств могут быть полезными инструментами в различных областях, таких как математика, логика, информатика и многие другие. Они позволяют легко визуализировать сложные отношения между множествами и облегчают понимание различных концепций.

Применение диаграмм множеств в математике

Одним из основных применений диаграмм множеств является изучение теории множеств. С помощью диаграмм можно показать отношения между различными множествами и операции над ними, такие как пересечение, объединение и разность. Это позволяет легче понять и запомнить основные понятия теории множеств.

Диаграммы множеств также применяются для решения задач, связанных с логикой и комбинаторикой. Они помогают наглядно представить возможные комбинации и пересечения элементов различных множеств, что упрощает решение задач и выявление закономерностей.

В более прикладных областях математики, таких как теория вероятностей и статистика, диаграммы множеств используются для представления вероятностных событий и их взаимосвязей. Например, с помощью диаграмм множеств можно проиллюстрировать вероятность пересечения двух или более событий.

В общем, диаграммы множеств позволяют визуализировать и анализировать сложные отношения между множествами, делая математические концепции более понятными и доступными.

Как строить диаграммы множеств

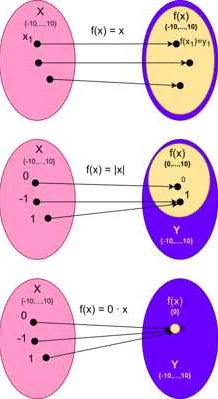
1. Определить множества, которые будут представлены в диаграмме. Каждое множество обычно представляется в виде круга или эллипса.
2. Определить элементы, принадлежащие каждому множеству. Элементы обычно указываются внутри кругов или эллипсов.
3. Определить отношения между множествами. Отношения могут быть представлены в виде стрелок или линий, соединяющих соответствующие элементы множеств.
4. Разместить множества и элементы на диаграмме в соответствии с определенными отношениями.
5. При необходимости добавить подписи к множествам или элементам для большей ясности и понимания.

Примеры диаграмм множеств могут включать отношения между различными категориями животных, предметами в классе или составляющими единицами в общей системе измерений.

Строительство диаграмм множеств является полезным инструментом для визуализации отношений и установления связей между различными множествами. Они помогают упростить сложные концепции и облегчить понимание математических и логических концепций.

Основные элементы диаграмм множеств

1	Множества	Это основные элементы диаграммы множеств. Они представлены в виде эллипсов или кругов и обозначаются буквами или символами. Каждое множество имеет свой уникальный символ.
2	Элементы	Элементы множества представлены внутри эллипса или круга, обозначающего соответствующее множество. Они также могут быть обозначены буквами или символами.
3	Отношения	Отношения между множествами представлены с помощью стрелок или линий, направленных от одного множества к другому. Они указывают на наличие связи или взаимодействия между множествами.
4	Пересечения	Пересечения множеств представлены перекрывающимися эллипсами или кругами. Они указывают на то, что у двух или более множеств есть общие элементы.
5	Объединения	Объединения множеств представлены объединяющими эллипсами или кругами. Они указывают на то, что два или более множества объединены и содержат все элементы из этих множеств.

Эти элементы позволяют визуально представить отношения между множествами и проиллюстрировать операции над множествами, такие как объединение, пересечение и разность.

Виды диаграмм множеств

Диаграмма Эйлера: это графическое представление множеств, где каждое множество изображается в виде круга или эллипса, а их пересечения показывают общие элементы.

Диаграмма Венна: это особый тип диаграммы Эйлера, где каждое множество изображается в виде круга или эллипса, а их пересечения показывают общие элементы. Диаграмма Венна часто используется для иллюстрации логических отношений и операций над множествами.

Диаграмма Мура: это графическое представление множеств, где каждое множество изображается в виде отрезка на числовой прямой, а их пересечения показывают общие элементы. Диаграмма Мура часто используется для иллюстрации отношений на числовой оси.

Диаграмма Карно: это графическое представление множеств, где каждое множество изображается в виде прямоугольника, а их пересечения показывают общие элементы. Диаграмма Карно часто используется в логике и теории множеств для решения задач с использованием операций над множествами.

Каждый из этих видов диаграмм множеств имеет свои особенности и применение в различных областях математики и логики.

Диаграммы множеств и логические операции

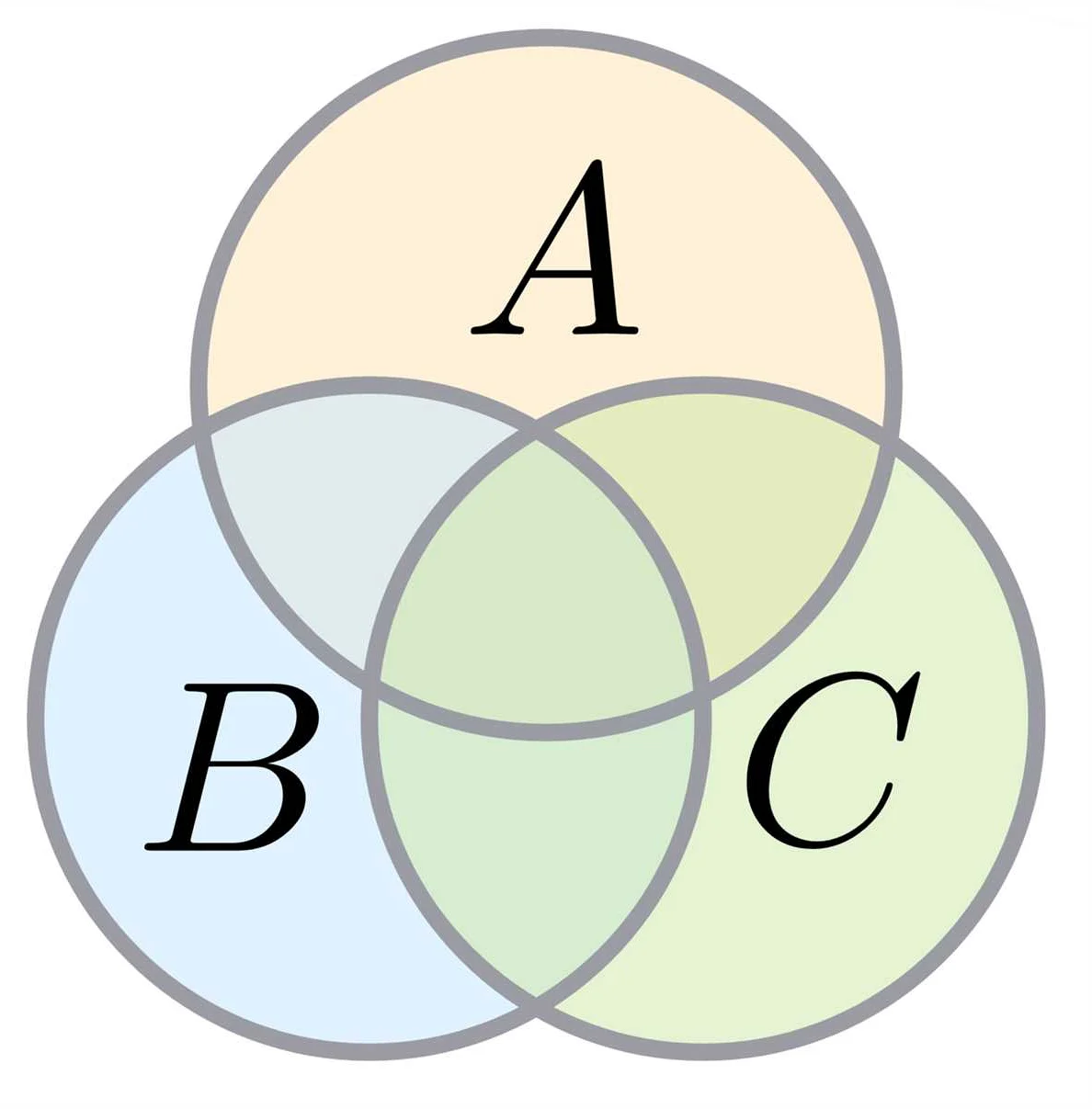
Диаграммы множеств в математике часто используются для визуализации отношений между различными множествами. Они представляют собой графическое изображение множеств и связей между ними. Кроме того, с помощью диаграмм множеств можно также выполнять различные логические операции.

Логические операции являются основой для работы с диаграммами множеств. Они позволяют комбинировать и модифицировать множества, исследовать их свойства и отношения. В основе логических операций лежат три основных операции: объединение, пересечение и разность.

Операция объединения позволяет объединить два или более множества в одно множество, включающее все элементы из исходных множеств. Обозначается символом «∪». Например, если есть два множества А = {1, 2, 3} и В = {3, 4, 5}, то их объединение будет выглядеть следующим образом: А ∪ В = {1, 2, 3, 4, 5}.

Операция пересечения позволяет найти общие элементы двух или более множеств. Обозначается символом «∩». Например, если есть два множества А = {1, 2, 3} и В = {3, 4, 5}, то их пересечение будет выглядеть следующим образом: А ∩ В = {3}.

Операция разности позволяет найти элементы, принадлежащие одному множеству, но не принадлежащие другому множеству. Обозначается символом » \ «. Например, если есть два множества А = {1, 2, 3} и В = {3, 4, 5}, то их разность будет выглядеть следующим образом: А \ В = {1, 2}.

Логические операции могут быть комбинированы и выполняться последовательно для получения более сложных результатов. Например, можно выполнить операцию пересечения с последующей операцией разности, чтобы найти элементы, принадлежащие одному множеству, но не принадлежащие другому множеству.

Диаграммы множеств и логические операции позволяют наглядно представить и анализировать отношения между множествами, отслеживать их пересечения и различия. Они являются мощным инструментом в математике и других областях, где требуется работа с множествами и логическими операциями.

Вопрос-ответ:

Что такое диаграмма множеств в математике?

Диаграмма множеств в математике — это графическое представление множеств и их отношений.

Какие примеры диаграмм множеств в математике существуют?

Примеры диаграмм множеств в математике: диаграмма Эйлера, диаграмма Венна, диаграмма Юнга и др.

Как применяются диаграммы множеств в математике?

Диаграммы множеств применяются для визуализации отношений между множествами, решения задач по теории множеств, логике и других областях математики.

Как использовать диаграмму множеств для определения пересечения множеств?

Для определения пересечения множеств на диаграмме множеств необходимо найти область перекрытия соответствующих кругов или эллипсов.

Можно ли использовать диаграммы множеств для представления более чем двух множеств?

Да, диаграммы множеств можно использовать для представления отношений между любым числом множеств. В этом случае используются соответствующие фигуры, например, пересекающиеся круги или эллипсы.

Что такое диаграмма множеств?

Диаграмма множеств — это графическое представление множеств и их отношений. Она помогает визуализировать связи между различными множествами.