Что такое множитель в математике 3 класс правило примеры

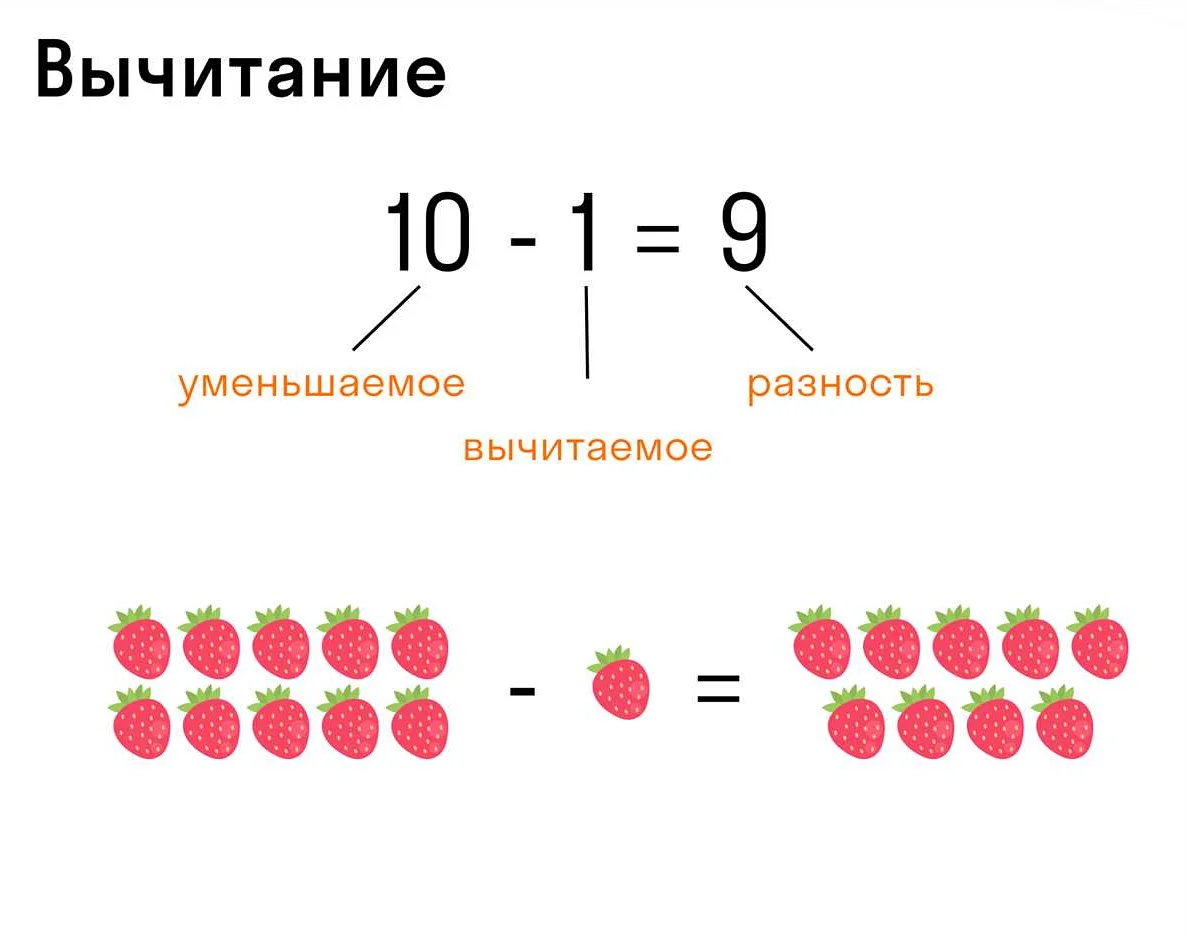
Множитель в математике 3 класса — это число, на которое умножают другое число. Узнайте правило умножения и примеры использования множителя в третьем классе.

Множитель – это число, на которое умножается другое число в математическом выражении. В третьем классе дети изучают операцию умножения и понятие множителя. Они учатся применять правило для нахождения произведения двух чисел.

Правило использования множителя в математике очень простое. Ребенок должен умножить число, на которое умножают, на число, на которое оно умножается. Например, если у нас есть задача: «Умножьте число 5 на 3», то ребенок должен умножить 5 на 3 и получить ответ 15.

Чтобы помочь детям лучше понять понятие множителя, учителя используют различные методы и примеры. Например, они могут предложить ребенку посчитать количество яблок в нескольких корзинах, где каждая корзина содержит одинаковое количество яблок. Ребенок должен посчитать, сколько яблок будет, если он возьмет несколько корзин и умножит количество яблок в каждой корзине на количество корзин.

Например, если в каждой корзине 4 яблока, а у ребенка есть 3 корзины, то он должен умножить 4 на 3 и получить ответ: 4 x 3 = 12.

Таким образом, использование множителя в математике позволяет детям научиться умножать числа и решать различные задачи. Это важный навык, который пригодится им не только в школе, но и в повседневной жизни.

Определение множителя

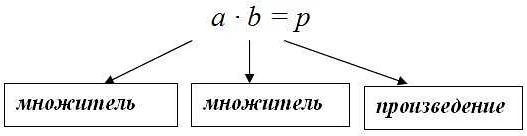
Множитель представляет собой число, на которое умножается другое число, называемое множимым. В умножении множитель всегда стоит перед множимым. Например, в уравнении 2 × 3 = 6, число 2 и число 3 — это множители, а число 6 — это их произведение.

Множитель может быть как целым числом, так и дробью. Если множитель является дробью, то перед умножением необходимо выполнить умножение числителя множителя на числитель множимого и знаменателя множителя на знаменатель множимого.

Например, при умножении дроби 1/2 на число 3, необходимо выполнить следующие действия: (1 × 3) / (2 × 1) = 3/2.

Знание понятия множителя играет важную роль в изучении математики и помогает понять, как умножать числа и решать различные математические задачи.

Правило использования множителя

Основное правило использования множителя заключается в умножении его на другое число или выражение. Для этого необходимо помнить следующие правила:

1. Умножение на ноль: Если один из множителей равен нулю, то результатом умножения будет ноль. Например: 0 * 5 = 0.

2. Умножение на единицу: Если один из множителей равен единице, то результатом умножения будет другой множитель. Например: 1 * 6 = 6.

3. Умножение на отрицательное число: Умножение на отрицательное число меняет знак результата. Если один из множителей отрицателен, то результатом будет отрицательное число. Например: (-3) * 4 = -12.

4. Умножение на переменные: При умножении на переменные, необходимо перемножить их коэффициенты (числа перед переменными) и сложить степени (если переменные имеют одинаковую степень). Например: 2x * 3x = 6x^2.

Правило использования множителя помогает производить умножение чисел и выражений с помощью учета основных правил и свойств. Это основа для решения множества задач и примеров в математике.

Примеры использования множителя

При решении задач с множителем, важно понимать, какое значение нужно присвоить множителю и умножаемому числу. Например, если решаем задачу о количестве яблок у 3 девочек, у каждой из которых есть по 4 яблока, то число 3 будет множителем, а число 4 – умножаемым.

Давайте рассмотрим несколько примеров использования множителя:

Пример 1: У Маши было 2 коробки, в каждой из которых лежало по 5 конфет. Сколько конфет было у Маши всего?

Решение: В данном примере у нас есть 2 коробки (множитель) и в каждой коробке лежит по 5 конфет (умножаемое). Чтобы найти общее количество конфет, нужно умножить 2 на 5: 2 × 5 = 10. Значит, у Маши было всего 10 конфет.

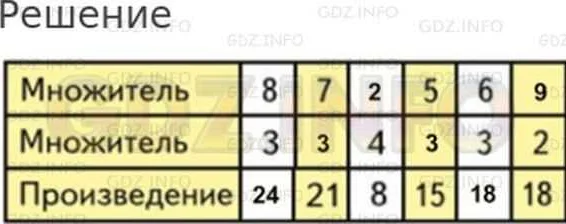
Пример 2: В магазине было 4 ряда по 6 яблок. Сколько яблок было в магазине?

Решение: В данном примере у нас есть 4 ряда (множитель) и в каждом ряду по 6 яблок (умножаемое). Чтобы найти общее количество яблок, нужно умножить 4 на 6: 4 × 6 = 24. Значит, в магазине было всего 24 яблока.

Таким образом, множитель используется для определения количества повторений или группировки элементов в задачах умножения. Он помогает находить общее количество объектов или величин, основываясь на количестве групп или повторений.

Как найти множитель в выражении?

Рассмотрим пример: выражение 3 * 7. В данном случае число 3 является множителем, так как оно умножается на число 7. Если в выражении есть несколько чисел или переменных, на которые происходит умножение, каждое из них будет являться отдельным множителем.

Также следует учитывать, что множитель может быть как положительным, так и отрицательным числом. Например, в выражении -2 * x число -2 является множителем, так как оно умножается на переменную x.

Для более сложных выражений, содержащих скобки и операции с переменными, необходимо следовать порядку выполнения операций. Найдите первое умножение в выражении и определите множитель, который участвует в этой операции.

Примеры выраженийМножитель

5 * 6	5
-3 * 4	-3
2 * x	2
(a + b) * 3	3

Таким образом, чтобы найти множитель в выражении, нужно определить число или переменную, на которую происходит умножение. В случае сложных выражений, следует учитывать правила выполнения операций и находить первое умножение в выражении.

Виды множителей

• Натуральные множители — это простые числа, на которые можно разложить данное число. Например, для числа 12 натуральными множителями являются 2 и 3, так как 12 = 2 * 2 * 3.
• Рациональные множители — это дроби или десятичные числа, на которые можно разложить данное число. Например, для числа 0.6 рациональными множителями являются 0.2 и 3, так как 0.6 = 0.2 * 3.
• Целые множители — это целые числа, на которые можно разложить данное число. Например, для числа 24 целыми множителями являются 2 и 12, так как 24 = 2 * 12.
• Отрицательные множители — это числа со знаком минус, на которые можно разложить данное число. Например, для числа -8 отрицательными множителями являются -1 и 8, так как -8 = -1 * 8.

Знание различных видов множителей позволяет ученикам лучше понимать процесс умножения и разложения чисел.

Значение множителя в уравнениях

Множитель в уравнениях играет важную роль. Он определяет, какое количество или сколько раз нужно умножить число или выражение. В уравнениях множитель обычно обозначается буквой a и стоит перед неизвестным числом.

Множитель можно использовать, чтобы найти значение неизвестного числа в уравнении. Например, если у нас есть уравнение a * 5 = 20, то мы можем найти значение неизвестного числа, разделив обе стороны уравнения на число 5. Таким образом, мы получим, что значение неизвестного числа равно 4.

Множитель также может быть использован для нахождения значения выражения или результата умножения. Например, если у нас есть уравнение 3 * b = 15, мы можем найти значение выражения, разделив обе стороны на число 3. В результате мы получим, что значение выражения равно 5.

Множитель может быть любым числом или выражением, которое можно умножить на другое число или выражение. Он может быть положительным, отрицательным, целым или десятичным числом. Важно понимать, что множитель изменяет значение числа или выражения в уравнении.

Использование множителя в уравнениях помогает нам решать различные математические задачи, включая нахождение неизвестных чисел, нахождение значений выражений и решение уравнений в целом. Поэтому важно понимать роль и значение множителя в математике.

Видео по теме:

Вопрос-ответ:

Какое значение имеет множитель в математике?

Множитель в математике — это число, на которое умножают другое число. Множитель определяет, сколько раз нужно взять данное число или объект. Например, в уравнении 3 * 4 = 12, число 3 является множителем, так как оно определяет, сколько раз нужно взять число 4.

Как правильно использовать множитель в математике?

Для использования множителя в математике нужно умножить его на другое число. Например, если есть уравнение 2 * 6, то нужно умножить число 2 на число 6, что даст результат равный 12. В данном случае, число 2 является множителем.

Как работает правило использования множителя в математике?

Правило использования множителя в математике простое: нужно умножить множитель на другое число. Если у нас есть уравнение 5 * 3, где 5 — множитель, а 3 — число, то мы должны умножить 5 на 3, что даст нам результат равный 15.

Какие примеры использования множителя можно привести?

Примеры использования множителя в математике могут быть разными. Например, умножение числа 4 на множитель 2 даст нам результат 8. Также, если у нас есть уравнение 6 * 5, то умножение множителя 6 на число 5 даст результат равный 30.

Какое значение множителя можно использовать в математике?

В математике можно использовать различные значения множителя. Это могут быть любые числа, как положительные, так и отрицательные. Например, можно умножить число 3 на -2, что даст результат -6. Также, можно использовать дробные числа в качестве множителя, например, умножение 2 на 0.5 даст результат 1.

Значение множителя в геометрии

Множитель в геометрии обычно используется для изменения размеров фигур. Он представляет собой коэффициент, на который умножается каждая измерительная линия или сторона фигуры.

Например, рассмотрим прямоугольник. Если у нас есть прямоугольник со сторонами 5 см и 3 см, и мы хотим увеличить его размеры в 2 раза, то мы можем использовать множитель 2. Умножая каждую сторону на множитель, получаем новые размеры прямоугольника — 10 см и 6 см.

Исходные размеры прямоугольникаНовые размеры прямоугольника

5 см	10 см
3 см	6 см

Множитель в геометрии может быть как положительным (увеличивает размеры фигуры), так и отрицательным (уменьшает размеры фигуры). Например, если мы возьмем множитель -0.5 и применим его к прямоугольнику со сторонами 6 см и 4 см, то получим новые размеры прямоугольника — 3 см и 2 см.

Исходные размеры прямоугольникаНовые размеры прямоугольника

6 см	3 см
4 см	2 см

Таким образом, множитель в геометрии играет важную роль в изменении размеров фигур и позволяет получить новые размеры путем применения заданного коэффициента к каждой измерительной линии или стороне фигуры.

Значение множителя в решении задач

При решении задач с множителем, необходимо понимать его значение и правильно применять его в вычислениях. Множитель может быть положительным или отрицательным числом, что влияет на результат.

Например, если у нас есть задача «Умножь число 4 на множитель 3», то результат будет 12. Здесь множитель 3 означает, что число 4 нужно умножить на 3, и мы получим число 12.

Если же множитель отрицательный, например, -2, то результат будет отрицательным. Например, в задаче «Умножь число 5 на множитель -2», результат будет -10. Здесь множитель -2 означает, что число 5 нужно умножить на -2, и мы получим число -10.

Значение множителя также может определять направление изменения числа. Например, если множитель равен 0.5, то результат умножения будет меньше исходного числа. Например, в задаче «Умножь число 8 на множитель 0.5», результат будет 4. Здесь множитель 0.5 означает, что число 8 нужно умножить на 0.5, и мы получим число 4, которое меньше 8.

Таким образом, понимание и правильное использование множителя в решении задач является важной частью математической грамотности и помогает нам получить правильные результаты.