Что такое множитель в математике 3

Множитель в математике 3 — это число, на которое умножается другое число. Узнайте, как использовать множитель в умножении и как решать задачи с его помощью.

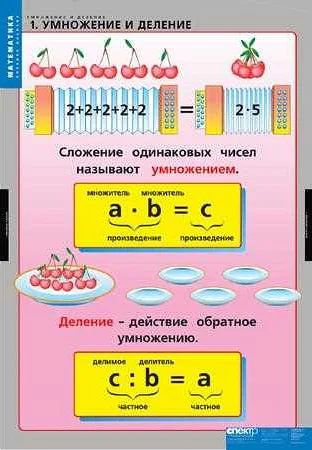
Множитель — одно из основных понятий в математике, используемое при выполнении операций умножения. Множитель представляет собой число или выражение, на которое умножается другое число или выражение, известное как множимое. Умножение выполняется путем повторения множимого на заданное количество раз, определенное множителем.

Примеры использования множителя в математике обычно включают числа и переменные. Например, в уравнении 3 * 4 = 12, число 3 и число 4 являются множителями, а число 12 — произведением этого умножения. В алгебре множители могут быть переменными, как, например, в уравнении x * y = z. Здесь x и y — множители, а z — произведение умножения.

Множитель может быть положительным, отрицательным или равным нулю. Знак множителя определяет, какой знак будет иметь произведение. Например, умножение положительного множителя на положительный приводит к положительному произведению, умножение отрицательного множителя на положительный — к отрицательному произведению, а умножение на ноль дает ноль.

Знание и понимание понятия множителя в математике является очень важным для решения различных уравнений и задач, использующих операцию умножения. Оно позволяет проводить вычисления с числами и переменными, а также анализировать различные свойства умножения, такие как коммутативность и дистрибутивность.

Что такое множитель в математике?

Множитель — это число, на которое умножается другое число, называемое множимым. В умножении множитель располагается слева от знака умножения и указывает, сколько раз нужно взять множимое. Например, в уравнении 3 х 4 = 12, число 3 является множителем, а число 4 — множимым.

Множители могут быть любыми числами: целыми или дробными, положительными или отрицательными. Они могут также быть переменными или выражениями. Например, в уравнении 2a х 5b = 10ab, выражения 2a и 5b являются множителями.

Множители в математике могут использоваться для решения различных задач и примеров. Например, они могут использоваться для нахождения площади прямоугольника или объема параллелепипеда. Они также могут использоваться для нахождения процента от числа или решения уравнений.

Важно помнить, что порядок множителей в умножении не влияет на результат. Например, 3 х 4 и 4 х 3 дадут одинаковый результат 12. Также важно учесть коммутативность умножения, что означает, что можно менять местами множители в умножении без изменения результата.

Видео по теме:

Определение множителя в математике

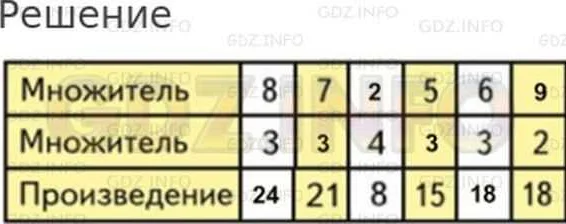
Множитель может быть представлен в виде числа или переменной. Если умножение включает несколько множителей, то каждый множитель умножается на произведение остальных множителей.

ПримерУмножимыеМножителиПроизведение

Умножение чисел	4 и 3	4, 3	12
Умножение переменных	x и y	x, y	xy
Умножение числа на переменную	5 и a	5, a	5a

Множитель играет важную роль в математических операциях, таких как умножение, деление и факторизация. Это понятие широко используется в алгебре, где множители могут быть положительными, отрицательными, рациональными или иррациональными числами.

Какие бывают множители?

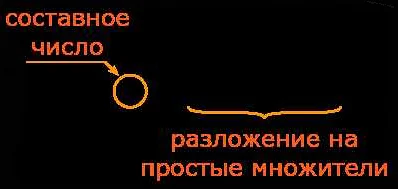
Основные типы множителей:

1. Простые множители — это числа, которые делятся только на себя и на единицу. Примерами простых множителей являются числа 2, 3, 5, 7 и т.д.
2. Составные множители — это числа, которые имеют более двух делителей. Они могут быть разложены на простые множители. Например, число 12 может быть разложено на простые множители: 2 * 2 * 3.
3. Алгебраические множители — это выражения, содержащие переменные и числа, их сочетания и операции умножения. Например, в выражении 2x * 3y, множители 2x и 3y являются алгебраическими множителями.

Множители могут использоваться в различных математических операциях, таких как умножение, факторизация и решение уравнений. Понимание различных типов множителей помогает в анализе и работе с числами и выражениями.

Как найти множитель в уравнении?

Для того чтобы найти множитель в уравнении, следует обратить внимание на знак перед переменной или выражением. Если переменная или выражение стоят без знака, то множителем является число 1. Если перед переменной или выражением стоит знак умножения, то множителем является число или выражение, стоящее перед знаком умножения.

Например, в уравнении 2x = 10, множителем является число 2, так как перед переменной x стоит знак умножения. В уравнении y + 3 = 7, множителем является число 1, так как перед переменной y нет знака умножения.

Иногда множителем может быть выражение, например, в уравнении (x + 2)(x — 3) = 0, множителими являются выражения x + 2 и x — 3. В таком случае, необходимо выполнить умножение указанных выражений, чтобы найти множитель.

Знание множителя в уравнении помогает определить возможные значения переменных или выражений и решить уравнение, используя различные методы и свойства математики.

Примеры использования множителя

Например, в выражении 3 * 4 = 12, число 3 является множителем, так как оно умножается на число 4.

Множитель также может использоваться для вычисления процентов. Например, если товар стоит 1000 рублей, а его цена увеличилась на 10%, то мы можем использовать множитель 1.1. Тогда новая цена будет равна 1000 * 1.1 = 1100 рублей.

Еще одним примером использования множителя является решение пропорций. Например, чтобы найти неизвестное значение x в пропорции 2/5 = x/10, мы можем использовать множитель 10/5, так как он позволяет умножить оба числа пропорции, чтобы получить равенство: (2/5) * (10/5) = x/10. Таким образом, x = 4.

В математических моделях множители часто используются для описания зависимости между величинами. Например, в модели экономики можно использовать множитель для описания, как изменение вложений в производство влияет на общий объем производства.

Значение множителя в умножении

Значение множителя имеет важное значение при выполнении умножения. Оно определяет, сколько раз нужно увеличить или уменьшить множимое. Например, если у нас есть уравнение 3 * 4, то первое число (3) будет множителем, а второе число (4) — множимым. Результатом будет число 12, так как мы увеличили 4 на 3 раза.

Множители также могут быть переменными или выражениями. В этом случае значение множителя может быть неизвестным или зависеть от других факторов. Например, в уравнении x * 5 = 20, мы не знаем значение переменной x, но можем выразить его, разделив обе стороны уравнения на 5. Таким образом, значение множителя играет ключевую роль в решении уравнений и вычислениях.

В математике множитель также может быть частью других операций, таких как деление и возведение в степень. В этих случаях значение множителя определяет, как производится операция и какой будет результат.

Использование правильных значений множителей в умножении является фундаментальной частью математического анализа и решения задач. Понимание значения множителя позволяет нам более точно определить результат умножения и использовать его в различных сферах нашей жизни, включая финансы, науку и технологии.

Множитель в делении: особенности

Особенностью множителя в делении является то, что он может быть равен нулю. В этом случае результат деления будет равен нулю. Например, если делимое число равно 8, а множитель равен 0, то результат деления будет равен 0.

Еще одной особенностью множителя в делении является его влияние на остаток. Если множитель равен 1, то остаток от деления будет равен 0. Если множитель больше 1, то остаток будет меньше делимого числа. Например, если делимое число равно 10, а множитель равен 3, то результат деления будет равен 3, а остаток – 1.

Важно помнить, что множитель в делении может быть как положительным, так и отрицательным числом. Знак множителя влияет на знак результат деления. Если множитель положителен, то результат деления будет также положительным. Если множитель отрицателен, то результат деления будет отрицательным.

Множитель в делении имеет большое значение при решении различных математических задач. Он позволяет находить не только частное, но и остаток от деления, а также выполнять дробные и десятичные деления.

Значение множителя в вычислениях

Множитель может быть как положительным, так и отрицательным числом, влияя на знак результата. Если множитель положителен, то результат умножения также будет положительным. Если множитель отрицателен, то результат будет иметь противоположный знак.

Например, если умножить число 5 на множитель 3, результат будет равен 15. Это означает, что число 5 увеличивается в 3 раза. Если же множитель будет отрицательным, например -3, результат умножения будет равен -15, то есть число 5 уменьшается в 3 раза.

Множитель также может быть равен 1 или 0. Если множитель равен 1, то умножение не изменяет значение множимого числа. Если множитель равен 0, то результат умножения всегда будет равен 0, независимо от значения множимого числа.

Значение множителя играет важную роль в различных математических операциях, таких как расширение скобок, нахождение произведения и решение уравнений. Понимание и правильное использование множителя позволяет выполнять точные и корректные вычисления.

Вопрос-ответ:

Что такое множитель в математике?

Множитель в математике — это число, на которое умножают другое число в процессе умножения. В уравнении a * b = c, a и b являются множителями, а c — их произведение.

Как определить множитель в уравнении?

Множитель в уравнении можно определить по тому, что он участвует в операции умножения. Если дано уравнение a * b = c, то a и b — это множители, а c — произведение.

Может ли множитель быть отрицательным числом?

Да, множитель может быть как положительным, так и отрицательным числом. Знак множителя определяет, в какую сторону будет изменяться произведение при умножении.

Можно ли умножить число на ноль?

Да, можно умножить число на ноль. В этом случае произведение будет равно нулю. Например, 5 * 0 = 0. В этом примере 5 — множитель, а 0 — нулевой множитель.

Какие примеры множителей можно привести?

Примеры множителей: 2 * 3 = 6, где 2 и 3 — множители, а 6 — их произведение; (-4) * 5 = -20, где (-4) и 5 — множители, а -20 — их произведение; 0 * 7 = 0, где 0 и 7 — множители, а 0 — нулевое произведение.