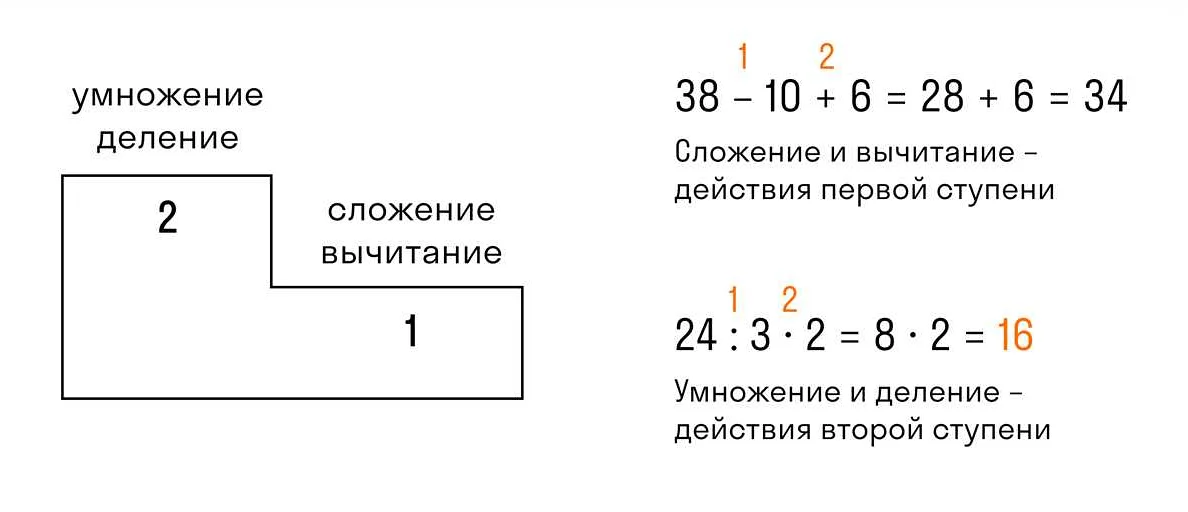
На больше какое действие в математике

Узнайте, на больше какое действие в математике помогает сравнивать числа и определять их отношение. Изучите основные принципы сравнения чисел и научитесь применять их в решении математических задач.

В математике существует множество методов и приемов, которые позволяют найти наибольшее значение функции или решить задачу с наибольшим результатом. Нахождение максимума в математике имеет важное значение во многих областях, таких как экономика, физика, инженерия и т. д. В этой статье мы рассмотрим несколько основных методов нахождения максимума функции и дадим практические примеры их применения.

Один из самых простых способов найти максимум функции — это метод проб и ошибок. Этот метод заключается в последовательном тестировании различных значений аргумента функции и вычислении соответствующего значения функции. Максимум функции будет соответствовать наибольшему значению, полученному в результате тестирования. Несмотря на свою простоту, этот метод может быть неэффективным, особенно для функций с большим количеством переменных или сложной структурой.

Более точные и эффективные методы нахождения максимума функции включают дифференцирование и оптимизацию. Дифференцирование позволяет найти производную функции, которая показывает ее скорость изменения в каждой точке. Максимум функции будет соответствовать точке, где производная равна нулю или не существует. Оптимизация, с другой стороны, представляет собой процесс поиска максимума функции с использованием различных алгоритмов и техник, таких как метод Монте-Карло, генетические алгоритмы и методы градиентного спуска.

В итоге, нахождение максимума функции — это важная задача, которая может быть решена с использованием различных методов и подходов. Выбор метода зависит от конкретной функции и условий задачи. Важно помнить, что нахождение максимума — это лишь первый шаг, а затем необходимо анализировать полученные результаты и применять их в реальных ситуациях.

Основные понятия и определения

1. Число — абстрактное понятие, обозначающее количество или порядок. Числа могут быть натуральными, целыми, рациональными или иррациональными.

2. Операции — математические действия, такие как сложение, вычитание, умножение и деление, которые позволяют выполнять различные математические операции.

3. Уравнение — математическое выражение, в котором две стороны равны друг другу. Решение уравнения — это нахождение значения переменной, при котором обе стороны уравнения равны.

4. Функция — математическое отображение, которое сопоставляет каждому элементу из одного множества элемент из другого множества. Функции могут быть линейными, квадратичными, тригонометрическими и т. д.

5. Дифференцирование — операция нахождения производной функции. Производная функции показывает, как быстро меняется значение функции в зависимости от изменения ее аргумента.

6. Интегрирование — операция нахождения интеграла функции. Интеграл функции позволяет определить площадь под графиком этой функции.

Это лишь некоторые из основных понятий и определений в математике. Их понимание и применение помогают в решении различных задач и построении математических моделей.

Методы нахождения наибольшего действия

Один из таких методов — метод дифференциального исчисления. С его помощью можно найти экстремумы функций. Для этого необходимо найти точки, в которых производная функции равна нулю, а затем проверить значение в этих точках.

Еще один метод — метод последовательных приближений. Он заключается в поиске последовательности приближенных значений действия, которая сходится к наибольшему действию. Этот метод широко используется в оптимизации и численных методах решения задач.

Также существуют различные алгоритмы и методы, разработанные специально для нахождения наибольшего действия в конкретных областях математики, таких как линейное программирование, дискретная оптимизация и другие.

Важно выбрать подходящий метод в зависимости от конкретной задачи и иметь необходимые навыки и знания для его применения. Это позволит найти наибольшее действие и получить точное и эффективное решение задачи.

Примеры задач на поиск наибольшего действия

Пример 1: Нахождение максимальной площади прямоугольника

Дана некоторая длина проволоки. Требуется с помощью этой проволоки построить прямоугольник с максимальной площадью. Какую ширину и длину должен иметь прямоугольник, чтобы площадь была максимальной?

Пример 2: Оптимальное размещение точек на плоскости

Дана некоторая область на плоскости и несколько точек, которые нужно разместить в этой области. Требуется найти такое размещение точек, чтобы сумма расстояний от каждой точки до остальных была минимальной. Какие координаты должны иметь точки для достижения этого результата?

Пример 3: Максимальное значение функции

Дана функция f(x), определенная на некотором интервале. Требуется найти такое значение x, при котором функция f(x) принимает максимальное значение. Какое значение x даст наибольшее значение функции?

Все эти задачи требуют анализа, вычислений и поиска оптимального решения. Нахождение наибольшего действия является важным инструментом в математике и широко применяется в различных областях.

Аналитическое решение задач на наибольшее действие

Аналитическое решение задач на наибольшее действие заключается в использовании принципа экстремальных значений. Для того чтобы найти наибольшее действие, нужно найти функцию, описывающую действие, и найти ее экстремальные значения.

Для начала, мы должны сформулировать задачу в математической форме. Затем, мы находим функцию, описывающую действие, и находим ее производную. Решив уравнение производной равной нулю, мы находим точки экстремума функции. Затем, мы проверяем, является ли найденная точка экстремума точкой максимума или минимума, сравнивая значение функции в этой точке с значениями функции в соседних точках.

При решении задач на наибольшее действие, необходимо учитывать ограничения задачи. Ограничения могут быть заданы в виде условий на значения переменных или в виде граничных условий. Их учет может потребовать использование метода множителей Лагранжа.

Аналитическое решение задач на наибольшее действие является важным инструментом для различных областей науки, включая оптику, механику и электромагнетизм. Применение этого принципа позволяет найти оптимальные решения и понять поведение физических систем.

Графическое решение задач на наибольшее действие

Для решения задачи с помощью графического метода нужно сначала построить график функции, описывающей действие, в координатной плоскости. Затем необходимо определить точку, в которой график функции достигает своего максимума или минимума. Эта точка будет являться решением задачи на наибольшее действие.

Для построения графика функции можно использовать различные методы, такие как построение таблицы значений, нахождение точек пересечения с осями координат, анализ поведения функции в окрестности особой точки и так далее. Важно учесть особенности каждой конкретной задачи и выбрать наиболее подходящий метод построения графика.

После построения графика функции необходимо найти точку на графике, в которой функция достигает своего максимального или минимального значения. Это можно сделать путем анализа наклона графика в окрестности точек перегиба или использования методов дифференциального исчисления для нахождения экстремумов функции.

Графическое решение задач на наибольшее действие позволяет наглядно представить результаты и сделать первоначальные выводы о решении задачи. Однако, в случае сложных функций и задач, может потребоваться использование дополнительных методов для точного нахождения решения.

Видео по теме:

Вопрос-ответ:

Какие методы можно использовать для поиска наибольшего действия в математике?

Для поиска наибольшего действия в математике можно использовать различные методы, например, методы оптимизации, методы динамического программирования, методы поиска с использованием графов, методы случайного перебора и другие.

Какие примеры задач могут быть решены с помощью поиска наибольшего действия в математике?

С помощью поиска наибольшего действия в математике можно решать различные задачи, такие как оптимизация функций, поиск наилучшего маршрута или планирование расписания, определение наибольшей возможной прибыли или наименьших затрат, а также другие задачи, связанные с максимизацией или минимизацией какого-либо показателя.

Какой метод является наиболее эффективным при поиске наибольшего действия в математике?

Эффективность метода при поиске наибольшего действия в математике зависит от конкретной задачи. Некоторые методы, такие как методы динамического программирования или методы оптимизации, могут быть эффективными во многих случаях, но в некоторых ситуациях может потребоваться применение более специализированных методов.

Какие навыки необходимы для решения задач по поиску наибольшего действия в математике?

Для решения задач по поиску наибольшего действия в математике необходимо иметь хорошее понимание математических концепций и методов, умение анализировать задачу и выбирать подходящий метод, а также умение программировать и использовать соответствующие математические инструменты и программные пакеты.

Как можно применить поиск наибольшего действия в математике в реальной жизни?

Поиск наибольшего действия в математике может быть применен в различных сферах реальной жизни. Например, в экономике он может использоваться для оптимизации процессов производства и распределения ресурсов, в логистике — для оптимизации маршрутов доставки, в финансовом анализе — для определения оптимального портфеля инвестиций, а также в многих других областях, где требуется максимизация или минимизация какого-либо показателя.

Какие методы используются для решения математических задач?

Для решения математических задач используются различные методы, в зависимости от конкретной задачи. Некоторые из них включают использование алгоритмов, применение формул и уравнений, применение графических методов и др. Важно выбрать подходящий метод в каждом конкретном случае и следовать последовательности шагов для достижения решения.

Можно ли найти решение для любой математической задачи?

В общем случае нельзя сказать, что для любой математической задачи существует решение. Некоторые задачи могут быть неразрешимыми или требовать использования достаточно сложных методов и алгоритмов. Однако, для большинства задач существуют методы и подходы, которые позволяют найти решение. Важно выбрать правильный подход и последовательно применять его для решения задачи.

Методы решения задач на наибольшее действие в экономике

Методы решения задач на наибольшее действие в экономике широко применяются для оптимизации производственных и инвестиционных процессов, а также для прогнозирования и планирования в экономической сфере. Данные методы основаны на применении математических моделей и алгоритмов для нахождения оптимального решения.

Одним из основных методов решения задач на наибольшее действие в экономике является метод динамического программирования. Этот метод позволяет разбить сложную задачу на более простые подзадачи, решение которых затем комбинируется для получения оптимального результата. Динамическое программирование позволяет учесть ограничения и условия задачи, а также учитывает взаимосвязи между различными переменными и факторами.

Еще одним методом решения задач на наибольшее действие в экономике является метод математического программирования. В рамках этого метода задача формулируется как математическая модель с определенными целевыми функциями и ограничениями. Затем используются методы линейного, нелинейного или динамического программирования для нахождения оптимального решения. Метод математического программирования широко применяется в экономической теории, финансах, логистике и других областях экономики.

Также существуют различные эвристические методы решения задач на наибольшее действие в экономике. Эти методы основаны на опыте и интуитивном понимании проблемы, и позволяют получить приближенное оптимальное решение. Примерами эвристических методов являются методы искусственного интеллекта, генетические алгоритмы и методы имитации отжига.

Все эти методы решения задач на наибольшее действие в экономике имеют свои преимущества и ограничения, и выбор конкретного метода зависит от сложности задачи, наличия данных и требуемой точности результата. Комбинирование различных методов позволяет получить более точные и надежные решения в экономической сфере.

Применение наибольшего действия в науке и технике

В науке, наибольшее действие используется для оптимизации различных процессов и систем. Например, в физике оно применяется для определения наиболее эффективных траекторий движения объектов или для нахождения наиболее стабильного состояния системы. В химии наибольшее действие может помочь определить оптимальные условия реакции и выбрать наиболее эффективный катализатор.

В технике наибольшее действие используется для решения различных задач проектирования и оптимизации. Например, в инженерии наибольшее действие может помочь определить оптимальные размеры и форму конструкции, чтобы она была максимально прочной и эффективной. В информационных технологиях наибольшее действие применяется для оптимизации алгоритмов и поиска наилучших решений.

В целом, наибольшее действие является важным инструментом для нахождения оптимальных решений в различных областях науки и техники. Благодаря этому понятию удается достигать максимальной эффективности и оптимизации процессов, что является основой для развития и прогресса в научных и технических областях.