Что такое неравенства в математике

Неравенства в математике – это математические выражения, в которых сравниваются два или более числа или переменных. В статье рассмотрены основные виды неравенств, их свойства и способы решения. Познакомьтесь с этой важной темой математики и узнайте, как использовать неравенства для решения различных задач и уравнений.

Неравенства являются одним из важных понятий в математике. Они представляют собой высказывания о неравенстве двух выражений или чисел. Неравенство может быть записано с использованием таких математических символов, как «» (больше), «≤» (меньше или равно) и «≥» (больше или равно).

В математике неравенства используются для сравнения и установления отношений между числами. Они позволяют сравнивать числа на основе их величины и порядка. Например, неравенство 2 > 1 говорит нам о том, что число 2 больше числа 1.

Основными правилами работы с неравенствами являются:

1. Прибавление или вычитание числа из обеих частей неравенства не меняет его направления.

Например, если дано неравенство a > b, то прибавление или вычитание одного и того же числа из обеих частей неравенства не меняет его значение. Так, прибавление числа c к обеим частям неравенства не изменит его направления: a + c > b + c.

2. Умножение или деление обеих частей неравенства на положительное число не меняет его направления.

Например, если дано неравенство a > b и положительное число c, то умножение или деление обеих частей неравенства на положительное число c не изменит его значение. Так, умножение обеих частей неравенства на положительное число c не изменит его направления: ac > bc.

3. Умножение или деление обеих частей неравенства на отрицательное число меняет его направление.

Например, если дано неравенство a > b и отрицательное число c, то умножение или деление обеих частей неравенства на отрицательное число c изменит его значение и направление. Так, умножение обеих частей неравенства на отрицательное число c изменит его направление: ac < bc.

Что такое неравенства в математике?

Неравенства в математике используются для сравнения различных значений, определения диапазонов чисел или переменных и решения различных задач. Они играют важную роль в алгебре, геометрии, математическом анализе и других разделах математики.

Примеры неравенств:

1. 5 < 8 – это неравенство утверждает, что число 5 меньше числа 8.

2. x + 3 > 10 – это неравенство содержит переменную x и утверждает, что значение x, увеличенное на 3, больше 10.

3. 2x — 4 ≤ 10 – это неравенство содержит переменную x и утверждает, что значение 2x, уменьшенное на 4, не превосходит 10.

Важно помнить, что неравенства могут иметь различные решения в зависимости от входящих в них переменных и значений. При решении неравенств необходимо учитывать основные правила, которые позволяют преобразовывать и упрощать неравенства.

Основные правила неравенств в математике

В математике неравенства играют важную роль при сравнении чисел и выражений. Они помогают определить, какое из двух чисел больше или меньше.

Основные правила неравенств в математике включают:

1. 1. Правило сложения и вычитания

Если к обоим сторонам неравенства добавить или вычесть одно и то же число, то неравенство сохраняет свою справедливость. Например:

1. 1. • Если a > b, то a + c > b + c
      • Если a > b, то a — c > b — c
   2. Правило умножения и деления на положительное число

Если обе стороны неравенства умножить или разделить на положительное число, то неравенство сохраняет свою справедливость. Например:

1. 1. • Если a > b и c > 0, то a * c > b * c
      • Если a > b и c > 0, то a / c > b / c
   2. Правило умножения и деления на отрицательное число

Если обе стороны неравенства умножить или разделить на отрицательное число, то неравенство меняет свое направление. Например:

1. 1. • Если a > b и c < 0, то a * c < b * c
      • Если a > b и c < 0, то a / c < b / c
   2. Правило смены знака

Если обе стороны неравенства поменять местами и знаки, то неравенство сохраняет свою справедливость. Например:

1. • Если a > b, то -a < -b

Правила неравенств в математике помогают решать уравнения, неравенства и задачи, связанные с сравнением чисел и выражений.

Сравнение чисел

Для сравнения чисел используются математические символы, называемые знаками сравнения. В таблице ниже приведены наиболее часто используемые знаки сравнения и их значения:

Знак сравненияОписаниеПример

	Меньше	3 < 5
>	Больше	5 > 3
≤	Меньше или равно	3 ≤ 5
≥	Больше или равно	5 ≥ 3
=	Равно	3 = 3

Правила сравнения чисел:

• Если число A больше числа B, то A > B.
• Если число A меньше числа B, то A < B.
• Если число A равно числу B, то A = B.
• Если число A меньше или равно числу B, то A ≤ B.
• Если число A больше или равно числу B, то A ≥ B.

Сравнение чисел широко применяется в решении математических задач, а также в других областях науки и повседневной жизни.

Решение неравенств в одной переменной

Для решения неравенств в одной переменной следует выполнить определенные шаги:

1. Перенести все члены неравенства на одну сторону уравнения так, чтобы ноль оказался на другой стороне.
2. Сократить подобные члены и упростить выражение.
3. Определить интервалы, в которых переменная удовлетворяет неравенству, используя знаки неравенства.

Полученные интервалы являются решением неравенства. Они могут быть представлены в виде отрезков на числовой прямой или записаны в виде интервальной записи.

Важно помнить, что при умножении или делении неравенства на отрицательное число, необходимо изменить направление неравенства.

Решение систем неравенств

Основной метод решения систем неравенств — графический метод. Сначала нужно построить графики всех неравенств и найти область, в которой пересекаются все графики. Затем определяем значения переменных в этой области, которые удовлетворяют всем неравенствам.

Если система состоит из двух неравенств, графический метод сводится к нахождению области пересечения двух графиков. Если система состоит из трех и более неравенств, то область пересечения графиков нужно находить последовательно.

При решении систем неравенств важно помнить о правилах знаков. Если в системе присутствуют неравенства с знаком , то значения переменных должны быть больше указанного числа. Если в системе присутствуют неравенства с знаком ≤ или ≥, то значения переменных должны быть меньше или равны, либо больше или равны указанному числу соответственно.

Решение системы неравенств может иметь несколько видов: пустое множество (когда область пересечения графиков не существует), множество, состоящее из одной точки (когда область пересечения графиков существует и состоит только из одной точки), полубесконечное множество (когда область пересечения графиков представляет собой полубесконечность) или бесконечное множество (когда область пересечения графиков представляет собой всю числовую прямую).

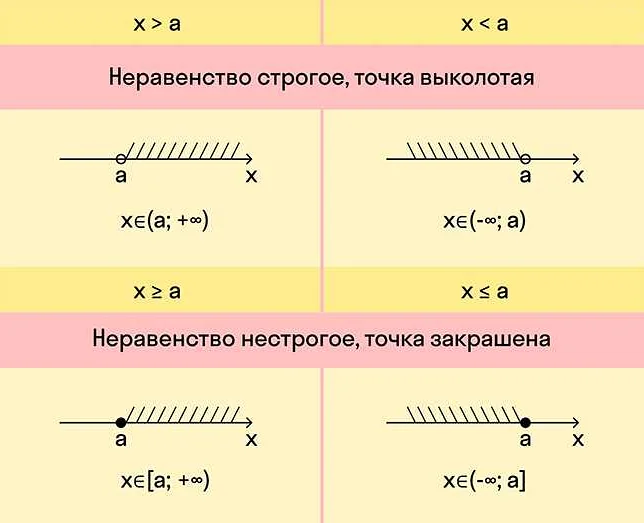
Графическое представление неравенств

Неравенства в математике можно представить графически на координатной плоскости. Для этого необходимо знать, как изобразить линию, соответствующую уравнению. Затем, в зависимости от типа неравенства, нужно определить, каким образом будет закрашиваться область, удовлетворяющая неравенству.

Для неравенств сравнения типа «больше» или «меньше» используется сплошная линия. Если неравенство включает «больше или равно» или «меньше или равно», то используется прерывистая линия.

После того, как линия нарисована, нужно определить, какую область нужно закрасить. Для этого проверяют неравенство на точке, которая лежит на одной стороне от линии. Если неравенство выполняется, то закрашивают область, содержащую эту точку. Если неравенство не выполняется, то закрашивают область, не содержащую эту точку.

Для наглядности и удобства можно использовать таблицу, в которой указываются значения координат и проверяется выполнение неравенства для каждой точки.

xyНеравенствоВыполняется?

0	0	x + y < 5	Да
3	2	x + y < 5	Нет

Таким образом, графическое представление неравенств позволяет наглядно представить область, удовлетворяющую неравенству, и тем самым облегчает решение задач и анализ математических моделей.

Применение неравенств в реальной жизни

Неравенства в математике имеют широкое применение в реальной жизни. Они позволяют нам сравнивать и описывать различные величины и отношения между ними. Неравенства используются в различных областях, включая экономику, физику, социологию и многие другие.

В экономике неравенства позволяют описывать отношения между доходами и расходами, рыночными ценами и спросом, а также другими экономическими параметрами. Например, если у вас есть ограниченный бюджет, неравенства помогут вам определить, сколько вы можете потратить на различные товары или услуги.

В физике неравенства используются для описания отношения между различными физическими величинами, такими как сила, скорость, ускорение и другие. Например, законы Ньютона формулируются с использованием неравенств и позволяют определить, какие силы будут действовать на тело в зависимости от его массы и ускорения.

В социологии неравенства помогают описывать и анализировать социальные отношения, различия в благосостоянии, образовании и доступе к ресурсам. Например, неравенства доходов позволяют изучать распределение богатства в обществе и выявлять причины и последствия социальных неравенств.

Таким образом, применение неравенств в реальной жизни помогает нам анализировать и описывать различные отношения и величины, а также принимать рациональные решения на основе этих неравенств.

Важность понимания неравенств в математике

Неравенства в математике позволяют нам определить отношение между двумя числами или выражениями. Они могут быть использованы для сравнения чисел по их значениям, например, для определения, какое число больше или меньше. Также неравенства позволяют нам сравнивать выражения, содержащие переменные, и определять условия, при которых они будут верными.

Понимание неравенств важно для решения различных задач и уравнений. Они позволяют нам определить интервалы значений, в которых переменная может находиться, и решить неравенство для определения этих интервалов. Неравенства также используются в математическом моделировании, статистике, экономике и других областях, где требуется определить отношение между переменными или ограничить значения переменных.

Основные правила работы с неравенствами включают в себя операции сравнения, такие как сложение, вычитание, умножение и деление. Понимание этих правил позволяет нам решать неравенства и находить значения переменных, удовлетворяющие данным условиям.

ОперацияПравило

Сложение/вычитание	Если к обеим частям неравенства прибавить/вычесть одно и то же число, неравенство не изменится.
Умножение/деление на положительное число	Если обе части неравенства умножить/разделить на положительное число, неравенство не изменится.
Умножение/деление на отрицательное число	Если обе части неравенства умножить/разделить на отрицательное число, неравенство изменит направление.

Понимание этих правил позволяет нам легче анализировать и решать неравенства, а также использовать их в других математических и научных областях.

Вопрос-ответ:

Что такое неравенство в математике?

Неравенство в математике это выражение, в котором указывается, что два числа не равны друг другу. Одно из чисел может быть больше или меньше другого.

Какие основные правила справедливы для неравенств?

Основные правила для неравенств включают в себя правила сложения и вычитания, умножения и деления на положительные и отрицательные числа.

Какие символы используются в неравенствах?

В неравенствах используются символы «>», «», означает «больше», »

Как решать неравенства с переменными?

Чтобы решить неравенство с переменными, нужно использовать те же правила, что и для решения неравенств с числами. Нужно выразить переменную, провести операции и найти интервалы, в которых переменная может находиться.

Что такое решение неравенства?

Решение неравенства — это интервал, в котором находятся значения переменной, удовлетворяющие данному неравенству. Например, решение неравенства «x > 3» будет интервал (-бесконечность, 3).

Видео по теме: