Какие категории входят в математическое содержание: полный список и объяснения

Статья разбирает различные категории, входящие в область математического содержания, такие как алгебра, геометрия, теория вероятности, статистика и другие. Изучение и понимание этих категорий важно для любого студента математики и поможет им в решении задач и создании новых математических теорий.

Математика — одна из научных дисциплин, которая изучает структуру, свойства и взаимосвязь различных объектов и явлений. Область её математического содержания объединяет разнообразные категории и виды, каждый из которых имеет свои особенности и применяется в конкретных областях знаний.

Одной из основных категорий математического содержания является алгебра, которая изучает свойства алгебраических систем, операции и их свойства. В математике существуют различные виды алгебры, такие как линейная, абстрактная, групповая, кольцевая и прочие, которые широко применяются в физике, экономике и других науках.

Еще одной важной категорией математического содержания является геометрия, которая изучает форму, размер и положение геометрических объектов. Существуют разные виды геометрии, например, евклидова, неевклидова, дифференциальная, пространственная и др. Геометрия используется в разных областях науки, включая архитектуру, инженерию, физику и компьютерную графику.

Кроме того, математическое содержание включает в себя такие категории, как анализ, топология, комбинаторика и др. Каждая из них имеет свои собственные виды, которые занимают центральное место в математических исследованиях и имеют широкий спектр применения в науке, технологиях и других областях.

Математические объекты и операции

В математике существуют различные объекты, которые являются базовыми единицами изучения. Среди них можно выделить числа, функции, векторы, матрицы, графы и множества. Каждый из этих объектов имеет свои особенности и свойства, которые изучаются в рамках различных ветвей математики.

Числа являются одним из наиболее простых и распространенных объектов в математике. Их можно разделить на натуральные, целые, рациональные и действительные. Кроме того, существуют комплексные числа, которые содержат в себе действительную и мнимую части. Числа используются для описания количественных характеристик и для выполнения арифметических операций, таких как сложение, вычитание, умножение и деление.

Функции представляют собой отображения между множествами. Они могут быть заданы аналитически или графически и могут быть одномерными или многомерными. Функции используются для моделирования различных явлений в науке и технике, а также для решения задач в математическом анализе и других областях.

Векторы и матрицы — это объекты, используемые в линейной алгебре. Векторы представляют собой направление и величину, а матрицы — таблицу чисел. Они используются для решения систем линейных уравнений, построения пространственных моделей и обработки изображений.

Графы — это объекты, состоящие из вершин и ребер, которые используются для моделирования связей между объектами. Графы используются в теории графов, теории алгоритмов и других областях.

Множества — это совокупность объектов, которые удовлетворяют определенному свойству. Они используются в теории множеств, теории вероятностей и других областях математики.

Операции выполняются над объектами и позволяют получать новые объекты. Среди операций можно выделить арифметические, логические, отношения и трансцендентные. Арифметические операции выполняются над числами, логические — над утверждениями, отношения — над множествами, а трансцендентные — над функциями.

Таким образом, математические объекты и операции являются основой математики и используются в различных областях науки и техники.

Алгебраические системы и их свойства

Алгебраическая система — это непустое множество, на котором заданы операции, удовлетворяющие определенным аксиомам. Основными свойствами алгебраических систем являются замкнутость, ассоциативность и существование нейтральных и обратных элементов.

Примерами алгебраических систем являются группы, полукольца, кольца, поля и другие. Группы — это алгебраические системы, удовлетворяющие определенным аксиомам, которые позволяют выполнять операции сложения и умножения. Полукольца и кольца — это алгебраические системы, в которых расширяется возможность выполнения арифметических операций. Поля — это алгебраические системы, обладающие особыми свойствами.

Одно из важнейших свойств алгебраических систем — дистрибутивность. Она представляет собой закон, который связывает выполнение операции умножения с операцией сложения. Дистрибутивность играет ключевую роль в алгебраических системах и используется при решении многих задач.

Алгебраические системы и их свойства имеют широкое применение в различных областях науки и техники, включая математику, физику, экономику, информатику и другие. Знание этих систем и их свойств помогает в решении сложных задач и создания новых предметов и технологий.

Аналитическая геометрия и оптимизация

Аналитическая геометрия — это раздел математики, изучающий свойства геометрических объектов с помощью алгебраических методов. Она позволяет описывать и анализировать геометрические фигуры в многомерном пространстве с помощью алгебраических уравнений.

Одной из важных применений аналитической геометрии является оптимизация. Она позволяет искать экстремумы функций с использованием графических методов, что позволяет найти точки минимума и максимума функций и решить задачи оптимизации.

В оптимизации часто используются методы многомерного анализа, такие как методы градиентного спуска и методы Ньютона. Они позволяют быстро находить оптимальные решения для сложных проблем.

• Применение аналитической геометрии и оптимизации может быть найдено в различных областях, таких как экономика, физика, техника и т.д.
• Аналитическая геометрия и оптимизация также широко используются в компьютерной графике и компьютерном моделировании, где они позволяют создавать сложные трехмерные модели.

В современном мире аналитическая геометрия и оптимизация имеют огромное значение во всех областях и являются неотъемлемой частью науки и технологий.

Теория чисел и ее приложения

Теория чисел — это отрасль математики, изучающая свойства и законы целых чисел. Она занимается решением таких задач, как простые числа, делимость, модульная арифметика, диофантовы уравнения, теория цепных дробей и другие.

Теория чисел является фундаментальной областью математики, которая имеет множество приложений в науке и технике. Она находит применение в криптографии, теории кодирования, математическом моделировании, теории вероятностей, финансовой математике и многих других областях.

Криптография — это наука о методах защиты информации. Фундамент отрасли лежит в математической теории кодирования и теории чисел. Одним из примеров применения теории чисел в криптографии является RSA-алгоритм, который используется для шифрования и подписи электронных документов.

Теория кодирования — наука о методах кодирования информации для ее передачи и хранения. Она тесно связана с теорией чисел и использует ее результаты для создания эффективных и надежных кодов. Одним из приложений теории кодирования являются беспроводные сети связи и спутниковые связи.

Математическое моделирование — это процесс создания математической модели для изучения свойств изучаемой системы. Теория чисел является необходимой для создания и анализа моделей в различных областях, таких как экономика, физика, биология и другие.

Финансовая математика — это наука о методах оценки финансовых рисков и вычисления стоимости различных финансовых инструментов. Она широко использует результаты теории чисел для создания эффективных моделей оценки финансовых инструментов и минимизацию рисков.

Таким образом, теория чисел и ее приложения являются важной частью современной науки и техники. Они находят применение в различных областях и предоставляют возможности для новых научных и технологических достижений.

Геометрические пространства и их свойства

Геометрическое пространство — это абстрактное математическое понятие, которое описывает физическую топологию объекта. В математике существует несколько видов геометрических пространств: евклидово, проективное, сферическое, гиперболическое и многомерное.

Евклидово пространство — это наиболее распространенный тип геометрического пространства, в котором действуют обычные законы геометрии. Евклидовым пространством может быть, например, лист бумаги или поверхность стола. Его свойства описываются аксиомами Евклида.

Проективное пространство — это пространство, в котором существует бесконечно удаленная точка, и все параллельные прямые пересекаются в этой точке. Также в проективном пространстве не существует определенных отрезков и углов, они заменяются на эквивалентные отношения между точками.

Сферическое пространство — это пространство на поверхности сферы, его свойства сильно отличаются от свойств евклидового пространства. Например, в сферическом пространстве сумма углов треугольника может быть больше 180 градусов. Сферическое пространство используется в геодезии и астрономии.

Гиперболическое пространство — это пространство, в котором все прямые кривые, а углы между прямыми меньше 90 градусов. Это противоположность евклидовому пространству, где углы между прямыми равны 90 градусов. Гиперболическое пространство используется в теории относительности и теории хаоса.

Многомерное пространство — это общее название для геометрических пространств больше трех размеров.

В заключение, геометрические пространства имеют свои уникальные свойства и используются в различных областях математики и науки.

Дифференциальные уравнения и их решения

Дифференциальное уравнение (ДУ) — уравнение, связывающее функцию нескольких переменных с её производными. Решение ДУ — это функция, которая удовлетворяет уравнению и заданным начальным условиям. ДУ применяются во многих областях науки и техники, таких как физика, химия, экономика, биология и т.д.

В зависимости от числа переменных, на которые зависит неизвестная функция и её производные, ДУ могут быть обыкновенными (ОДУ) или частными (ЧДУ). ОДУ содержат только одну независимую переменную, ЧДУ содержат несколько независимых переменных.

Методы решения ДУ могут быть аналитическими или численными. Аналитические методы позволяют получить решение в явном виде, используя математические методы и формулы. Численные методы позволяют получить приближенное значение решения, используя численные алгоритмы и компьютерные вычисления.

• К аналитическим методам относятся: метод разделения переменных, метод интегрирующего множителя, метод неопределенных коэффициентов, метод вариации постоянных и т.д.
• К численным методам относятся: метод Эйлера, метод Рунге-Кутта, метод конечных разностей, метод элементов и т.д.

Решение ДУ должно удовлетворять начальным условиям, которые могут быть заданы в виде значений неизвестной функции и её производных в некоторой точке. Например, начальное условие для ОДУ может быть задано в виде значения функции и её производной в точке x0.

Тип ДУПримеры уравнений

ОДУ первого порядка	y’ = f(x,y)
ОДУ n-го порядка	y⁽ⁿ⁾ = f(x,y,y’,…,y⁽ⁿ⁻¹⁾)
ЧДУ первого порядка	uₓ + vₓₓ + wₓₓₓ = f(x,y,u,v,w)
ЧДУ n-го порядка	u₁₂₃…ₙ + v₁₂₃…ₙ + … + w₁₂₃…ₙ = f(x,y,u₁,u₂,…,wₙ)

Теория вероятностей и статистика

Теория вероятностей и статистика являются одной из основных областей математики и применяются практически во всех сферах жизни, от науки и техники до бизнеса и финансов. Теория вероятностей изучает случайные явления, определяет вероятность их возникновения и позволяет прогнозировать результаты будущих событий.

Статистика же занимается сбором, анализом и интерпретацией данных, которые могут быть получены в результате наблюдений или экспериментов. Кроме того, статистика позволяет выделять закономерности, связи и тенденции в данных.

Основные понятия теории вероятностей, такие как событие, вероятность, случайная величина, математическое ожидание и дисперсия, используются во многих областях, включая физику, экономику, социологию и другие науки.

Статистика же позволяет ставить и решать задачи по обработке и анализу данных, а также проверке гипотез и прогнозированию будущих трендов. Без теории вероятностей и статистики невозможно представить современную науку и бизнес.

Теория графов и ее применения

Теория графов – это раздел математики, изучающий свойства и структуры графов. Графом называется математический объект, состоящий из вершин и ребер, которые соединяют эти вершины. Теория графов имеет много приложений в различных областях науки и техники: от компьютерной науки и информатики до транспортной логистики и социологии.

Применения теории графов:

1. Сетевое планирование и управление проектами: графы используются для моделирования и планирования проектов, определения критических путей и управления ресурсами. Это особенно важно в индустрии строительства, где проекты могут быть очень сложными и длительными.
2. Обработка данных: графы часто используются для представления и анализа данных, таких как социальные сети, сценарии игр или маршруты путешествий. Это позволяет осуществлять более эффективную обработку данных и получать ценную информацию из больших объемов данных.
3. Транспортный дизайн и логистика: графы широко используются для проектирования и оптимизации транспортных сетей, таких как дороги, морские пути или авиалинии. Это помогает снизить затраты на транспортировку товаров и улучшить доступность транспортной инфраструктуры.
4. Комбинаторика: графы играют ключевую роль в комбинаторике, области математики, изучающей различные комбинаторные структуры, такие как перестановки или сочетания. Комбинаторика имеет множество приложений в криптографии, теории кодирования или теории алгоритмов.

Заключение:

Все вышеперечисленные области являются лишь некоторыми из многих областей, где теория графов имеет значительное приложение. Это делает теорию графов важным разделом математики, имеющим очень широкое применение в реальном мире.

Математическая логика и ее свойства

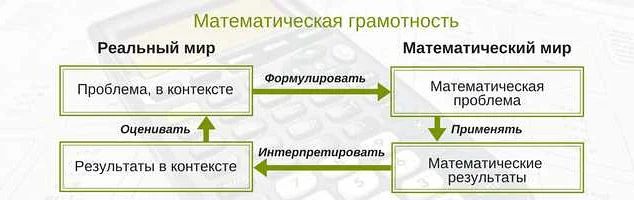
Математическая логика — это раздел математики, который изучает формальные языки, символические системы и методы рассуждений, используемые для изучения логических и математических проблем. Она также является инструментом для формализации и доказательства математических теорем.

Одной из главных целей математической логики является формализация логических выражений и применение математических методов для доказательства формальных утверждений. Ее методы включают аксиоматику, доказательства, конечные и бесконечные множества, теорию вычислимости, алгебры булевых функций и другие математические техники.

Одним из свойств математической логики является возможность использования ее методов во многих областях науки и техники, включая информатику, физику, инженерию и другие дисциплины. Она также помогает устанавливать формальные правила для рассуждений, что позволяет избегать ошибок и создавать точные и строгие аргументы.

Выводы, сделанные с помощью формальных методов математической логики, могут быть не только точными, но и экономичными, поскольку они позволяют получать результаты с помощью минимального количества утверждений и доказательств. Более того, они могут быть применимы не только в академической сфере, но и в повседневной жизни, например, при проектировании систем автоматизации или при разработке программного обеспечения.

Видео по теме:

Вопрос-ответ:

Что такое область математического содержания?

Область математического содержания — это совокупность знаний, которые необходимы для изучения математической теории, обеспечивающие ее понимание и применение в решении различных задач.

Какие категории входят в область математического содержания?

Категории, входящие в область математического содержания, могут различаться в зависимости от уровня образования. К ним относятся, например, элементы математической логики, теория множеств, алгебра, геометрия, теория вероятностей и другие.

Какие виды математического содержания существуют?

В зависимости от уровня сложности и специализации, можно выделить такие виды математического содержания, как базовые понятия и определения, теоремы и доказательства, приложения математических знаний в различных областях науки и техники.

Какие навыки нужно иметь для успешного изучения области математического содержания?

Для успешного изучения области математического содержания необходимо иметь навыки анализа, логического мышления, абстрагирования и моделирования. Также важным является умение строить доказательства и решать математические задачи.

Как связана область математического содержания с другими науками?

Область математического содержания тесно связана с другими науками, такими как физика, химия, биология, экономика и т.д. В этих науках математика используется для моделирования физических и биологических процессов, анализа экономических тенденций и определения финансовых рисков.

Какова роль области математического содержания в повседневной жизни человека?

Область математического содержания имеет широкое применение на практике, в повседневной жизни человека. Например, математика используется в банковском деле при расчете процентных ставок, настройке финансовых моделей, ежедневном учете расходов и доходов.

Какова специфика обучения области математического содержания в школе и вузе?

В школе обучение области математического содержания начинается с простых понятий и определений, постепенно переходя к более сложным темам и задачам. В вузе математика рассматривается глубже и расширяется область ее применения. Обычно вузы предлагают специальности, связанные с математикой и ее применением в науке и технике.

Теория дифференцирования и интегрирования

Дифференцирование — это процесс нахождения производной функции. Производная показывает, как изменится значение функции при изменении ее аргумента. Она играет важную роль в математическом анализе, физике, экономике и других науках.

Существуют различные методы дифференцирования функций, такие как правило дифференцирования произведения, правило дифференцирования сложной функции и др. Каждый из них позволяет вычислить производную функции в зависимости от ее структуры.

Интегрирование — это обратный процесс дифференцированию. Он заключается в нахождении первообразной функции. Первообразная обратна производной функции и позволяет найти значения функции в различных точках.

Существует несколько методов интегрирования, таких как метод замены переменной, метод интегрирования по частям и др. Использование каждого метода зависит от структуры функции и сочетания его элементов.

Теория дифференцирования и интегрирования является одной из основ математического анализа. Она представляет собой мощный инструмент для решения различных задач и нахождения закономерностей в различных областях науки и техники.

Теория алгоритмов и ее приложения

Теория алгоритмов — это раздел математики, изучающий алгоритмы и их свойства. Алгоритм — это последовательность инструкций, которые выполняются для решения определенной задачи. Изучение теории алгоритмов позволяет определить эффективность алгоритма, его сложность и возможность применения в различных областях.

В настоящее время теория алгоритмов находит широкое применение в информационных технологиях. Например, алгоритмы используются в разработке программного обеспечения, баз данных, при обработке изображений и звука, а также в других областях. Теория алгоритмов также является основой для изучения других областей математики, таких как теория вычислимости и компьютерной логики.

Приложения теории алгоритмов находятся в различных областях жизнедеятельности человека. Например, алгоритмы применяются в медицине для анализа медицинских данных и диагностики заболеваний. Они также используются в экономике и финансах для прогнозирования и анализа рынков.

• В компьютерных играх алгоритмы используются для расчета движения игровых персонажей и создания искусственного интеллекта;
• Алгоритмы применяются в транспортных системах для оптимизации маршрутов и расписания;
• В производстве алгоритмы используются для оптимизации линий производства и управления ресурсами;

Таким образом, теория алгоритмов и ее приложения играют важную роль в современном мире, поскольку они способствуют оптимизации и автоматизации различных процессов, а также дают возможность создавать более эффективные и точные модели и системы.