Общее высказывание в математике: определение и примеры

Общее высказывание в математике — это утверждение, которое справедливо для всех объектов некоторого множества. Обычно оно записывается с использованием кванторов все и существует. Понимание общих высказываний важно для понимания математических доказательств и построения новых теорий. Узнайте больше о понятии общих высказываний в математике в данной статье.

Общее высказывание является одним из важных понятий математики, которое используется для выражения отношения между элементами множества. Общее высказывание может быть истинным или ложным, в зависимости от того, выполняется ли оно для всех элементов множества.

Общее высказывание имеет следующую форму: «Для всех x из множества X выполняется свойство P». Где X — множество, а Р — свойство, которое должно выполняться для всех элементов множества.

Пример общего высказывания: «Для всех целых чисел n > 2, существуют простые числа p и q, такие что n = p + q». Это высказывание является истинным, так как оно выполняется для всех целых чисел n > 2.

Общее высказывание также может быть использовано для формулировки теорем и законов математики, что делает его важным инструментом для установления правил и закономерностей в науке.

Что такое общее высказывание в математике?

Общее высказывание в математике — это утверждение, которое описывает свойства, которые есть или отсутствуют у всех элементов некоторого множества.

В математике, общее высказывание формулируется с помощью квантора всеобщности «для всех». Например, выражение «для всех x из множества A выполняется условие P(x)» является общим высказыванием. Оно утверждает, что для любого элемента x из множества A верно условие P(x).

Такие утверждения обычно записываются в виде неформального текста или с использованием символов математической логики. Общие высказывания являются важными в математике и использованы во многих ее областях, таких как теория чисел, геометрия, теория графов и другие.

Примеры общих высказываний:

• Для всех целых чисел n и m, n + m равно m + n.
• Для всех положительных чисел a и b, ab = ba.
• Для всех простых чисел p, p + 2 тоже простое число.

Общие высказывания являются основным инструментом математической логики и являются ключевым элементом доказательств математических утверждений.

Видео по теме:

Примеры общих высказываний в математике

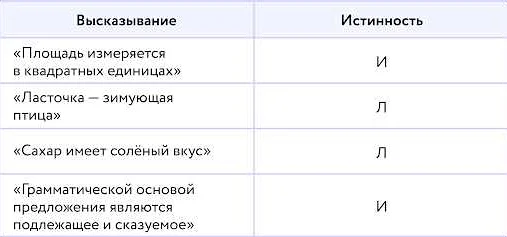
1. Для любых двух целых чисел a и b, их сумма a + b является целым числом.

Это общее высказывание в математике, которое можно записать как «∀ a, b ∈ ℤ, a + b ∈ ℤ». Оно означает, что для любых двух целых чисел сумма этих чисел также будет целым числом.

2. Все углы прямоугольника равны 90 градусов.

Это также общее высказывание, которое можно записать как «∀ ABCD, ∠A = ∠B = ∠C = ∠D = 90°». Оно означает, что для любого прямоугольника углы A, B, C и D будут равны 90 градусов.

3. Для любого вектора u и скаляра a, произведение a·u также является вектором.

Это общее высказывание в линейной алгебре, которое можно записать как «∀ u ∈ V, a ∈ F, a·u ∈ V». Оно означает, что для любого вектора u и любого скаляра a произведение a·u также будет являться вектором.

4. Для любых двух множеств A и B, их пересечение A ∩ B также является множеством.

Это общее высказывание в теории множеств, которое можно записать как «∀ A, B, A ∩ B ⊆ A, B». Оно означает, что для любых двух множеств пересечение этих множеств также будет являться множеством.

5. Все треугольники имеют сумму углов, равную 180 градусов.

Это общее высказывание в геометрии, которое можно записать как «∀ ABC, ∠A + ∠B + ∠C = 180°». Оно означает, что для любого треугольника сумма его углов будет равна 180 градусов.

ПримерВысказывание

1	Для любых двух действительных чисел a и b, a + b = b + a.
2	Для любого многочлена p(x) и константы a, a·p(x) является многочленом.
3	Для любых двух множеств A и B, A ∪ B ⊆ A ∩ B.

6. Для любых двух действительных чисел a и b, существует действительное число c, такое что a + c = b.

Это общее высказывание в алгебре, которое можно записать как «∀ a, b ∈ ℝ, ∃ c ∈ ℝ: a + c = b». Оно означает, что для любых двух действительных чисел a и b существует действительное число c, которое можно прибавить к a, чтобы получить b.

7. Для любого числа x, его квадрат x² неотрицателен.

Это общее высказывание в алгебре, которое можно записать как «∀ x ∈ ℝ, x² ≥ 0». Оно означает, что для любого числа x квадрат этого числа не меньше нуля.

Формы записи общих высказываний

Общее высказывание в математике может быть записано в нескольких формах. Одна из самых распространенных форм — форма кванторов.

Форма кванторов выглядит следующим образом: ∀x P(x), где ∀ обозначает квантор всеобщности, x — переменную, а P(x) — предикат, определяющий свойства переменной. Общее высказывание, записанное в форме кванторов может быть прочитано как «для всех x верно P(x)».

Существует также форма записи существования: ∃x P(x), где ∃ обозначает существование. Общее высказывание в этой форме может быть прочитано как «существует такой x, что P(x) верно».

Вторая популярная форма записи общих высказываний — форма математической индукции. Она используется для доказательства утверждений вида «для всех натуральных чисел n, P(n) верно».

Форма математической индукции включает в себя базовый шаг, заключающийся в доказательстве верности высказывания для n=1, и шаг индукции, где доказывается, что если верно высказывание для n, то оно верно и для n+1.

Иногда общие высказывания записываются в форме таблиц. Таблицы могут быть использованы, когда требуется перечислить все возможные значения переменных и выяснить, в каких случаях высказывание верно.

Важно понимать, что независимо от формы записи, общее высказывание должно быть ясно, точно и однозначно сформулировано. Это позволит избежать неоднозначностей и ошибок в доказательствах и рассуждениях.

Вопрос-ответ:

Что такое общее высказывание в математике?

Общее высказывание в математике — это утверждение, которое справедливо для любого элемента выбранного множества. Например, «все четные числа делятся на 2» — это общее высказывание, потому что оно справедливо для каждого четного числа.

Какие могут быть примеры общих высказываний?

Примеры общих высказываний могут быть различными, например: «здесь нет такого числа, которое будет меньше всех остальных», «любое целое число можно представить в виде суммы трех квадратов», «любые два прямых в пространстве либо пересекаются, либо параллельны».

Как записывают общее высказывание в математике?

Общие высказывания в математике записываются с помощью кванторов всеобщности и существования. Например, «» может означать «для любого элемента множества A, верно высказывание Р».

Какие символы используются в записи общих высказываний?

Для записи общих высказываний в математике используются специальные символы. Для квантора всеобщности используется символ «∀», а для квантора существования — «∃». Например, запись «» означает «для любого элемента множества A, верно высказывание Р», а запись «» — «существует элемент множества A, для которого верно высказывание Р».

Можно ли утверждать, что общее высказывание — это утверждение, верное для всего множества?

Да, общее высказывание — это утверждение, верное для всех элементов выбранного множества.

Какие виды вопросов могут решаться с помощью общих высказываний в математике?

С помощью общих высказываний в математике можно решать различные задачи. Например, можно доказывать теоремы, определять свойства множеств и элементов, решать задачи на экстремум и многое другое.

Что такое квантор всеобщности?

Квантор всеобщности — это математический символ «∀», который используется для записи утверждений, верных для каждого элемента выбранного множества. Например, «» означает, что для любого x из множества A выполняется утверждение P(x).

Кванторы в общих высказываниях

Кванторы являются важной частью общих высказываний в математике. Они используются для указания того, что утверждение справедливо для всех элементов в каком-то множестве (квантор всеобщности) или для некоторых элементов в этом множестве (квантор существования).

Квантор всеобщности обозначается символом ∀ и указывает, что утверждение является истинным для любого элемента в множестве. Например, высказывание «для любого натурального числа n, n + 1 больше n» может быть записано как ∀n ∈ ℕ, n + 1 > n. Здесь символ ∈ обозначает принадлежность элемента множеству.

Квантор существования обозначается символом ∃ и указывает, что утверждение является истинным для некоторого элемента в множестве. Например, высказывание «существует натуральное число, которое является четным» может быть записано как ∃n ∈ ℕ, 2n mod 2 = 0. Здесь символ mod обозначает операцию взятия остатка от деления.

Кванторы могут использоваться в любых общих высказываниях и играют важную роль в математических доказательствах. При использовании кванторов необходимо быть внимательным и точно определять множество, для которого высказывание справедливо, чтобы избежать недостаточности или избыточности утверждения.

Классификация общих высказываний

Общее высказывание — это утверждение, которое может быть верным или ложным в различных обстоятельствах. Общие высказывания играют важную роль в математике и других науках. По форме и содержанию общие высказывания можно классифицировать следующим образом:

1. Утверждение — это общее высказывание, которое может быть либо истинным (верным), либо ложным. Пример: «Сумма двух четных чисел — четное число».
2. Вопрос — это общее высказывание, на которое можно ответить «да» или «нет». Пример: «Является ли 42 простым числом?».
3. Предикат — это общее высказывание, которое содержит переменную, например, «x», и утверждает, что для некоторых значений переменной высказывание верно. Пример: «x^2 > 4» — верно для переменных, которые принимают значения больше 2 или меньше -2.
4. Импликация — это общее высказывание вида «если…то…». Пример: «Если число делится на 6, то оно делится на 2 и на 3».
5. Эквивалентность — это общее высказывание вида «тогда и только тогда, когда». Пример: «Число является квадратом тогда и только тогда, когда оно положительное и имеет нечётную вещественную часть».

Важно понимать, что общие высказывания играют ключевую роль в математике, поэтому важно уметь их формулировать и классифицировать.

Истинность общих высказываний

Общее высказывание — это высказывание, которое справедливо для всех значений из определенной области значений. Например, «все кошки мурчат» и «все собаки лают» — это типичные общие высказывания.

Истинность общих высказываний — это показатель того, является ли общее высказывание истинным для всех значений из данной области значений.

Получить понимание истинности общего высказывания может помочь таблица истинности. В таблице истинности для общего высказывания должны быть представлены все возможные значения переменных, а также результат истинности соответствующей комбинации значений переменных.

Например, для общего высказывания «все кошки мурчат» таблица истинности будет выглядеть следующим образом:

Кошка мурчит?Истинность высказывания

Да	Истина
Нет	Ложь

Таким образом, наша таблица истинности показывает, что общее высказывание «все кошки мурчат» является истинным.

Важно понимать, что истинность общего высказывания может зависеть от области его применения. Например, общее высказывание «все птицы летают» может быть истинным в случае, если мы говорим о всех птицах в мире, но неверным, если мы учитываем птиц, которые не могут летать (например, пингвины).

Ложность общих высказываний

Общее высказывание в математике — это высказывание, которое относится ко всем элементам некоторого множества. Например, высказывание «все треугольники имеют три стороны» является общим, так как оно верно для каждого треугольника.

Однако, не все общие высказывания верны. Например, высказывание «все киты — рыбы» ложно, потому что киты не являются рыбами, хотя это высказывание относится ко всем китам.

Чтобы опровергнуть общее высказывание, достаточно привести один контрпример — элемент множества, для которого высказывание не верно. Например, для опровержения высказывания «все треугольники равнобедренные» достаточно привести треугольник, у которого стороны не равны.

При этом, необходимо понимать, что существуют некоторые общие высказывания, для которых невозможно привести контрпример. Такие высказывания называются общие истинные высказывания. Например, высказывание «все круги имеют одинаковую площадь при одинаковом радиусе» является общим истинным высказыванием, для которого не существует контрпримеров.

Свойства и связи общих высказываний

Противоположное высказывание — это высказывание, которое содержит те же самые элементы, что и данное общее высказывание, но имеет противоположный знак утверждения. Например, если дано общее утверждение «Все кошки любят молоко», то противоположным будет высказывание «Не все кошки любят молоко».

Обратное высказывание — это высказывание, которое получается путем обращения мест утверждения и субъекта в данном общем высказывании. Например, если дано общее утверждение «Все люди — смертны», то обратным будет высказывание «Смертны все люди».

Контрпозиция — это высказывание, в котором и субъект, и утверждение изменены на противоположные и заменены на результат этого изменения. Например, если дано общее утверждение «Если у человека есть деньги, то он счастлив», то контрпозицией будет высказывание «Если у человека нет денег, то он не счастлив».

Конъюнкция двух общих высказываний — это высказывание, в котором оба утверждения соединены словом «и». Например, из общих высказываний «Все кошки любят молоко» и «Все кошки любят рыбу» можно составить конъюнкцию «Все кошки любят молоко и рыбу».

Дизъюнкция двух общих высказываний — это высказывание, в котором оба утверждения соединены словом «или». Например, из общих высказываний «Все люди — смертны» и «Некоторые люди очень богаты» можно составить дизъюнкцию «Люди либо смертны, либо очень богаты».

Применение общих высказываний в математике

Общие высказывания в математике используются для описания свойств и закономерностей, которые характерны для любых объектов из заданной группы. Такие высказывания позволяют сформулировать общие законы, которые могут быть применены к неограниченному количеству объектов.

Например, общее высказывание «любое четное число делится на 2» описывает свойство четных чисел, которое является характерным для всех четных чисел. Такое высказывание позволяет нам сформулировать закон, который будет работать для любого четного числа, а не только для какого-то конкретного числа.

Общие высказывания также широко используются в математических доказательствах. Например, при доказательстве теоремы о среднем значении для функций одной переменной используется общее высказывание о существовании корня на отрезке, которое применяется не только к конкретной функции, но и к любой другой функции, удовлетворяющей определенным условиям.

Также общие высказывания часто используются для формулировки алгоритмов и абстрактных понятий в математике. Например, общее высказывание «любое конечное множество можно упорядочить» позволяет нам сформулировать алгоритм сортировки, который может быть применен для любого конечного множества.

В целом, общие высказывания играют важную роль в математике, позволяя описывать закономерности, которые применимы к неограниченному количеству объектов, и формулировать законы, которые работают для целых классов математических объектов.

Общие высказывания в решении математических задач

При решении математических задач полезно использовать общие высказывания, которые помогают упростить и систематизировать решение. Они могут быть использованы в различных областях математики, включая алгебру, геометрию, тригонометрию и т.д.

Одним из важных общих высказываний является принцип математической индукции. Он используется для доказательства утверждений о целых числах, основываясь на их структуре и свойствах. Согласно принципу, если утверждение верно для некоторого числа (например, для 1), и верно для следующего числа после этого (например, для n+1, где n — любое целое число), то оно верно для всех целых чисел.

Другим важным общим высказыванием является принцип Дирихле, который используется при решении задач в комбинаторике. Принцип гласит, что если n+1 объектов размещены в n контейнерах, то как минимум один контейнер содержит более одного объекта. Это высказывание может быть полезно, например, при решении задач на выбор комитета из группы людей.

Еще одним общим высказыванием является принцип Куни-Такера, который используется в логике и математическом анализе. Он заключается в том, что любое утверждение может быть выражено как конъюнкция (логическое «и») исключительных случаев, или дизъюнкция (логическое «или») обычных случаев. Это позволяет упростить формулировки утверждений и выводов.

Все эти общие высказывания помогают систематизировать и упростить решение математических задач, позволяя понять, какие пути решения следует изучать и где следует искать ответы.

Общие высказывания в математических доказательствах

В математических доказательствах общее высказывание – это утверждение, которое верно для любых значений переменных. Обычно оно записывается в виде универсального квантора ∀ (читается «для любого») и переменной, которая принимает значения из некоторого множества. Например, ∀x ∈ N (x + 1 > x).

Общие высказывания в математических доказательствах играют важную роль, так как они позволяют сделать выводы о свойствах объектов, не имея точной информации об отдельных элементах множества.

К примеру, при решении задачи на нахожение суммы ряда можно использовать общее высказывание о свойствах сходящихся рядов: «Если ряд сходится, то его члены стремятся к нулю». Это утверждение помогает установить, что сумму ряда можно вычислить, даже если мы не знаем значения его отдельных членов.

Общим высказыванием может быть также некоторое равенство, например, ∀x ∈ R (x^2 ≥ 0). Оно верно для любого вещественного числа x и позволяет делать выводы об алгебраических операциях с квадратами чисел.

Кроме того, общее высказывание может содержать отрицание (символ ¬, читается «не»). Например, ∀x ∈ R ¬(x > x^2). Такое высказывание означает, что любое вещественное число меньше или равно своему квадрату.

В заключение, общее высказывание в математических доказательствах является важным инструментом для получения более общих выводов из ограниченных условий. Оно позволяет сделать выводы, которые верны для всей выборки, а не только для отдельных элементов множества.