Что является высказыванием в математической логике

Высказывание в математической логике — это утверждение, которое может быть истинным или ложным. В данной статье мы рассмотрим основные принципы формулирования и оценки высказываний в математической логике, а также приведем примеры и объяснения для лучшего понимания концепции высказывания.

Высказывание в математической логике — это утверждение, которое может быть либо истинным, либо ложным. Оно является основным понятием в логике и образует основу для рассмотрения и анализа различных утверждений и рассуждений.

Высказывание может быть представлено в виде предложения, состоящего из слов и символов, которые имеют строго определенное значение. Например, высказывание «2 + 2 = 4» является истинным, в то время как высказывание «2 + 2 = 5» является ложным.

Высказывание может быть простым или сложным. Простое высказывание представляет собой утверждение, которое не может быть разделено на более мелкие составляющие. Например, высказывания «Солнце светит» и «Дождь идет» являются простыми.

Сложное высказывание состоит из нескольких простых высказываний, объединенных логическими связками. Например, высказывание «Если сегодня солнечно, то я пойду гулять» состоит из двух простых высказываний, связанных логической связкой «если…то».

Высказывание в математической логике: основные понятия и примеры

Высказывание может быть представлено как простое, то есть состоять из одной части, или составным, когда оно состоит из нескольких частей, объединенных логическими связками.

Основные логические связки, которые используются для формирования составных высказываний, включают:

• Конъюнкцию (логическое «и»)
• Дизъюнкцию (логическое «или»)
• Импликацию (логическое «если…то…»)
• Отрицание (логическое «не»)

Примеры простых высказываний:

1. «2 + 2 = 4»
2. «Солнце восходит на востоке»
3. «Этот треугольник является прямоугольным»

Примеры составных высказываний:

1. «Сегодня будет солнечно и тепло»
2. «Если я поеду в отпуск, то куплю новый купальник»
3. «Либо пойду в кино, либо останусь дома и посмотрю фильм»

Математическая логика позволяет анализировать, выводить и доказывать различные свойства высказываний, что является важным инструментом в решении математических задач и построении доказательств.

Определение высказывания

Высказывания могут быть простыми или составными. Простые высказывания — это высказывания, которые не могут быть разбиты на более мелкие составляющие. Например, «2 + 2 = 4» и «Солнце восходит на востоке» являются простыми высказываниями.

Составные высказывания состоят из нескольких простых высказываний, объединенных логическими операторами. Логические операторы могут быть использованы для объединения, инверсии или комбинирования высказываний. Примеры составных высказываний: «Если сегодня идет дождь, то я возьму зонтик» и «Либо утро, либо вечер».

ВысказываниеИстинно (True)Ложно (False)

2 + 2 = 4	Да	Нет
Солнце восходит на востоке	Да	Нет
Если сегодня идет дождь, то я возьму зонтик	Зависит от погоды	Зависит от погоды
Либо утро, либо вечер	Да	Нет

Логические операторы

Логические операторы используются в математической логике для комбинирования простых высказываний и создания сложных высказываний. Они позволяют нам строить логические цепочки и проводить рассуждения на основе этих цепочек.

Основными логическими операторами являются:

• Конъюнкция (логическое И): обозначается символом ∧ (или просто через запятую) и возвращает истинное значение только в том случае, когда оба операнда истинны. Например, высказывание «2 > 1 ∧ 3 > 2» будет истинным, так как оба условия выполняются.
• Дизъюнкция (логическое ИЛИ): обозначается символом ∨ и возвращает истинное значение, если хотя бы один из операндов истинный. Например, высказывание «2 > 3 ∨ 3 > 2» будет истинным, так как хотя бы одно из условий выполняется.
• Отрицание: обозначается символом ¬ и меняет значения высказывания на противоположное. Например, высказывание «¬(2 > 3)» будет истинным, так как условие «2 > 3» ложно.
• Импликация: обозначается символом → и возвращает истинное значение, если первый операнд ложный или если оба операнда истинные. Например, высказывание «2 > 3 → 3 > 2» будет ложным, так как первое условие «2 > 3» не выполняется.
• Эквиваленция: обозначается символом ↔ и возвращает истинное значение, если оба операнда имеют одинаковое значение и ложное значение, если они отличаются. Например, высказывание «2 > 3 ↔ 3 > 2» будет ложным, так как условия не имеют одинакового значения.

Логические операторы позволяют нам строить сложные высказывания и проводить рассуждения на основе этих высказываний. Они являются важным инструментом в математической логике и науке в целом.

Истинность и ложность высказывания

В математической логике высказывание может быть либо истинным, либо ложным. Истинность или ложность высказывания зависит от значения его компонентов.

Высказывания в математической логике состоят из пропозициональных переменных и логических связок. Пропозициональные переменные могут принимать значения истины или лжи. Логические связки определяют отношения между пропозициональными переменными и позволяют выражать различные логические операции.

Истинность или ложность высказывания можно определить с помощью таблицы истинности. В таблице истинности перечисляются все возможные комбинации значений пропозициональных переменных, а затем указывается результат выражения в каждом случае.

Например, высказывание «если $p$ истинно, то $q$ истинно» может быть представлено в виде таблицы истинности:

$p$$q$Высказывание

Истина	Истина	Истина
Истина	Ложь	Ложь
Ложь	Истина	Истина
Ложь	Ложь	Истина

Из таблицы истинности видно, что высказывание является истинным только в двух случаях: если $p$ и $q$ оба истинны или если $p$ ложно и $q$ истинно. В остальных случаях высказывание ложно.

Таким образом, в математической логике истинность и ложность высказывания определяются на основе значений его компонентов и логических связок, которые между ними устанавливаются.

Примеры простых высказываний

Ниже приведены примеры простых высказываний:

1. 2 + 2 = 4

Это высказывание утверждает, что сумма двух и двух равна четырем. Оно истинно, так как это математический факт.

2. Луна круглая

Это высказывание утверждает, что форма Луны является круглой. Оно ложно, так как Луна имеет несколько выпуклостей и впадин.

3. 5 > 10

Это высказывание утверждает, что пять больше десяти. Оно ложно, так как пять меньше десяти.

4. Москва — столица России

Это высказывание утверждает, что Москва является столицей России. Оно истинно, так как Москва действительно является столицей Российской Федерации.

5. Вода кипит при 100 градусах Цельсия

Это высказывание утверждает, что вода начинает кипеть при температуре 100 градусов Цельсия. Оно истинно, так как это физический факт.

Это лишь несколько примеров простых высказываний, которые могут быть использованы в математической логике. Они являются основой для более сложных логических конструкций.

Составные высказывания

В математической логике существуют высказывания, которые можно разделить на простые и составные. Составные высказывания состоят из двух или более простых высказываний, которые связаны логическими операторами.

Логические операторы используются для комбинирования простых высказываний и образования новых составных высказываний. Наиболее распространенными логическими операторами являются:

• Конъюнкция (и): обозначается символом ∧ или ∩. Высказывание «p и q» истинно только в том случае, если и высказывание p, и высказывание q истинны.
• Дизъюнкция (или): обозначается символом ∨ или V. Высказывание «p или q» истинно, если хотя бы одно из высказываний p и q истинно.
• Импликация (если…то): обозначается символом →. Высказывание «если p, то q» истинно, если p ложно или q истинно.
• Эквиваленция (тогда и только тогда, когда): обозначается символом ↔. Высказывание «p тогда и только тогда, когда q» истинно, если p и q имеют одинаковое значение истинности.
• Отрицание (не): обозначается символом ¬ или ~. Высказывание «не p» истинно, если высказывание p ложно.

Примеры составных высказываний:

• Высказывание p: «Солнце светит». Высказывание q: «Дождь идет». Высказывание «p и q» обозначает «Солнце светит и дождь идет».
• Высказывание p: «2+2=4». Высказывание q: «3+3=6». Высказывание «p или q» обозначает «2+2=4 или 3+3=6».
• Высказывание p: «Если сегодня пятница, то завтра суббота». Высказывание q: «Сегодня пятница». Высказывание «если p, то q» обозначает «Если сегодня пятница, то завтра суббота».

Таким образом, составные высказывания позволяют строить более сложные логические конструкции, которые помогают анализировать и описывать различные ситуации и отношения в математике и других науках.

Примеры составных высказываний

ВысказываниеФормула

Математика интересна и полезна	p & q
Солнце светит или идет дождь	p | q
Это не правда	¬p
Если я прочитаю эту книгу, то получу знания	p → q

В первом примере используется связка «и» (логическое умножение). Если оба простых высказывания (Математика интересна и Математика полезна) истинны, то и составное высказывание будет истинным.

Во втором примере используется связка «или» (логическое сложение). Если хотя бы одно из простых высказываний (Солнце светит или идет дождь) истинно, то и составное высказывание будет истинным.

В третьем примере используется отрицание. Простое высказывание «Это правда» отрицается и становится «Это не правда».

В четвертом примере используется связка «если…то». Если простое высказывание «Я прочитаю эту книгу» истинно, то и следующее простое высказывание «Я получу знания» будет истинно.

Логические связки

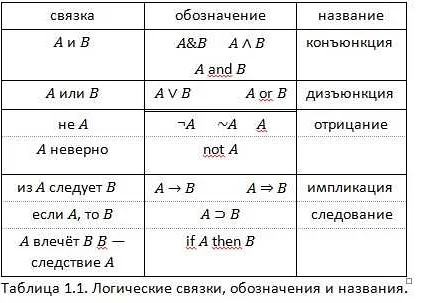
В математической логике логические связки используются для объединения или преобразования простых высказываний. Они позволяют строить сложные высказывания на основе уже существующих.

Существует несколько основных логических связок:

• И (конъюнкция): высказывание A и высказывание B истинны только если оба высказывания истинны. Например, «2 < 3 и 4 > 1″ — истина.
• Или (дизъюнкция): высказывание A или высказывание B истинно если хотя бы одно из них истинно. Например, «2 < 3 или 4 > 5″ — истина.
• НЕ (отрицание): высказывание не A истинно если A ложно. Например, «не(2 > 3)» — истина.
• Импликация: высказывание A имплицирует высказывание B, если из истинности A следует истинность B. Например, «если 2 > 3, то 4 < 5» — истина.
• Эквивалентность: высказывание A эквивалентно высказыванию B, если они имеют одинаковую истинностную таблицу. Например, «2 + 2 = 4 эквивалентно 3 + 1 = 5″ — истина.

Использование логических связок позволяет строить более сложные и точные математические высказывания, которые могут быть использованы для доказательства или решения различных задач.

Примеры использования логических связок

Логические связки широко применяются в математической логике для формирования и анализа высказываний. Рассмотрим несколько примеров использования логических связок:

ПримерВысказывание

1	Если сегодня идет дождь, то улица мокрая.
2	Либо солнце светит, либо облачно.
3	Если число делится на 2 и 3 одновременно, то оно делится на 6.
4	Если треугольник равносторонний, то он также является равноугольным.

В каждом из этих примеров логические связки позволяют выразить отношения между различными высказываниями и сделать выводы на основе логических законов.

Видео по теме:

Что такое высказывание в математической логике?

Высказывание в математической логике — это утверждение, которое может быть либо истинным, либо ложным. Оно должно быть составлено таким образом, чтобы иметь определенное значение и быть однозначно истинным или ложным. Например, «2 + 2 = 4» или «Все собаки имеют хвост» — это высказывания, так как они имеют определенное значение и могут быть проверены на истинность или ложность.

Какие основные свойства имеют высказывания в математической логике?

В математической логике высказывания имеют два основных свойства: истинность и ложность. Высказывание может быть истинным, если его значение соответствует действительности или правде. Например, высказывание «2 + 2 = 4» является истинным. Высказывание также может быть ложным, если его значение не соответствует действительности или правде. Например, высказывание «2 + 2 = 5» является ложным.

Что такое высказывание в математической логике?

Высказывание в математической логике — это утверждение, которое может быть либо истинным, либо ложным.