Что такое ограничение в математике
Содержимое
- 1 Что такое ограничение в математике
- 1.1 Что такое ограничение в математике
- 1.2 Видео по теме:
- 1.3 Примеры ограничений в математике
- 1.4 Основные понятия ограничений
- 1.5 Свойства ограничений в математике
- 1.6 Зачем нужны ограничения в математике
- 1.7 Ограничения в различных областях математики
- 1.8 Интересные факты о ограничениях в математике
- 1.9 Вопрос-ответ:
- 1.9.0.1 Что такое ограничение в математике?
- 1.9.0.2 Как определить ограничение функции?
- 1.9.0.3 Какие примеры ограничений существуют в математике?
- 1.9.0.4 Чем отличается одностороннее ограничение от двустороннего?
- 1.9.0.5 Какие понятия связаны с ограничением в математике?
- 1.9.0.6 Что такое ограничение в математике?
- 1.9.0.7 Как определить ограничение функции?
Ограничение в математике — это значение, к которому стремится функция или последовательность при приближении аргумента к определенной точке или бесконечности. Ограничение позволяет определить поведение функции или последовательности в окрестности данной точки и играет важную роль в анализе и решении математических задач.
Ограничение, являющееся одним из важных понятий в математике, определяет поведение функции вблизи определенной точки или при стремлении аргумента к некоторому значению. В основе этого понятия лежит идея того, что функция может принимать определенное значение, когда ее аргумент находится достаточно близко к определенной точке.
Для того чтобы лучше понять ограничение функции, рассмотрим пример. Предположим, у нас есть функция f(x) = x^2. Если мы рассмотрим поведение этой функции вблизи точки x = 2, то можем заметить, что при стремлении x к 2, значения функции становятся все ближе к 4. Это означает, что 4 является ограничением функции f(x) при x, стремящемся к 2.
Ограничения функций могут быть как числовыми, так и символическими. Например, в функции f(x) = 1/x, ограничение при x, стремящемся к бесконечности, равно нулю. Это можно выразить следующим образом: при x, стремящемся к бесконечности, f(x) стремится к 0. Ограничения также могут быть положительными, отрицательными или равными нулю, в зависимости от поведения функции вблизи определенной точки или при стремлении аргумента к некоторому значению.
Ограничение функций играет важную роль в математическом анализе и различных областях приложений. Оно позволяет определить поведение функции вблизи определенной точки или в пределе и является основным инструментом для изучения функций и их свойств.
Что такое ограничение в математике

Формально, ограничение функции f(x) при x, стремящемся к a, обозначается как:
lim(x->a) f(x)
Где a — точка, к которой стремится аргумент x. Если значение функции f(x) приближается к определенному числу L при приближении x к a, то говорят, что ограничение функции f(x) равно L:
lim(x->a) f(x) = L
Ограничение функции может быть равно бесконечности или не существовать вовсе. В таких случаях используются специальные обозначения:
lim(x->a) f(x) = ∞ — ограничение равно бесконечности
lim(x->a) f(x) = -∞ — ограничение равно минус бесконечности
lim(x->a) f(x) не существует — ограничение не существует
Ограничение в математике позволяет решать различные задачи, такие как нахождение пределов функций, определение асимптот, анализ поведения функций в окрестности определенных точек и т. д. Это важное понятие для понимания и изучения функций и их свойств.
Видео по теме:
Примеры ограничений в математике
Ниже приведены некоторые примеры ограничений в математике:
- Ограничение на диапазон значений переменной: например, переменная может принимать только положительные значения или быть ограничена сверху или снизу.
- Ограничение на область определения функции: функция может быть определена только для определенных значений аргумента.
- Ограничение на связь между переменными: например, сумма двух переменных может быть ограничена определенным числом или некоторая переменная может быть пропорциональна другой.
- Ограничение на точность решения: при решении математической задачи может быть задана определенная погрешность, которую нужно учесть.
- Ограничение на время выполнения: в некоторых задачах может требоваться решение в определенные сроки или установлено ограничение на время, которое можно потратить на выполнение решения.
Ограничения в математике играют важную роль при решении задач и позволяют определить допустимые решения. Важно учитывать ограничения при проведении вычислений и анализе математических моделей.
Основные понятия ограничений
Существуют два основных типа ограничений: односторонние и двусторонние. Одностороннее ограничение указывает, с какой стороны функция стремится к определенному значению. Например, если функция f(x) стремится к L при x->a справа, это можно записать как f(x)->L при x->a+.
Двустороннее ограничение указывает, что функция стремится к определенному значению как справа, так и слева. Функция f(x) стремится к L при x->a, если f(x)->L при x->a+ и f(x)->L при x->a-.
Ограничения также могут быть бесконечными. Если функция стремится к бесконечности при приближении к определенной точке, это можно записать как f(x)->∞ при x->a. Аналогично, если функция стремится к минус бесконечности, это можно записать как f(x)->-∞ при x->a.
Важным понятием, связанным с ограничениями, является понятие предела функции. Предел функции описывает поведение функции в окрестности определенной точки и позволяет определить ее ограничения. Предел функции может быть равен конечному числу или бесконечности в зависимости от поведения функции в окрестности точки.
Ограничения играют важную роль в различных областях математики, физики и других наук. Они позволяют анализировать функции и моделировать поведение систем в различных условиях. Понимание основных понятий ограничений является важным шагом в изучении математики и ее применения в других областях.
Свойства ограничений в математике

Ограничения могут иметь различные свойства, которые определяют их характеристики и влияют на решение математических задач. Некоторые из основных свойств ограничений в математике:
СвойствоОписание
| Линейность | Ограничение может быть линейным, если оно задается линейным уравнением или неравенством. Линейные ограничения часто встречаются в задачах оптимизации и линейном программировании. |
| Нелинейность | Ограничение может быть нелинейным, если оно задается нелинейным уравнением или неравенством. Нелинейные ограничения более сложны в решении, но позволяют моделировать более сложные математические проблемы. |
| Односторонность | Ограничение может быть односторонним, если оно определяет только верхнюю или только нижнюю границу для переменной. Односторонние ограничения часто возникают в задачах оптимизации и ограниченных ресурсах. |
| Двусторонность | Ограничение может быть двусторонним, если оно определяет как верхнюю, так и нижнюю границу для переменной. Двусторонние ограничения часто встречаются в задачах равновесия и симметрии. |
Свойства ограничений позволяют более точно формулировать задачи и ограничивать область поиска решений. Использование правильных свойств ограничений помогает упростить и эффективно решить математические проблемы в различных областях науки и техники.
Зачем нужны ограничения в математике

Ограничения применяются в математике по нескольким причинам:
| 1. | Ограничения позволяют изучать и анализировать конкретные случаи и ситуации, которые могут возникнуть в реальном мире или в других науках. Например, ограничения могут быть полезными при решении задач, связанных с физикой, экономикой или биологией. |
| 2. | Ограничения помогают упрощать и структурировать математические модели и теории. Они позволяют установить определенные условия, при которых исследуемые объекты и свойства могут быть более точно изучены и описаны. Это может значительно облегчить решение задач и проведение математических исследований. |
| 3. | Ограничения могут помочь избежать некорректных или неправильных выводов. Они позволяют исключить некоторые случаи или значения, которые могут ввести в заблуждение или привести к некорректным результатам. В этом смысле ограничения служат фильтрами, которые позволяют выбрать только те решения и результаты, которые удовлетворяют определенным условиям и требованиям. |
Таким образом, ограничения в математике играют важную роль в ее развитии и применении. Они позволяют определить исследуемые предметы и понятия, установить условия и рамки для их изучения, а также помогают упростить и структурировать математические модели и теории.
Ограничения в различных областях математики
- Алгебра: В алгебре ограничения могут быть связаны с диапазонами значений переменных. Например, уравнение x^2 — 4 = 0 имеет ограничение x ≠ 2, так как в этом случае деление на ноль неопределено.
- Геометрия: В геометрии ограничения могут быть связаны с границами фигур или условиями построения. Например, треугольник суммы сторон которого равны 10 метров имеет ограничение на длину каждой из сторон, например a ≤ 5, b ≤ 5, c ≤ 5.
- Теория вероятностей: В теории вероятностей ограничения могут быть связаны с вероятностью событий. Например, вероятность события A должна быть ограничена от 0 до 1, то есть 0 ≤ P(A) ≤ 1.
- Дифференциальное исчисление: В дифференциальном исчислении ограничения могут быть связаны с допустимыми значениями производной функции. Например, функция f(x) = √x имеет ограничение x ≥ 0, так как корень из отрицательного числа неопределен.
Ограничения играют важную роль в математике, позволяя определить допустимые значения переменных или функций в различных областях. Понимание ограничений позволяет более точно анализировать и решать математические задачи.
Интересные факты о ограничениях в математике

Ограничения в математике играют важную роль и применяются во многих областях. Вот несколько интересных фактов о ограничениях:
1. Ограничение может быть как числовым, так и функциональным. Числовое ограничение ограничивает значение переменной, например, x < 5. Функциональное ограничение ограничивает поведение функции, например, f(x) > 0.
2. Ограничение может быть явным или неявным. Явное ограничение задается явно в виде уравнения или неравенства, например, x < 5. Неявное ограничение задается неявно, через связь между переменными или функциями.
3. Ограничение может быть строгим или нестрогим. Строгое ограничение требует точного соответствия условию, например, x > 5. Нестрогое ограничение позволяет некоторое отклонение от условия, например, x ≥ 5.
4. Ограничения используются для определения диапазонов значений переменных или поведения функций. Они помогают установить границы и ограничения для решения математических задач и оптимизации процессов.
5. Ограничения широко применяются в оптимизационных задачах, где требуется найти наилучшее решение с учетом заданных ограничений. Они помогают ограничить пространство поиска и сделать задачу более эффективной.
6. Ограничения могут быть линейными или нелинейными. Линейные ограничения задаются линейными уравнениями или неравенствами, например, ax + by < c. Нелинейные ограничения задаются нелинейными уравнениями или неравенствами, например, x^2 + y^2 < r^2.
7. Ограничения могут быть статическими или динамическими. Статические ограничения остаются постоянными во время всего процесса решения задачи. Динамические ограничения могут изменяться в зависимости от условий или других переменных.
Таким образом, ограничения являются важным инструментом в математике и играют ключевую роль в решении различных задач. Понимание и использование ограничений помогает установить границы и ограничения для достижения оптимального результата.
Вопрос-ответ:
Что такое ограничение в математике?
Ограничение в математике – это понятие, которое используется для определения поведения функции при стремлении аргумента к определенному значению. Оно позволяет выяснить, чему равняется функция в пределе, когда аргумент стремится к определенному значению.
Как определить ограничение функции?
Чтобы определить ограничение функции, нужно проанализировать ее поведение при стремлении аргумента к определенному значению. Если функция приближается к конкретному числу при всех достаточно близких значениях аргумента, то это число и будет ограничением функции.
Какие примеры ограничений существуют в математике?
Примеры ограничений в математике включают: ограничения функций, ограничения последовательностей и ограничения числовых множеств. Например, функция f(x) = 1/x имеет ограничение 0 при x стремящемся к бесконечности. Последовательность 1/n имеет ограничение 0 при n стремящемся к бесконечности. Числовое множество [0, 1] имеет ограничение 1, так как все его элементы не превышают 1.
Чем отличается одностороннее ограничение от двустороннего?
Одностороннее ограничение определяет поведение функции при приближении аргумента с одной стороны. Например, одностороннее ограничение функции f(x) = √x при x, стремящемся к 4 справа, равно 2, так как f(x) при x > 4 приближается к 2. Двустороннее ограничение определяет поведение функции при приближении аргумента с обеих сторон. Например, двустороннее ограничение функции f(x) = 1/x при x, стремящемся к бесконечности, равно 0, так как f(x) при x > 0 приближается к 0, а при x < 0 приближается к 0.
Какие понятия связаны с ограничением в математике?
С ограничением в математике связаны такие понятия, как предел функции, асимптота функции, непрерывность функции и производная функции. Предел функции определяет ограничение функции при стремлении аргумента к определенному значению. Асимптота функции – это линия, к которой функция приближается при стремлении аргумента к бесконечности. Непрерывная функция не имеет рывков и разрывов. Производная функции показывает ее скорость изменения.
Что такое ограничение в математике?
Ограничение в математике — это понятие, которое описывает поведение функции вблизи определенной точки. Когда говорят о пределе функции, то рассматривают ее значения приближающиеся к определенной точке, но не достигающие ее. Ограничение может быть как конечным, так и бесконечным.
Как определить ограничение функции?
Чтобы определить ограничение функции, нужно исследовать ее поведение при приближении аргумента к определенной точке. Если значения функции стремятся к конечному числу при достаточно малых значениях аргумента, то говорят, что функция имеет конечное ограничение. Если значения функции стремятся к бесконечности, то говорят, что функция имеет бесконечное ограничение.

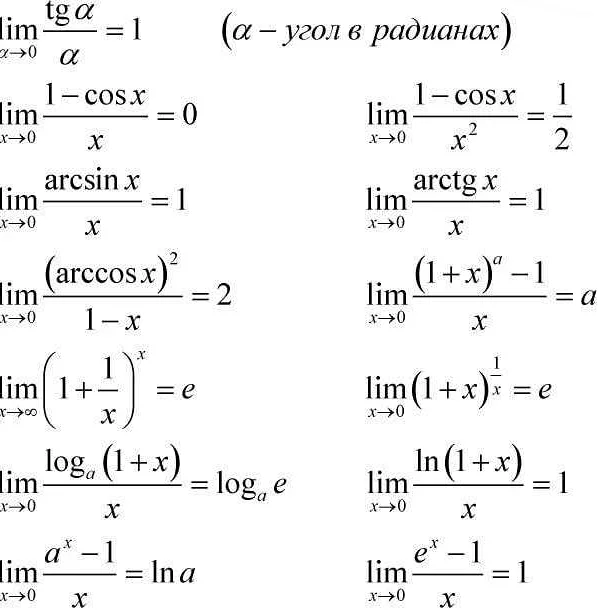



Статья очень понятно и доступно объясняет понятие ограничения в математике. Мне нравится, что автор приводит примеры из реальной жизни, чтобы проиллюстрировать концепцию. Ограничение — это важное понятие, которое помогает нам определить диапазон значений переменных или функций. Это позволяет нам решать задачи и находить оптимальные решения. Я также узнала о разных типах ограничений, таких как ограничения на переменные, ограничения на функции и ограничения на системы уравнений. В целом, статья очень информативная и полезная для тех, кто хочет узнать больше о математических ограничениях. Большое спасибо автору!
Отличная статья! Ограничения в математике – это такая интересная и важная тема. Благодаря ограничениям, мы можем определить предел функции или решить сложные математические задачи. Примеры семей образовательных ограничений оказались очень полезными. Ограничение – это условие, которое можно наложить на переменную или функцию, чтобы ограничить ее диапазон значений. Что касается пределов функций, я всегда задаюсь вопросом – как функция будет вести себя, когда аргумент стремится к бесконечности? И теперь я понимаю, что предельное значение – это то, к чему стремится функция в таком случае. Большое спасибо за прояснение этой темы!
Всегда интересно расширять свой кругозор и узнавать что-то новое. Статья ограничении в математике оказалась для меня настоящим открытием. Оказывается, ограничение — это такое понятие, которое помогает нам определить границы функций и последовательностей. Например, ограничение функции может быть полезно в определении ее предела или максимального значения. Прочитав эту статью, я поняла, что такие понятия, как предел функции, бесконечно малое и бесконечно большое, тесно связаны с ограничениями. Это дало мне более полное представление о математических концепциях и их взаимосвязи. Спасибо автору за такую подробную и понятную статью! Чувствую, что теперь мое понимание математики стало гораздо глубже.