Что такое отрезок 5 класс математика определение

Отрезок в математике — это часть прямой между двумя точками. В данной статье рассмотрено определение отрезка в 5 классе математики и его свойства.

В математике отрезок является одним из основных понятий, которое изучается уже в начальной школе. Отрезок – это часть прямой, которая заключена между двумя точками. Два конца отрезка называются его концами. Отрезок обозначается двумя точками, между которыми он находится, например, AB. Концы отрезка также могут обозначаться буквами A и B. Важно понимать, что точки A и B принадлежат отрезку AB, а все остальные точки прямой, на которой лежит отрезок, не принадлежат ему.

Отрезки могут быть разной длины. Длина отрезка – это расстояние между его концами. Для измерения длины отрезка используется специальная единица измерения – метр. Но в школьной программе обычно используются условные единицы измерения, такие как сантиметры или миллиметры. Важно уметь измерять длину отрезка с помощью линейки или другого измерительного инструмента.

Примеры:

Рассмотрим примеры отрезков. Пусть AB – отрезок, который представляет собой часть прямой между точками А и В. Если мы возьмем линейку и измерим этот отрезок, то узнаем его длину. Например, пусть длина отрезка AB равна 5 сантиметров. Тогда мы можем записать это в виде AB = 5 см. Это означает, что отрезок AB имеет длину 5 сантиметров.

Другой пример – отрезок CD. Пусть его длина равна 8 миллиметров. Тогда это можно записать как CD = 8 мм. Таким образом, отрезок CD имеет длину 8 миллиметров.

Отрезки могут быть разной длины и иметь разные названия. Они могут быть как очень короткими, так и очень длинными. Знание понятия отрезка и умение измерять его длину являются важными навыками в математике и в повседневной жизни.

Что такое отрезок в математике

Отрезок имеет определенную длину, которая измеряется в единицах длины, таких как сантиметры или метры. Длина отрезка определяется разностью координат его концов. Например, если координаты точки A равны (2, 3), а координаты точки B равны (6, 7), то длина отрезка AB равна 6 — 2 = 4 и 7 — 3 = 4. Таким образом, длина отрезка AB равна 4 единицам длины.

Отрезки можно сравнивать по длине. Если отрезок AB длиннее отрезка CD, то можно записать AB > CD. Если отрезки имеют одинаковую длину, то можно записать AB = CD. Если отрезок AB короче отрезка CD, то можно записать AB < CD.

Отрезки могут быть открытыми или закрытыми. Открытый отрезок не включает свои концы и обозначается соответствующими скобками, например (AB). Закрытый отрезок включает свои концы и обозначается соответствующими квадратными скобками, например [AB].

Отрезки в математике играют важную роль при изучении геометрии и алгебры. Они используются для измерения расстояний, построения геометрических фигур и решения уравнений.

ПримерОписание

AB	Отрезок между точками A и B
BC	Отрезок между точками B и C
CD	Отрезок между точками C и D

Как определить отрезок на числовой прямой

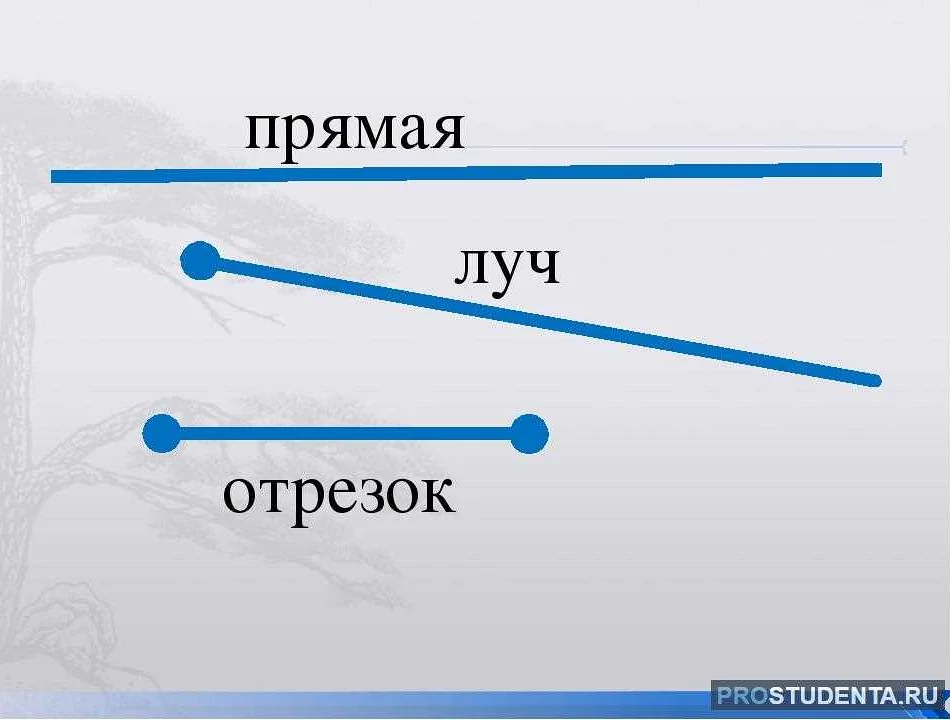
Начальная точка отрезка обозначается левой стрелкой, а конечная точка — правой стрелкой. На числовой прямой отрезок обозначается через две точки, между которыми ставится знак «минус». Например, отрезок между точками -3 и 5 будет обозначаться как [-3, 5].

Чтобы найти длину отрезка, нужно вычислить разность между его конечной и начальной точкой. В нашем примере, длина отрезка [-3, 5] равна 5 — (-3) = 8.

Отрезки могут быть как положительными, так и отрицательными, в зависимости от значений их начальной и конечной точек. Например, отрезок [0, 4] — положительный, а отрезок [-6, -2] — отрицательный.

Также отрезки могут быть равны нулю, если их начальная и конечная точки совпадают. Например, отрезок [2, 2] равен нулю.

Определение и работа с отрезками на числовой прямой важны при изучении различных математических понятий и задач, например, при решении уравнений и неравенств, а также при изучении геометрии.

Символическое обозначение отрезка

В математике отрезок обозначается специальным символом, который состоит из двух точек, расположенных на концах отрезка, и выглядит как вертикальная черта. Например, отрезок, соединяющий точки A и B, обозначается символом AB.

Также можно использовать символическое обозначение для отрезков, которые содержат более двух точек. Например, если отрезок соединяет точки A, B, C и D, его можно обозначить символом ABCD.

Символическое обозначение отрезка позволяет удобно записывать его в математических формулах и уравнениях. Например, если нужно записать уравнение, описывающее отрезок AB, можно использовать следующую форму: AB = {P | P находится на отрезке AB}.

СимволОбозначение

AB	Отрезок, соединяющий точки A и B
ABCD	Отрезок, соединяющий точки A, B, C и D

Примеры отрезков на числовой прямой

Пример 1: Рассмотрим отрезок, который содержит все целые числа от -3 до 3. Он может быть обозначен как [-3, 3].

Пример 2: Пусть отрезок содержит все числа от -2 до 5, не включая -2 и 5. Такой отрезок может быть обозначен как (-2, 5).

Пример 3: Рассмотрим отрезок, который содержит только число 0. Такой отрезок обозначается как {0}.

Пример 4: Отрезок, который не содержит ни одного числа, называется пустым отрезком и обозначается пустым множеством ∅.

Отрезки на числовой прямой используются для представления интервалов, диапазонов и других математических концепций.

Отрезки с целыми числами

Если говорить об отрезках с целыми числами, то это отрезки, на которых находятся только целые числа. Например, отрезок [2, 6] — это отрезок, который начинается с числа 2 и заканчивается числом 6, причем на этом отрезке находятся все целые числа от 2 до 6 включительно: 2, 3, 4, 5, 6.

Отрезки с целыми числами могут быть как положительными, так и отрицательными. Например, отрезок [-3, 2] — это отрезок, который начинается с числа -3 и заканчивается числом 2, причем на этом отрезке находятся все целые числа от -3 до 2 включительно: -3, -2, -1, 0, 1, 2.

Отрезки с целыми числами могут быть использованы в различных задачах, например, при решении уравнений или построении графиков функций. Они позволяют ограничить область значений переменной и упростить решение задачи.

Отрезки с дробными числами

Отрезок с дробными числами представляет собой участок прямой, где начало и конец отрезка могут быть дробными числами. Для определения отрезка с дробными числами, необходимо указать начало и конец отрезка в виде десятичных дробей или дробей.

Например, отрезок [1.5, 3.2] представляет собой участок прямой, который начинается с числа 1.5 и заканчивается числом 3.2. Все числа, находящиеся между этими двумя числами, также принадлежат данному отрезку. Такой отрезок можно представить графически на числовой прямой.

Отрезки с дробными числами могут быть разной длины. Например, отрезок [0.25, 0.75] представляет собой участок прямой, который начинается с числа 0.25 и заканчивается числом 0.75. Длина этого отрезка равна 0.5.

Важно понимать, что отрезок с дробными числами может быть бесконечным, то есть не иметь определенного конца. Например, отрезок [0.1, ∞) представляет собой участок прямой, который начинается с числа 0.1 и не имеет конечного числа в качестве конца.

Отрезки с дробными числами широко используются в различных областях математики и науки, таких как статистика, физика и экономика. Они помогают представлять и анализировать различные величины и интервалы значений.

Видео по теме:

Вопрос-ответ:

Что такое отрезок в математике?

Отрезок – это часть прямой, ограниченная двумя точками.

Какие свойства имеет отрезок?

Отрезок имеет длину, которая определяется расстоянием между его конечными точками. Отрезки могут быть равными, если их длины совпадают, или не равными, если их длины различаются.

Как записывается отрезок на плоскости?

Отрезок на плоскости может быть записан с помощью двух точек, которые являются его начальной и конечной точками. Например, отрезок AB.

Какие примеры отрезков можно привести?

Примерами отрезков могут быть отрезки, соединяющие две вершины многоугольника, отрезки, соединяющие две точки на окружности, или отрезки, которые отмечают расстояние между двумя домами.

Какие еще понятия связаны с отрезками в математике?

С отрезками связаны такие понятия, как середина отрезка, которая находится точно посередине между его конечными точками, и отрезок, который является частью большего отрезка.

Что такое отрезок?

Отрезок — это часть прямой, состоящая из двух точек — начальной и конечной. Отрезок имеет длину, которую можно измерить с помощью линейки.

Как определить отрезок на прямой?

Чтобы определить отрезок на прямой, нужно указать начальную и конечную точки этого отрезка. Например, отрезок AB будет состоять из двух точек A и B, где A — начальная точка, а B — конечная точка.

Отрезки с отрицательными числами

Пример 1:

ОтрезокОбозначениеЧисла на отрезке

[-5, 3]

От -5 до 3

-5, -4, -3, -2, -1, 0, 1, 2, 3

В данном примере мы имеем отрезок, который начинается с числа -5 и заканчивается числом 3. Все числа на данном отрезке являются отрицательными или равны нулю. Такой отрезок может быть представлен на числовой прямой следующим образом:

Пример 2:

ОтрезокОбозначениеЧисла на отрезке

[-2, -1]

От -2 до -1

-2, -1

В данном примере отрезок содержит только два числа: -2 и -1. Оба числа находятся в отрицательной области числовой прямой. Такой отрезок может быть представлен на числовой прямой следующим образом:

Таким образом, отрезки с отрицательными числами представляют собой участки числовой прямой, где значения могут быть только отрицательными числами или равными нулю.

Практическое применение отрезков в математике

ПримерОписание

Строительство дома	При проектировании и строительстве дома отрезки используются для измерения расстояний. Например, для определения длины стены, ширины комнаты или высоты потолка.
Торговля	В торговле отрезки используются для вычисления длины товаров или расстояния между торговыми точками. Например, для измерения длины ткани или ширины полки в магазине.
География	В географии отрезки используются для измерения расстояний между городами, озерами или другими географическими объектами. Например, для определения расстояния между двумя городами на карте.
Использование времени	Временные отрезки используются для измерения временных интервалов. Например, для определения длительности фильма или времени, затраченного на выполнение задания.

Это лишь несколько примеров применения отрезков в математике. Отрезки широко используются в различных областях, и понимание этого понятия является важным для решения различных задач.