Что такое вращательное движение в математике определение

Вращательное движение в математике — это форма движения, при которой объект вращается вокруг некоторой оси. Определение вращательного движения включает понятия углового перемещения, угловой скорости и углового ускорения. Понимание вращательного движения в математике важно для анализа и моделирования различных физических и инженерных систем.

Вращательное движение — это одно из основных понятий в математике, которое описывает движение тела вокруг оси. Оно является важной составляющей механики и находит широкое применение в различных областях, таких как физика, инженерия, аэрокосмическая промышленность и даже в компьютерной графике.

Для полного понимания вращательного движения необходимо знать основные понятия, такие как ось вращения, угловая скорость, момент инерции и момент сил. Ось вращения — это воображаемая линия, вокруг которой происходит вращение тела. Угловая скорость — это величина, определяющая скорость изменения угла поворота тела вокруг оси вращения. Момент инерции — это мера инертности тела относительно оси вращения и зависит от его формы и распределения массы. Момент сил — это векторная величина, определяющая вращательное воздействие силы на тело.

Примером вращательного движения может служить вращение земли вокруг своей оси. Земля вращается с постоянной угловой скоростью в течение 24 часов, что приводит к чередованию дня и ночи. Ось вращения земли проходит через северный и южный полюс.

Вращательное движение также проявляется в поведении множества других объектов, например, вращение колеса автомобиля, вращение винта винтовки, вращение космического спутника вокруг планеты и многое другое. Изучение вращательного движения позволяет более глубоко понять и предсказывать поведение таких объектов, а также разрабатывать эффективные технические решения.

Определение вращательного движения

Основные понятия, связанные с вращательным движением, включают:

• Ось вращения — линия, вокруг которой происходит вращение тела.
• Угловая скорость — скорость изменения угла поворота тела вокруг оси вращения.
• Момент силы — величина, характеризующая вращательное движение и равная произведению силы, приложенной к телу, на плечо силы, то есть расстояние от оси вращения до точки приложения силы.
• Момент инерции — физическая величина, характеризующая инертность тела относительно его вращения вокруг заданной оси. Он зависит от массы и геометрических параметров тела.
• Момент импульса — векторная величина, равная произведению момента инерции тела на его угловую скорость.

Примеры вращательного движения включают:

• Вращение планет вокруг своих осей.
• Вращение колеса автомобиля.
• Вращение спиннера вокруг своей оси.
• Вращение винта в шнековом транспортере.

Вращательное движение широко используется в науке, технике и повседневной жизни. Оно играет важную роль в механике, динамике и дизайне различных устройств и механизмов.

Вращение в математике: основные понятия

Основные понятия, связанные с вращением:

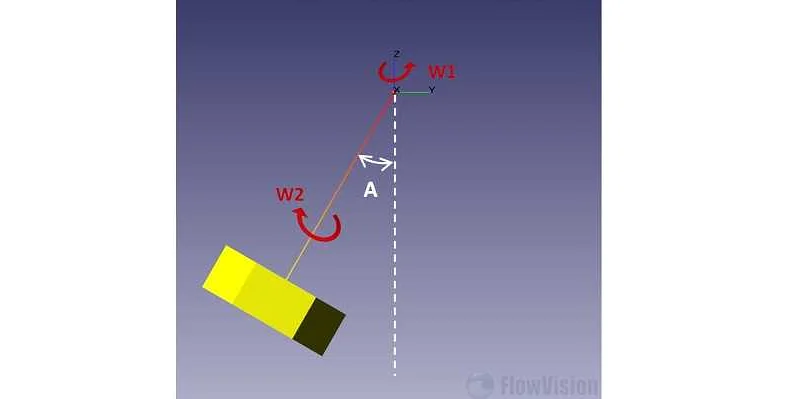
• Ось вращения — это прямая линия или линия в пространстве, вокруг которой происходит вращение. Ось вращения может быть горизонтальной, вертикальной или проходить через любую точку в пространстве.
• Угол поворота — это мера вращения объекта вокруг оси. Угол поворота измеряется в градусах или радианах и определяет, насколько объект повернулся относительно исходного положения.
• Точка вращения — это фиксированная точка, которая остается неподвижной при вращении объекта. Вокруг этой точки все остальные точки объекта поворачиваются.
• Вектор вращения — это вектор, который указывает направление оси вращения и определяет ориентацию вращения. Вектор вращения имеет длину и направление.

Примеры вращения в математике:

• Вращение стрелки на диаграмме с часами вокруг центра диска.
• Вращение колеса вокруг своей оси при движении автомобиля.
• Вращение Земли вокруг своей оси, вызывающее смену дня и ночи.
• Вращение спутника вокруг планеты.

Изучение вращения в математике позволяет анализировать движение объектов, определять их положение в пространстве и решать задачи, связанные с геометрией и физикой.

Ось вращения и ее свойства

Свойства оси вращения включают:

• Неподвижность точек: все точки, лежащие на оси вращения, не перемещаются в процессе вращения.
• Однородность вращения: вокруг оси вращения объект вращается с постоянной угловой скоростью, что означает, что все точки объекта совершают полные обороты вокруг оси за одинаковые промежутки времени.
• Перпендикулярность к поверхности: ось вращения перпендикулярна плоскости объекта и лежит внутри или на поверхности объекта.

Знание оси вращения позволяет лучше понять и описать характеристики вращательного движения объекта, такие как угловая скорость и момент инерции.

Угловая скорость и угловое ускорение

Вращательное движение тела характеризуется не только углом поворота, но и скоростью поворота. Угловая скорость (ω) определяется как отношение изменения угла поворота (Δθ) к промежутку времени (Δt), в течение которого происходит поворот:

ω = Δθ/Δt

Единицей измерения угловой скорости в системе СИ является радиан в секунду (рад/с).

Угловое ускорение (α) определяется как изменение угловой скорости (Δω) в единицу времени:

α = Δω/Δt

Единицей измерения углового ускорения в системе СИ также является радиан в секунду в квадрате (рад/с²).

Угловая скорость и угловое ускорение являются величинами, характеризующими изменение ориентации тела в пространстве во времени. Они играют важную роль в изучении вращательных движений твердого тела, а также в различных областях науки и техники, где вращение является существенной составляющей процесса.

Момент инерции и его роль в вращательном движении

Момент инерции обозначается буквой I и вычисляется по формуле:

I = ∑(mᵢ * rᵢ²)

где mᵢ — масса i-го элемента тела, rᵢ — расстояние от оси вращения до i-го элемента.

Чем больше момент инерции, тем труднее изменить вращение тела. Если момент инерции равен нулю, то тело не может вращаться вокруг данной оси.

Момент инерции играет важную роль во многих задачах, связанных с вращательным движением. Например, при расчете кинетической энергии вращающегося тела используется формула:

E = (1/2) * I * ω²

где E — кинетическая энергия, I — момент инерции, ω — угловая скорость вращения тела.

Также, момент инерции может использоваться для определения момента силы, действующей на вращающееся тело, по формуле:

M = I * α

где M — момент силы, I — момент инерции, α — угловое ускорение.

Таким образом, момент инерции является важным показателем при изучении и анализе вращательного движения твердого тела.

Закон сохранения момента импульса

Вращательное движение тела вокруг неподвижной оси сопровождается изменением момента импульса. Согласно закону сохранения момента импульса, если на тело не действуют внешние моменты сил, то момент импульса остается постоянным.

Этот закон можно выразить следующим образом: сумма моментов импульса всех частей системы относительно некоторой оси равна производной по времени от момента импульса всей системы относительно этой же оси.

Из закона сохранения момента импульса следует, что если система изолирована от внешних воздействий, то момент импульса остается постоянным во времени.

Примером применения закона сохранения момента импульса может служить вращение планет вокруг своих осей. Поскольку на планеты практически не действуют внешние моменты сил, их момент импульса остается постоянным. Это обеспечивает стабильное и регулярное вращение планет вокруг своих осей.

Видео по теме:

Вопрос-ответ:

Как определить вращательное движение?

Вращательное движение определяется как движение объекта вокруг оси, при котором все его точки описывают окружности с одинаковой угловой скоростью.

Какие основные понятия связаны с вращательным движением?

Основными понятиями вращательного движения являются угловая скорость, момент инерции и момент силы.

Можете привести примеры объектов, которые движутся с вращательным движением?

Примерами объектов, движущихся с вращательным движением, могут быть колесо автомобиля, каток на коньках или вращающийся винт винтовки.

Как связаны линейная и угловая скорости вращательного движения?

Линейная скорость точки на вращающемся объекте равна произведению угловой скорости на радиус, по которому движется эта точка.

Примеры вращательного движения в природе и технике

Вращательное движение встречается во многих явлениях природы и технике. Ниже приведены несколько примеров:

1. Вращение Земли вокруг своей оси. Это явление наблюдается каждый день, когда Земля вращается, создавая смену дня и ночи.
2. Вращение планет вокруг Солнца. Планеты движутся по орбитам вокруг Солнца, при этом совершая вращательное движение.
3. Вращение электронов в атомах. В атомах электроны вращаются вокруг ядра, образуя электронные облака.
4. Вращение ветряных мельниц. Ветряные мельницы преобразуют кинетическую энергию ветра во вращательное движение лопастей и затем в механическую работу.
5. Вращение колес автомобилей. Колеса автомобилей вращаются при движении, обеспечивая передвижение и устойчивость.

Это лишь некоторые примеры, демонстрирующие вращательное движение как в природе, так и в технике. Это явление широко используется для передачи энергии, создания движения и обеспечения функциональности различных устройств и систем.

Роль вращательного движения в механике и физике

Вращательное движение широко применяется для описания поведения объектов в механике и физике. Оно позволяет моделировать и анализировать движение твердых тел, таких как вращение колеса, вращение земли вокруг своей оси, вращение планет вокруг солнца и многие другие явления.

Вращательное движение имеет свои особенности, которые отличают его от прямолинейного движения. Оно характеризуется угловой скоростью, угловым ускорением и моментом инерции. Угловая скорость показывает, как быстро тело вращается вокруг оси, угловое ускорение показывает изменение угловой скорости со временем, а момент инерции характеризует распределение массы тела относительно оси вращения.

Вращательное движение имеет множество применений в различных областях науки и техники. В механике оно используется для описания движения вращающихся механизмов, таких как двигатели, турбины, ветряки. В физике оно применяется для изучения гироскопических явлений, вращающихся систем и многих других физических процессов.

Понимание вращательного движения является важной частью физической и механической подготовки и позволяет увидеть и объяснить множество явлений, которые не могут быть описаны только прямолинейным движением. Изучение вращательного движения позволяет строить более точные модели и прогнозировать поведение систем вращающихся тел.