Что такое вращательное движение в математике

Вращательное движение в математике – это форма движения, при которой объект или система поворачивается вокруг оси. В этой статье мы рассмотрим основные понятия и принципы вращательного движения, а также приведем примеры его применения в различных областях математики.

Вращательное движение — это тип движения, при котором объект вращается вокруг некоторой оси. Оно является одним из фундаментальных понятий в математике и физике, и находит широкое применение в различных областях науки и техники.

Вращательное движение можно наблюдать во многих ежедневных явлениях, например, когда колесо автомобиля вращается, велосипедист совершает поворот или планеты вращаются вокруг своих осей. Основные характеристики вращательного движения — это угловая скорость и угловое ускорение, которые определяют скорость и ускорение вращения объекта.

Примером вращательного движения может служить вращение мяча во время игры в баскетбол. Когда игрок бросает мяч, он начинает вращаться вокруг своей оси, что обусловлено приложенным к нему моментом силы. Вращательное движение мяча позволяет ему перемещаться по траектории, образующей параболу.

Особенностью вращательного движения является то, что объекты вращаются вокруг оси, которая может быть фиксированной или изменяемой. Кроме того, вращательное движение может быть равномерным или неравномерным, в зависимости от того, как изменяется угловая скорость объекта со временем.

Вращательное движение имеет много приложений в научных и технических областях. Например, оно используется в механике для моделирования поведения вращающихся систем, в технике для создания механизмов и приводов, а также в астрономии для изучения движения планет и звезд.

Что такое вращательное движение в математике?

Вращательное движение имеет свои особенности и характеристики. Одной из основных характеристик вращательного движения является угловая скорость, которая определяет скорость вращения объекта вокруг оси. Угловая скорость измеряется в радианах в секунду и может быть постоянной или изменяться со временем.

Другой важной характеристикой вращательного движения является угловое ускорение, которое определяет изменение угловой скорости со временем. Угловое ускорение измеряется в радианах в секунду в квадрате и может быть постоянным или изменяться.

Примерами вращательного движения могут служить вращение колеса автомобиля, вращение спирали на шнеке винтовой лестницы или вращение планет вокруг Солнца. Вращательное движение также встречается во многих других областях, таких как физика, механика и техника.

Видео по теме:

Определение и особенности вращательного движения

Особенности вращательного движения включают:

1. Угловую скорость: вращательное движение характеризуется угловой скоростью, которая измеряет скорость изменения угла поворота тела относительно оси вращения. Угловая скорость обычно выражается в радианах в секунду.
2. Момент силы: для поддержания вращательного движения необходимо приложение момента силы. Момент силы определяет величину и направление вращательного движения тела. Он равен произведению силы, действующей на тело, на перпендикулярное расстояние от оси вращения до линии действия силы.
3. Момент инерции: момент инерции является мерой инертности тела относительно оси вращения. Он зависит от формы, размера и распределения массы тела. Чем больше момент инерции, тем труднее изменить скорость вращения тела.
4. Закон сохранения момента импульса: вращательное движение подчиняется закону сохранения момента импульса, по которому сумма моментов импульса всех частей системы остается постоянной, если нет внешних моментов сил.

Вращательное движение является важным понятием в математике и физике, и оно находит применение в различных областях, от механики и динамики до астрономии и инженерии.

Примеры применения вращательного движения

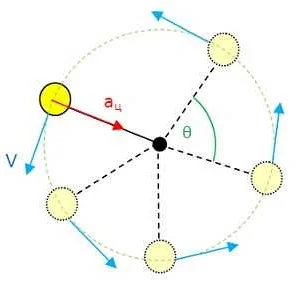
Вращательное движение находит широкое применение в различных областях науки и техники. Вот некоторые примеры его использования:

• Механика: вращательное движение используется для описания движения вращающихся тел, таких как колеса, роторы, валы и шестерни. Оно позволяет анализировать и предсказывать их поведение и свойства.
• Физика: вращательное движение играет важную роль в объяснении явлений, связанных с моментом импульса и сохранением углового момента. Оно помогает понять свойства вращающихся систем, таких как гироскопы и спутники.
• Инженерия: вращательное движение используется при проектировании и разработке механизмов и машин, которые требуют вращения для своей работы. Примеры включают в себя двигатели, турбины, ветрогенераторы и приводы.
• Робототехника: вращательное движение применяется для управления и перемещения роботов. Оно позволяет им достичь определенных позиций и ориентации в пространстве, а также выполнять задачи, требующие точного вращения.
• Астрономия: вращательное движение играет ключевую роль в изучении и моделировании движения планет, звезд и галактик. Оно помогает понять формирование и эволюцию космических объектов.

Примеры применения вращательного движения можно найти во многих других областях науки и техники. Это мощный и универсальный инструмент, который помогает нам понять и контролировать движение вращающихся систем.

Изучение вращательного движения в геометрии

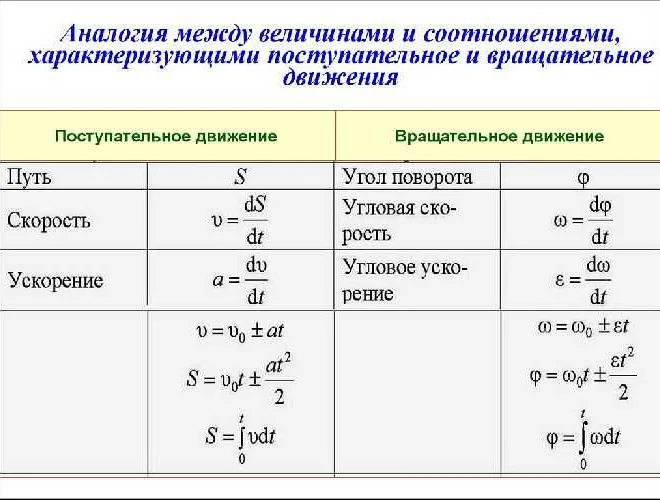
Для изучения вращательного движения используются различные геометрические понятия и инструменты. Одним из таких понятий является понятие вращательной симметрии, которая описывает сохранение формы фигуры при ее вращении вокруг оси. Вращательная симметрия является одним из фундаментальных принципов геометрии и находит широкое применение в различных областях науки и техники.

Другим важным понятием, используемым при изучении вращательного движения, является момент инерции. Момент инерции определяет сопротивление фигуры изменению своего состояния вращения. Чем больше момент инерции, тем сложнее изменить скорость вращения фигуры. Изучение момента инерции позволяет определить, как изменяется энергия вращательного движения системы.

Вращательное движение находит применение в различных областях, включая физику, механику, аэродинамику и другие. Оно играет существенную роль в понимании и описании различных явлений и процессов. Изучение вращательного движения в геометрии позволяет расширить знания о пространственных формах и их свойствах, а также применить их в практических задачах.

Вращательное движение в физике и механике

Вращательное движение широко применяется в физике и механике для изучения поведения тел при вращении. Оно описывается различными физическими величинами, такими как угловая скорость, момент инерции и момент силы.

Угловая скорость – это физическая величина, которая определяет скорость изменения угла поворота тела в единицу времени. Она измеряется в радианах в секунду (рад/с).

Момент инерции – это физическая величина, которая характеризует инертность тела при вращении относительно определенной оси. Он зависит от формы и массы тела, а также от распределения массы относительно оси вращения.

Момент силы – это физическая величина, которая описывает вращающее действие силы относительно определенной оси. Он зависит от силы, приложенной к телу, и от расстояния от оси вращения до точки приложения силы.

Вращательное движение важно для понимания различных явлений и процессов, таких как вращение планет, движение ротора электродвигателя, колебания маятника и многих других. Оно позволяет рассчитывать и предсказывать их характеристики и свойства.

Изучение вращательного движения имеет большое значение не только в физике, но и в других науках и технических областях, таких как инженерия, аэродинамика, робототехника и другие. Понимание его принципов и законов позволяет разрабатывать и улучшать различные устройства, механизмы и технологии.

Вращательное движение в физике и механике является одной из основных тем для изучения и представляет собой важную составляющую для понимания множества явлений и процессов в природе и технике.

Математические модели вращательного движения

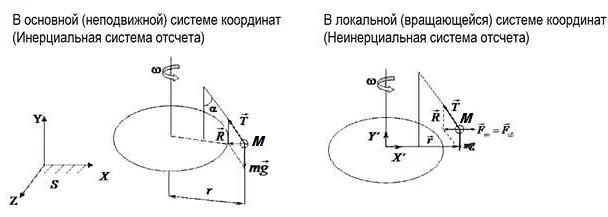
Одной из наиболее распространенных моделей вращательного движения является модель ротационного тела. В этой модели представляется, что тело вращается вокруг некоторой оси, и его движение может быть описано с помощью угловых координат и параметров, таких как момент инерции и угловая скорость.

Другой математической моделью вращательного движения является модель вращающегося маятника. В этой модели рассматривается движение маятника, который может вращаться вокруг оси. При этом его движение может быть описано с помощью угловых координат, момента инерции и угловой скорости.

Также существуют и другие математические модели, которые позволяют описать вращательное движение различных систем и объектов. Каждая из этих моделей имеет свои особенности и применяется в зависимости от конкретной задачи или объекта вращения.

Использование математических моделей вращательного движения позволяет проводить анализ и расчеты, определять закономерности и прогнозировать поведение вращающихся систем. Это важно для понимания и изучения различных физических явлений, а также для разработки и улучшения различных технических устройств и механизмов.

Применение вращательного движения в технике и технологиях

Одним из примеров применения вращательного движения в технике является использование роторов в электрических двигателях. Роторы вращаются под воздействием электрического тока, что позволяет преобразовывать электрическую энергию в механическую. Это позволяет создавать двигатели, которые используются в самых разных устройствах, от бытовых электроприборов до мощных промышленных механизмов.

Вращательное движение также играет важную роль в автомобильной промышленности. Колеса автомобилей вращаются, обеспечивая передвижение автомобиля. Кроме того, вращаются двигатели, передачи и другие механизмы, придающие движение автомобилю.

Кроме того, вращательное движение применяется в медицине. Например, применение вращательного движения используется в хирургии при использовании бормашин, которые вращаются с высокой скоростью и используются для прочистки костей или удаления опухолей.

Вращательное движение также находит применение в процессе производства. Например, вращательное движение используется в мельницах и станках, где вращение осей обеспечивает обработку материалов или создание деталей. Вращение также используется в процессе сварки, где вращение предмета сварки обеспечивает равномерное нагревание и соединение деталей.

Таким образом, вращательное движение является важным элементом в технике и технологиях. Оно применяется в различных областях и играет ключевую роль в процессе преобразования энергии и создании механизмов, обеспечивающих передвижение, обработку материалов и другие технические процессы.

Практическое значение вращательного движения в различных областях

Вращательное движение имеет широкое практическое применение в различных областях науки и техники. Ниже приведены некоторые примеры, где вращательное движение играет важную роль:

1. Механика: вращательное движение используется для описания движения твердых тел, таких как колеса, валы и роторы. Оно позволяет анализировать законы сохранения момента импульса и энергии во время вращения.
2. Машиностроение: вращательное движение является основой для создания различных механизмов, включая двигатели, турбины и редукторы. Оно позволяет передавать и преобразовывать механическую энергию.
3. Электротехника: вращательное движение применяется в электрических машинах, таких как генераторы и электродвигатели. Оно позволяет преобразовывать электрическую энергию в механическую и наоборот.
4. Аэрокосмическая техника: вращательное движение используется в вертолетах, космических аппаратах и других летательных аппаратах. Оно позволяет изменять ориентацию и стабилизировать положение объектов в космосе и атмосфере.
5. Медицина: вращательное движение применяется в медицинской технике для создания медицинских инструментов, таких как стоматологические сверла и бормашины. Оно позволяет эффективно выполнять различные процедуры.

Вращательное движение имеет большое практическое значение и играет важную роль во многих областях, способствуя развитию техники и науки.

Вопрос-ответ:

Что такое вращательное движение?

Вращательное движение — это тип движения, при котором тело вращается вокруг определенной оси.

Как определить вращательное движение?

Вращательное движение можно определить по изменению ориентации тела в пространстве и по наличию оси вращения.

Какие примеры вращательного движения существуют?

Примерами вращательного движения могут служить вращение планет вокруг своих осей, вращение колеса автомобиля, вращение маховика.

Как связано вращательное движение с математикой?

Вращательное движение тесно связано с математикой, так как оно описывается с помощью уравнений и формул, которые позволяют определить скорость и ускорение вращения тела.

Какие особенности имеет вращательное движение?

Особенности вращательного движения включают определение момента инерции, уравнения движения, сохранение момента импульса и энергии вращения, а также наличие центробежной силы.

Что такое вращательное движение?

Вращательное движение — это движение тела или системы тел, при котором каждая точка описывает окружность или дугу окружности вокруг определенной оси в пространстве.

Как определить скорость точки при вращательном движении?

Скорость точки при вращательном движении определяется векторно, как векторное произведение радиус-вектора точки на вектор угловой скорости.