Что такое вспомогательные модели в математике

Вспомогательные модели в математике представляют собой математические объекты, созданные для упрощения сложных задач и анализа сложных систем. Они помогают увидеть основные закономерности и связи в данных, а также предоставляют инструменты для решения конкретных задач. Вспомогательные модели широко используются в различных областях науки, техники и экономики, позволяя более точно предсказывать и анализировать различные явления и процессы.

Математика — это одна из наиболее фундаментальных наук, которая описывает законы и структуры вселенной. Однако в реальном мире часто возникают сложные проблемы, которые трудно решить с помощью только общих математических теорий и понятий.

В таких ситуациях ученые прибегают к использованию вспомогательных моделей. Вспомогательная модель — это упрощенная математическая модель, которая позволяет аппроксимировать реальную систему и проводить исследования и эксперименты.

Вспомогательные модели являются неотъемлемой частью математического исследования и имеют особое значение во многих областях науки и техники. Они позволяют ученым анализировать сложные системы, прогнозировать их поведение и разрабатывать новые технологии и методы решения проблем.

Вспомогательные модели позволяют ученым разобраться в сложных процессах, упростить математические вычисления и получить качественные результаты. Они помогают сделать науку более доступной и понятной и играют важную роль в развитии научно-технического прогресса.

Определение вспомогательных моделей в математике и их правильное использование являются важными навыками для каждого ученого и инженера. Это позволяет им решать сложные задачи, находить новые решения и применять математические методы в различных областях жизни и деятельности.

Вспомогательные модели в математике

Вспомогательные модели играют важную роль в математике, помогая упростить сложные задачи и решить различные проблемы. Они представляют собой упрощенные или абстрактные версии реальных объектов или явлений, которые можно изучать и анализировать с помощью математических методов.

Одна из основных целей вспомогательных моделей — облегчить понимание и решение математических задач. Они могут представлять сложные физические системы, экономические процессы, социальные взаимодействия и многое другое. Вспомогательные модели помогают исследователям упростить и абстрагировать реальные объекты или явления, чтобы сосредоточиться на ключевых аспектах их поведения или свойствах.

Вспомогательные модели могут быть представлены в виде уравнений, графиков, графов или других математических структур. Они позволяют исследователям проводить эксперименты и анализировать результаты, не трогая реальные объекты или явления. Благодаря этому, исследователи могут прогнозировать и предсказывать различные сценарии и исследовать разные варианты решений, прежде чем применять их на практике.

Одним из наиболее известных примеров вспомогательных моделей в математике является график функции. График функции представляет собой графическое представление зависимости между входными и выходными значениями функции. Он позволяет исследователям визуализировать и анализировать функцию, понять ее поведение и свойства, и использовать эту информацию для решения различных задач.

Вспомогательные модели являются неотъемлемой частью математического анализа, их использование позволяет исследователям и ученым лучше понять и объяснить сложные явления и проблемы. Они играют важную роль в различных областях, включая физику, экономику, социологию и другие науки. Без вспомогательных моделей математический анализ был бы значительно сложнее и менее эффективным инструментом для изучения и понимания реального мира.

Видео по теме:

Определение вспомогательных моделей

Вспомогательные модели могут быть графическими, символическими или алгебраическими, в зависимости от задачи, которую они помогают решить. Они могут служить для упрощения математических вычислений, представления информации или анализа данных.

Одним из примеров вспомогательной модели является график функции. График позволяет визуализировать зависимость между входными и выходными значениями функции, что помогает понять ее поведение и решить различные задачи, связанные с этой функцией.

Вспомогательные модели также могут использоваться для представления физических процессов или явлений. Например, модель баллистической кривой может помочь предсказать траекторию полета снаряда или ракеты.

Важность вспомогательных моделей в математике заключается в том, что они позволяют упростить сложные задачи и сделать их более понятными и доступными для анализа. Они помогают нам лучше понять основные концепции и принципы, лежащие в основе математических моделей, и применить их к различным областям знаний.

Таким образом, вспомогательные модели играют важную роль в математике, позволяя нам более глубоко исследовать и понимать сложные математические задачи и явления.

Роль вспомогательных моделей в математике

Вспомогательные модели играют важную роль в математике, позволяя упростить и абстрагировать сложные математические концепции и проблемы. Они помогают нам лучше понять и исследовать различные явления и процессы, используя математические методы и инструменты.

Вспомогательные модели могут быть представлены в виде упрощенных математических формул, графиков, диаграмм или других графических представлений. Они позволяют нам сделать сложные математические концепции более доступными и понятными, а также помогают нам визуализировать и проверять наши гипотезы и предсказания.

Кроме того, вспомогательные модели могут быть использованы для прогнозирования и предсказания различных явлений. Они позволяют нам проводить эксперименты и моделировать различные ситуации, чтобы предсказать их исходы и оценить возможные риски и выгоды.

Вспомогательные модели также позволяют нам разрабатывать новые математические методы и алгоритмы, которые могут быть использованы для решения сложных задач и проблем. Они помогают нам лучше понять структуру и свойства математических объектов и явлений, что в свою очередь способствует развитию математической науки.

Таким образом, вспомогательные модели играют неотъемлемую роль в математике, помогая нам лучше понять и исследовать различные явления и проблемы, а также разрабатывать новые математические методы и алгоритмы.

Вопрос-ответ:

Зачем в математике нужны вспомогательные модели?

Вспомогательные модели в математике используются для упрощения и абстракции сложных математических концепций. Они помогают наглядно представить абстрактные понятия, упростить вычисления и решение задач.

Какие примеры вспомогательных моделей в математике можно привести?

Примерами вспомогательных моделей в математике могут быть графики функций, геометрические фигуры, математические диаграммы, таблицы и т.д. Эти модели помогают визуализировать и анализировать математические концепции и данные.

Какую роль играют вспомогательные модели в обучении математике?

Вспомогательные модели играют важную роль в обучении математике. Они помогают учащимся лучше понять и запомнить математические концепции, развивают навыки анализа и решения задач, а также способствуют развитию логического мышления и креативности.

Какие преимущества имеет использование вспомогательных моделей в математике?

Использование вспомогательных моделей в математике позволяет упростить сложные концепции и вычисления, а также помогает визуализировать абстрактные понятия. Это позволяет лучше понять математические концепции и применять их на практике. Кроме того, вспомогательные модели способствуют развитию креативности и аналитического мышления.

Важность вспомогательных моделей в математике

Вспомогательные модели в математике играют важную роль в понимании и решении различных математических проблем. Они представляют собой упрощенные и абстрактные математические конструкции, которые помогают нам лучше понять и объяснить сложные математические концепции.

Одной из основных причин использования вспомогательных моделей является то, что они позволяют нам визуализировать математические идеи и отношения. Визуализация может значительно облегчить понимание математических концепций, особенно для студентов и других людей, которые только начинают изучать математику. Вспомогательные модели могут быть представлены в виде графиков, диаграмм, таблиц и других геометрических или числовых представлений.

Кроме того, вспомогательные модели позволяют нам проводить эксперименты и исследования, которые могут помочь нам лучше понять математические концепции. Моделирование позволяет нам рассмотреть различные варианты и ситуации, которые могут возникнуть в реальных или абстрактных математических проблемах. Это позволяет нам проверить гипотезы, сделать выводы и принять решения на основе полученных результатов.

Вспомогательные модели также играют важную роль в коммуникации математических идей. Они являются универсальным языком, который позволяет нам обмениваться идеями, объяснять сложные концепции и устанавливать связи между различными областями математики. Вспомогательные модели помогают нам создать общие обозначения и термины, которые делают математические идеи более доступными и понятными для всех.

В итоге, использование вспомогательных моделей в математике является неотъемлемой частью математического исследования и обучения. Они помогают нам лучше понять и объяснить сложные математические концепции, визуализировать идеи, проводить эксперименты и исследования, а также коммуницировать математические идеи и установить связи между различными областями математики. Вспомогательные модели помогают нам развивать наше математическое мышление и расширять наши знания и способности в области математики.

Примеры вспомогательных моделей в математике

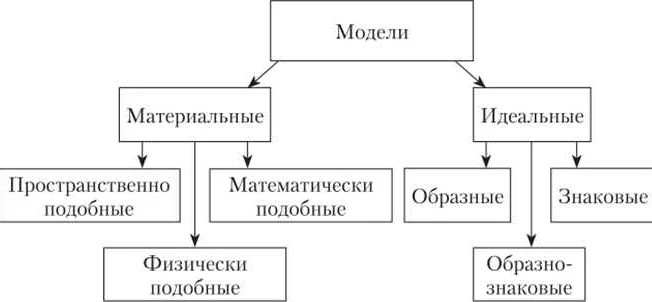
Вот несколько примеров вспомогательных моделей, широко используемых в математике:

МодельОписание

График	График — это визуальное представление зависимости между двумя переменными. Он позволяет увидеть, как изменяется одна переменная при изменении другой. Графики используются для анализа функций, решения уравнений и представления данных.
Геометрическая модель	Геометрическая модель — это абстрактное представление геометрических фигур и пространства. Она позволяет визуализировать и анализировать геометрические свойства и отношения между фигурами. Геометрические модели широко используются при изучении геометрии и решении задач построения фигур.
Матрица	Матрица — это таблица, состоящая из чисел или символов, расположенных в виде прямоугольной сетки. Матрицы используются для представления и анализа линейных операций, решения систем линейных уравнений и работе с многомерными данными.
Вероятностная модель	Вероятностная модель — это математическая модель, которая описывает случайные явления и предсказывает их вероятности. Вероятностные модели используются в статистике, теории вероятностей и других областях для анализа рисков, прогнозирования результатов и принятия решений.

Это лишь некоторые примеры вспомогательных моделей, которые широко применяются в математике. Они помогают упростить и визуализировать сложные математические концепции, что делает их понятными и доступными для анализа и применения.

Применение вспомогательных моделей в научных исследованиях

Вспомогательные модели позволяют исследователям упростить сложные системы и явления, разбивая их на более простые компоненты. Это помогает создать более точные и понятные представления о том, как работает реальный мир.

Одним из примеров применения вспомогательных моделей в научных исследованиях является моделирование климатических изменений. Климат является сложной системой, исследование которой требует учета множества факторов. Вспомогательные модели позволяют исследователям упростить эту сложность, учитывая только самые важные факторы. Такие модели могут помочь улучшить наше понимание климатических изменений и предсказать их последствия.

Также вспомогательные модели широко применяются в физике, экономике, биологии и других научных дисциплинах. Они помогают исследователям упростить сложные процессы и явления, чтобы лучше понять их причины и следствия.

Использование вспомогательных моделей в научных исследованиях имеет несколько преимуществ. Во-первых, они позволяют исследователям упростить сложные явления, что помогает лучше понять их основные принципы. Во-вторых, они делают исследование более точным и предсказуемым, позволяя проверять гипотезы и прогнозировать результаты. В-третьих, вспомогательные модели позволяют исследователям применять различные методы и техники, которые могут быть неприменимы в реальных системах.

Вспомогательные модели в научных исследованиях играют важную роль в создании новых знаний и понимании сложных явлений. Они помогают исследователям разрабатывать новые гипотезы, тестировать их и делать выводы на основе полученных результатов.

Взаимосвязь вспомогательных моделей с другими математическими концепциями

Вспомогательные модели в математике играют важную роль в понимании и применении других математических концепций. Они часто используются для представления сложных или абстрактных идей в более конкретной и наглядной форме.

Одна из основных взаимосвязей вспомогательных моделей с другими математическими концепциями — это создание аналогий и связей между различными областями математики. Например, модель шарика, который движется по параболе, может помочь понять параболическую траекторию движения объекта в физике или в других областях математики, таких как геометрия или алгебра.

Вспомогательные модели также позволяют увидеть связь между абстрактными математическими концепциями и реальными проблемами или явлениями. Например, модель распределения вероятностей может быть использована для анализа случайных событий в реальном мире, таких как бросание монетки или выбор случайного числа из заданного диапазона.

Кроме того, вспомогательные модели могут быть использованы для представления и анализа данных. Например, диаграмма рассеяния может помочь визуализировать взаимосвязь между двумя переменными и определить наличие линейной или нелинейной связи между ними.

Таким образом, вспомогательные модели играют важную роль в математике, помогая учащимся и исследователям лучше понять и применять другие математические концепции. Они позволяют связать абстрактные идеи с реальным миром и создать аналогии и связи между различными областями математики.

Критерии выбора вспомогательных моделей

При выборе вспомогательных моделей в математике следует учитывать ряд критериев, которые помогут определить, насколько эффективно данная модель будет выполнять свои функции. Рассмотрим несколько основных критериев выбора вспомогательных моделей:

КритерийОписание

Точность	Модель должна быть достаточно точной, чтобы соответствовать реальным данным и обеспечивать высокую степень предсказательной способности.
Простота	Модель должна быть простой и понятной для использования. Сложные модели могут быть трудными в понимании и применении.
Объяснимость	Модель должна быть способной объяснить полученные результаты. Чем более понятно модель объясняет свои выводы, тем легче ее применять и доверять ее результатам.
Гибкость	Модель должна быть гибкой и приспособленной к различным задачам. Чем больше возможностей у модели, тем более универсальным и эффективным она будет.
Эффективность	Модель должна быть эффективной в плане вычислительных ресурсов и времени работы. Чем быстрее модель выполняет свои задачи, тем более практичной и применимой она будет.

При выборе вспомогательной модели следует учитывать все вышеперечисленные критерии и находить баланс между ними. В конечном итоге, выбор модели будет зависеть от конкретной задачи и требований, предъявляемых к ней.