Орлин б математика с дурацкими рисунками идеи которые формируют нашу реальность

Орлин б математика с дурацкими рисунками идеи которые формируют нашу реальность — увлекательная статья, в которой автор представляет свои необычные математические идеи, подкрепленные забавными рисунками. Узнайте, как математика может помочь вам лучше понять мир и формировать вашу реальность.

Математика — это наука, которая является фундаментом для понимания мира вокруг нас. Она описывает основные законы и принципы, которыми руководствуется наша реальность. Однако, иногда математические идеи могут показаться нелепыми и странными, особенно когда их представляют в виде дурацких рисунков.

Орлинб математика — это ветвь математики, которая занимается изучением абстрактных идей и их визуализацией. Эта концепция была разработана Орлинбом, известным математиком и художником, который привнес свежий взгляд на математические идеи. Он создал ряд дурацких рисунков, которые иллюстрируют сложные математические концепции и помогают нам лучше понять их.

Идеи, представленные в дурацких рисунках Орлинба, имеют глубокий смысл и влияют на нашу реальность. Они открывают новые горизонты для нашего понимания математики и помогают нам развивать свою интуицию и логическое мышление. Дурацкие рисунки Орлинба заставляют нас задуматься над тем, какие еще идеи и принципы могут быть скрыты за привычными законами и формулами.

Дурацкие рисунки Орлинба — это не только забавные картинки, но и способ проникнуть в самые глубины математической реальности. Они позволяют нам увидеть связи и взаимодействия между различными математическими концепциями и расширяют наше понимание окружающего нас мира.

Итак, орлинб математика с дурацкими рисунками представляет собой уникальный способ изучения и визуализации математических идей. Она помогает нам лучше понять, как математические концепции формируют нашу реальность и расширяют наше понимание мира. Дурацкие рисунки Орлинба открывают перед нами новые горизонты и вдохновляют нас на дальнейшие исследования и открытия в области математики.

Основы математики: первые шаги в понимании реальности

Первый шаг в нашем путешествии в мир математики — это понимание чисел и их свойств. Числа являются основой всей математики и используются повсюду в нашей повседневной жизни. Мы считаем деньги, измеряем расстояние, оцениваем вероятности — все это требует понимания чисел.

Следующий шаг — изучение операций с числами. Математика предлагает нам различные способы комбинирования чисел: сложение, вычитание, умножение и деление. Умение выполнять эти операции позволяет нам решать задачи и находить решения для различных проблем.

Однако математика — это не только числа и операции. Важную роль играют также геометрия и алгебра. Геометрия изучает формы, размеры и отношения между объектами, а алгебра работает с неизвестными и выражениями. Эти две области математики помогают нам анализировать и решать задачи, связанные с пространством и величинами.

Кроме того, математика имеет свои собственные правила и законы. Например, закон коммутативности говорит нам, что порядок слагаемых в сумме не имеет значения. Закон ассоциативности говорит нам, что результат операции не зависит от расстановки скобок. Знание этих правил помогает нам сделать точные и логические выводы.

Наконец, математика — это наука, в которой мы изучаем и создаем новые концепции и теории. Новые открытия в математике могут привести к новым технологиям и применениям, которые меняют нашу реальность.

Таким образом, понимание основ математики является необходимым условием для полноценного понимания мира вокруг нас. Оно помогает нам анализировать данные, решать проблемы и прогнозировать результаты. Независимо от того, каким образом мы используем математику, она является одним из ключей к пониманию реальности.

Визуализация и математика: как рисунки формируют наш мир

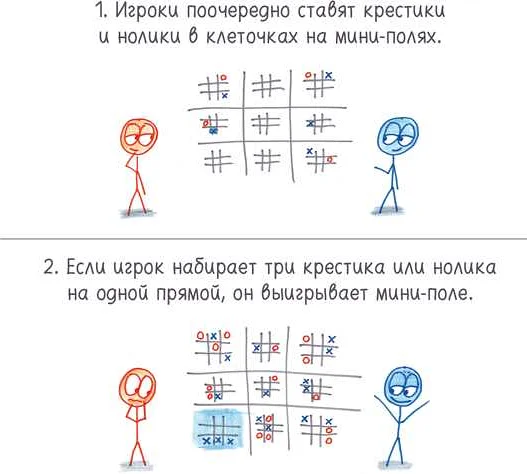
Рисунки и диаграммы могут быть использованы для иллюстрации математических теорем, законов и моделей. Они помогают нам увидеть связи и закономерности, которые в противном случае могли бы остаться незамеченными. Например, визуализация может показать нам геометрическую интерпретацию алгебраических уравнений или демонстрировать пространственные свойства математических объектов.

Кроме того, визуализация может быть полезной для объяснения сложных математических концепций и идей. Она может сделать абстрактные понятия более конкретными и понятными, помогая нам уловить суть их сущности. Например, с помощью диаграмм мы можем легко представить себе графы или функции и увидеть, как они работают.

Кроме того, визуализация может быть использована для исследования и открытия новых математических идей. Часто визуальная интуиция может помочь нам сформулировать гипотезы и найти новые паттерны и структуры в данных. Например, фрактальные рисунки помогли исследователям обнаружить новые математические закономерности.

Таким образом, визуализация играет важную роль в математике, помогая нам лучше понять и описать наш мир. Она позволяет нам увидеть скрытые закономерности и связи, а также делает абстрактные понятия более доступными и понятными. Поэтому использование рисунков и диаграмм является неотъемлемой частью математического исследования и образования.

Геометрия и пространство: ключевые понятия и их значимость

Одним из ключевых понятий в геометрии является понятие пространства. Пространство — это абстрактное понятие, описывающее местоположение и расположение объектов. Оно позволяет нам определить положение точки, линии или плоскости в отношении других объектов. Пространство имеет различные измерения, такие как двумерное, трехмерное и многомерное.

Другим важным понятием в геометрии является понятие формы. Форма — это геометрическая характеристика объекта, определяющая его внешний вид. Формы могут быть простыми, такими как прямоугольник или круг, или сложными, такими как фигуры в природе или абстрактные объекты.

Кроме того, геометрия также изучает понятие размера и измерения. Размер — это характеристика объекта, относящаяся к его длине, ширине или высоте. Измерение — это процесс определения размера с помощью единиц измерения, таких как сантиметры или метры.

Геометрия имеет широкую практическую значимость в различных областях науки и техники. Она используется в архитектуре для проектирования зданий, в геодезии для измерения земли, в физике для моделирования физических явлений, и в компьютерной графике для создания реалистичных изображений.

Таким образом, геометрия и понятия, связанные с пространством, формой, размером и измерением, играют важную роль в формировании нашей реальности. Они помогают нам понять и описать мир вокруг нас и находят применение во многих сферах нашей жизни.

Алгебра и анализ: инструменты для анализа реальности

Алгебра — это раздел математики, который изучает структуру и свойства математических объектов, таких как числа, алгебраические выражения и уравнения. Она помогает нам анализировать и решать различные задачи, связанные с количественными величинами. Алгебраические методы могут быть использованы для моделирования и решения различных реальных проблем, например, в физике, экономике и инженерии.

Анализ — это раздел математики, который изучает пределы, производные, интегралы и другие понятия, связанные с изменением и непрерывностью. Он позволяет нам анализировать и описывать различные процессы и явления в реальном мире. Аналитические методы могут быть применены для моделирования и предсказания поведения систем, таких как популяционная динамика, движение тел и физические законы.

Сочетание алгебры и анализа позволяет нам рассматривать реальность с разных точек зрения и строить более полные и точные модели. Математические методы позволяют нам выявлять закономерности, находить решения задач и предсказывать результаты. Они помогают нам анализировать данные, проводить эксперименты и принимать взвешенные решения.

Таким образом, алгебра и анализ являются неотъемлемыми инструментами для анализа и понимания реальности. Они помогают нам развивать логическое мышление, решать сложные задачи и строить более точные модели. Без них наше понимание мира было бы неполным, и мы бы не смогли обнаруживать и понимать глубинные закономерности, лежащие в основе нашей реальности.

Статистика и вероятность: понимание случайности и закономерностей

Статистика изучает количественные данные и является основой для проведения исследований. Она позволяет нам узнать, какие закономерности и связи существуют между различными явлениями. С помощью статистических методов мы можем анализировать данные, находить средние значения, распределения и тенденции в данных.

Вероятность, в свою очередь, изучает случайные события и их вероятность возникновения. Она позволяет нам оценить вероятность того или иного исхода и прогнозировать результаты. Вероятность может быть использована для принятия решений, основывающихся на статистических данных, а также для определения рисков и управления ими.

Понимание случайности и закономерностей является важным для многих областей науки и жизни. Например, в экономике статистика и вероятность используются для анализа рынка, прогнозирования тенденций и принятия решений в финансовой сфере. В медицине они помогают проводить исследования, определять эффективность лекарств и прогнозировать заболевания. В психологии они позволяют изучать поведение и мотивацию людей.

Таким образом, статистика и вероятность играют важную роль в нашем понимании реальности. Они помогают нам анализировать данные, делать выводы и прогнозировать события. Понимание случайности и закономерностей помогает нам принимать более обоснованные решения и управлять рисками.

Математические модели: отображение реальности в числах

Математические модели представляют собой формальные системы, состоящие из уравнений, функций и параметров. Они отображают реальность в виде математических выражений и позволяют нам анализировать и предсказывать различные сценарии поведения системы.

Одной из основных задач математического моделирования является построение модели, которая наиболее точно соответствует изучаемому явлению. Для этого математики и исследователи используют различные методы и подходы, включая дифференциальные уравнения, статистическую аналитику, графические модели и другие математические инструменты.

Математические модели позволяют нам предсказывать результаты экспериментов, определять зависимости и взаимосвязи между различными переменными, а также оптимизировать процессы и принимать обоснованные решения. Они играют важную роль в научных исследованиях, инженерных и технических проектах, финансовом анализе и многих других областях.

Важно отметить, что математические модели не являются полной идеальной копией реальности. Они лишь приближенно отражают сложные процессы и явления, учитывая основные факторы и закономерности. Однако, благодаря математическим моделям, мы можем увидеть скрытые закономерности, предсказать результаты и сделать значимые выводы.

Таким образом, математические модели являются мощным инструментом, который помогает нам лучше понять и описать реальность в числах и формулах. Они позволяют нам исследовать сложные системы, прогнозировать результаты и принимать взвешенные решения. Благодаря математическим моделям мы можем увидеть красоту и гармонию, лежащую в основе нашей реальности.

Видео по теме:

Вопрос-ответ:

Какие идеи формируют нашу реальность?

В статье рассматриваются различные идеи, которые влияют на формирование нашей реальности. Например, автор подчеркивает важность математики в понимании мира и приводит примеры, как математические модели помогают объяснить различные явления. Также обсуждается роль визуализации и рисунков в математике, которые помогают нам лучше понять абстрактные понятия и связи между ними. Важным аспектом является также философия и ее влияние на наше восприятие и понимание реальности.

Как математика помогает объяснить различные явления?

Математика является мощным инструментом для объяснения различных явлений в нашем мире. Она позволяет нам анализировать данные, находить закономерности и устанавливать причинно-следственные связи. Например, при изучении физических явлений математические модели помогают предсказывать результаты экспериментов и строить сложные системы уравнений, описывающие поведение объектов. Также математика применяется в экономике, социологии, биологии и других науках для анализа данных и разработки моделей.

Как визуализация и рисунки помогают нам понять математические понятия?

Визуализация и рисунки играют важную роль в понимании математических понятий. Они позволяют нам увидеть связи между абстрактными объектами и представить сложные концепции в более наглядной форме. Рисунки могут помочь визуализировать геометрические фигуры, графики функций, а также сложные структуры, такие как графы или сети. Благодаря визуализации мы лучше понимаем взаимосвязи между объектами и можем проще усваивать математические понятия.

Какие идеи формируют нашу реальность?

В статье рассматриваются различные идеи, которые влияют на формирование нашей реальности. Некоторые из них включают в себя концепции математики, физики, философии и искусства. Автор подчеркивает важность понимания этих идей для осознания того, как мы взаимодействуем с окружающим миром.

Какие рисунки используются в статье?

В статье используются рисунки, которые автор называет «дурацкими». Они являются простыми и схематичными, но при этом аккуратно иллюстрируют основные идеи, о которых говорится в тексте. Рисунки помогают визуализировать концепции и делают их более доступными для понимания.

Какие научные дисциплины оказывают влияние на формирование нашей реальности?

В статье упоминаются несколько научных дисциплин, которые влияют на формирование нашей реальности. Одной из таких дисциплин является математика, которая играет важную роль в понимании законов природы и описании физических явлений. Философия также влияет на нашу реальность, помогая нам осмыслить мир и наше место в нем. Искусство также играет свою роль в формировании нашей реальности, расширяя наше воображение и восприятие.

Почему автор называет рисунки «дурацкими»?

Автор называет рисунки «дурацкими», чтобы подчеркнуть их простоту и схематичность. Это не оскорбление, а скорее способ описания их упрощенного стиля. Рисунки в статье являются аккуратными и наглядными, их цель — иллюстрировать основные идеи и сделать их более доступными для понимания.

Компьютерное моделирование: роль математики в современных технологиях

Математика играет ключевую роль в компьютерном моделировании, поскольку она позволяет нам представить сложные физические, химические или биологические процессы в виде математических уравнений. Компьютеры затем используют эти уравнения для создания виртуальных моделей, которые можно исследовать и изменять.

Благодаря математике и компьютерному моделированию мы можем проводить эксперименты в виртуальной среде, что позволяет нам изучать и предсказывать поведение системы в различных условиях. Например, мы можем создать модель планетной системы и исследовать, как изменится ее структура и движение, если изменить массу одной из планет или величину гравитационной постоянной.

Компьютерное моделирование находит применение во многих областях, включая физику, химию, биологию, экологию, экономику и многие другие. Оно позволяет нам изучать сложные системы, которые трудно или невозможно исследовать в реальности. Кроме того, моделирование помогает нам разрабатывать новые технологии, оптимизировать процессы и прогнозировать результаты.

В заключение, математика играет незаменимую роль в современных технологиях, особенно в компьютерном моделировании. Она позволяет нам анализировать и предсказывать сложные явления и процессы, а также разрабатывать новые технологии и улучшать существующие.

Практическое применение математики: от науки до повседневной жизни

В науке математика используется для моделирования и понимания сложных физических и социальных явлений. Она помогает ученым анализировать данные, строить графики и прогнозировать результаты исследований. Математические модели используются в физике, химии, биологии, экономике и других науках, чтобы объяснить и предсказать различные процессы и явления.

В инженерии и технике математика является неотъемлемой частью проектирования и разработки новых технологий. Она помогает инженерам и архитекторам рассчитывать нагрузки, оптимизировать конструкции и предсказывать поведение систем. Математические модели используются для проектирования зданий, автомобилей, самолетов, компьютерных сетей и многих других технических систем.

В экономике и финансах математика используется для анализа данных, прогнозирования рыночных трендов и принятия решений. Математические модели помогают экономистам и финансистам оптимизировать инвестиции, управлять рисками и прогнозировать будущие результаты.

В повседневной жизни математика применяется во многих областях. Она помогает рассчитывать бюджет, управлять временем, планировать поездки и покупки, анализировать данные и принимать решения на основе числовых фактов. Математические навыки также полезны в изучении географии, музыки, спорта и других областей, где требуется анализ и логическое мышление.

Таким образом, математика играет важную роль в нашей жизни и помогает нам лучше понимать и управлять миром вокруг нас.