Что такое орт в математике

Орт — это математическое понятие, которое обозначает перпендикулярность или ортогональность двух векторов или плоскостей. Узнайте, как определить орт вектора или плоскости, а также какие свойства и примеры есть в математике.

Орт – это особый термин, который часто используется в математике. Орт является сокращением от слова «ортогональный», который означает «перпендикулярный» или «прямоугольный». В математике орт относится к векторам или функциям, которые ортогональны друг другу или образуют прямой угол.

Орт является очень важным понятием в математике, так как ортогональность используется во многих разделах, включая линейную алгебру, геометрию, физику и технические науки. Ортогональные векторы и функции имеют ряд свойств, которые делают их полезными в различных приложениях. Например, ортогональные векторы образуют базис в подпространстве, что позволяет представить любой вектор в этом подпространстве в виде линейной комбинации ортогональных векторов.

Ортогональность также играет важную роль в теории сигналов, обработке изображений, компьютерной графике и многих других областях науки и техники.

Примерами ортогональных векторов могут быть координатные оси в трехмерном пространстве (ось X, Y и Z), а также векторы, образующие углы 90 градусов друг с другом. Одним из примеров ортогональных функций являются синус и косинус, которые являются базисными функциями в тригонометрии и находят широкое применение в физике и инженерии.

В заключение, понятие орта в математике играет важную роль и используется во многих областях науки и техники. Ортогональные векторы и функции обладают определенными свойствами, которые делают их полезными в решении различных задач. Примеры ортогональных векторов и функций можно встретить в различных областях, таких как геометрия, физика и компьютерная графика.

Орт в математике: определение и свойства

В математике понятие «орт» относится к двум векторам, которые ортогональны друг другу. Ортогональность означает, что угол между этими векторами равен 90 градусам.

Орт может быть представлен в виде двухмерной таблицы, называемой матрицей. В этой матрице первый столбец представляет первый вектор, а второй столбец — второй вектор. Значения в матрице обозначаются числами и показывают длины векторов.

Свойства орта в математике:

СвойствоОписание

Ортогональность	Векторы, образующие орт, перпендикулярны друг другу.
Единичная длина	Длина каждого вектора в орте равна 1.
Линейная независимость	Векторы в орте являются линейно независимыми.

Примеры ортов в математике:

1. Стандартный орт в двумерном пространстве: первый вектор имеет координаты (1, 0), а второй вектор имеет координаты (0, 1).

2. Орт в трехмерном пространстве: первый вектор имеет координаты (1, 0, 0), второй вектор имеет координаты (0, 1, 0), а третий вектор имеет координаты (0, 0, 1).

Орты играют важную роль в математике, физике и других науках. Они используются для решения различных задач, связанных с векторами и пространствами.

Орт: основное понятие и его характеристики

Основные характеристики орта:

СвойствоОписание

Перпендикулярность	Орт перпендикулярен вектору или плоскости, с которым он сопряжен.
Единичная длина	Длина орта равна единице.
Нормализация	Процесс приведения вектора к единичной длине называется нормализацией. Орт всегда является нормализованным вектором.

Примеры ортов:

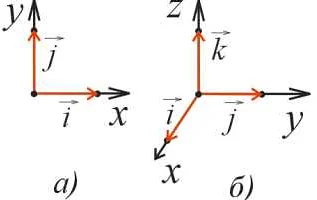
• Единичные векторы осей координат: орт X, орт Y, орт Z.
• Орты базиса пространства: орт i, орт j, орт k.
• Орты физических величин: орт силы, орт скорости, орт магнитного поля.

Орт в трехмерном пространстве: специфика и примеры

Орт можно представить с помощью его координат. Вектор орта имеет длину равную 1 и обозначается символом i, j или k, в зависимости от осей координат X, Y или Z соответственно.

Примеры ортов в трехмерном пространстве:

1. Орт i: (1, 0, 0) — этот орт указывает в положительном направлении оси X.

2. Орт j: (0, 1, 0) — этот орт указывает в положительном направлении оси Y.

3. Орт k: (0, 0, 1) — этот орт указывает в положительном направлении оси Z.

Орты в трехмерном пространстве используются во многих областях, таких как геометрия, физика, компьютерная графика и другие. Они позволяют определить направление и углы между векторами, а также проводить различные вычисления и преобразования.

Ортогональность векторов: условия и свойства

a ⋅ b = 0

Условие ортогональности можно использовать для определения и проверки различных свойств векторов. Некоторые из этих свойств включают:

1. Ортогональность нулевого вектора. Нулевой вектор ортогонален любому другому вектору, так как его скалярное произведение с любым вектором равно нулю.

2. Ортогональность скалярного произведения себя же. Скалярное произведение вектора на самого себя равно квадрату его длины. Если скалярное произведение равно нулю, то длина вектора также равна нулю.

3. Ортогональность векторов в ортогональном базисе. Векторы, составляющие ортогональный базис векторного пространства, являются попарно ортогональными. Скалярное произведение любых двух векторов из этого базиса равно нулю.

4. Ортогональность суммы векторов и их разности. Если векторы a и b ортогональны, то их сумма a + b и разность a — b также будут ортогональны.

Ортогональность векторов имеет широкое применение в геометрии, физике и других областях науки. Она позволяет решать множество задач, связанных с анализом и манипуляциями векторами.

Ортонормированный базис: определение и применение

Ортонормированный базис имеет важное применение в математике, физике и других областях. Он позволяет удобно описывать и анализировать различные объекты и явления. Например, вектора в ортонормированном базисе удобно использовать для разложения векторов на компоненты или для нахождения коэффициентов разложения векторов в линейной комбинации.

Ортонормированный базис также является основой для работы с матрицами и операторами. Матрицы, заданные в ортонормированном базисе, имеют определенные свойства, которые упрощают их анализ и применение. Операторы, заданные в ортонормированном базисе, обладают особыми свойствами, например, они могут быть диагонализированы.

Примеры ортонормированных базисовПрименение

Канонический базис (1, 0, 0), (0, 1, 0), (0, 0, 1)	Описание пространственных координат в трехмерном пространстве
Базис Фурье	Разложение функций на гармонические компоненты
Ортонормированный базис собственных векторов	Диагонализация матриц и решение систем линейных дифференциальных уравнений

Ортонормированный базис является важным инструментом в математике и физике, который позволяет удобно и эффективно работать с векторами, матрицами и операторами. Понимание его определения и применения является основой для дальнейшего изучения различных разделов математики и физики.

Матрица ортогонального преобразования: структура и свойства

Структура матрицы ортогонального преобразования имеет следующий вид:

Матрица A является матрицей ортогонального преобразования, если выполняется условие:

AT * A = I,

где AT — транспонированная матрица A, I — единичная матрица.

То есть, произведение матрицы A на транспонированную матрицу A должно быть равно единичной матрице. Это условие гарантирует, что матрица A сохраняет длины векторов и углы между ними.

Свойства матрицы ортогонального преобразования:

1. Определитель матрицы ортогонального преобразования равен 1 или -1. Это следует из свойств определителя и условия AT * A = I. Если определитель равен 1, матрица A называется ортогональной. Если определитель равен -1, матрица A называется антиортогональной.

2. Обратная матрица к ортогональной матрице также является ортогональной.

3. Произведение двух ортогональных матриц также является ортогональной матрицей.

4. Ортогональное преобразование сохраняет скалярное произведение двух векторов. Для произвольных векторов x и y выполняется условие (Ax)T * (Ay) = xT * y.

Примеры матриц ортогонального преобразования:

1. Матрица поворота на угол α в двумерном пространстве:

[[cos(α), -sin(α)],

[sin(α), cos(α)]].

Эта матрица поворачивает векторы на угол α против часовой стрелки.

2. Матрица отражения относительно прямой с заданным направляющим вектором:

[[cos(α), sin(α)],

[sin(α), -cos(α)]].

Эта матрица отражает векторы относительно прямой с заданным направляющим вектором.

Матрица ортогонального преобразования имеет важное значение в линейной алгебре и может быть использована для решения различных задач, связанных с преобразованием и анализом векторов.

Ортогональные группы и их представление

Ортогональные группы, обозначаемые как O(n), представляют собой группы линейных преобразований n-мерного евклидова пространства, которые сохраняют скалярное произведение. Это означает, что для любых двух векторов u и v в евклидовом пространстве, их скалярное произведение остается неизменным после применения линейного преобразования из группы O(n).

Ортогональные группы имеют множество свойств и характеристик, которые делают их особенно полезными в различных приложениях. Они обладают замкнутостью относительно композиции преобразований, что позволяет эффективно комбинировать операции. Они также сохраняют длину векторов и углы между ними, что делает их подходящими для решения задач, связанных с геометрией и физикой. Кроме того, ортогональные группы имеют связь с симметриями и симметричными матрицами.

Представление ортогональных групп играет важную роль в теории представлений, которая изучает разложение группы на неприводимые подгруппы. Оно позволяет анализировать структуру ортогональных групп и связанные с ними математические объекты. Представление ортогональных групп часто находит применение в физике, в том числе в квантовой механике и статистической механике, где они используются для описания симметричных систем и фазовых переходов.

В заключение, ортогональные группы и их представление играют важную роль в различных областях математики и ее приложениях. Изучение и анализ этих групп позволяет получить глубокое понимание симметрии и структуры математических объектов, а также разрабатывать эффективные алгоритмы и методы решения задач.

Ортогональные проекции: применение и свойства

Проекция осуществляется путем перпендикулярного опускания точки или фигуры на плоскость. При этом проекция вектора на плоскость называется ортогональной проекцией.

Ортогональные проекции обладают рядом свойств:

1. Ортогональная проекция вектора на плоскость является вектором, коллинеарным с самим вектором.

2. Проекция вектора на плоскость имеет меньшую или равную длину, чем сам вектор.

3. Если два вектора ортогональны, то их проекции на одну и ту же плоскость также будут ортогональны.

Ортогональные проекции находят применение в различных задачах. Например, в графике они используются для создания трехмерных изображений на двухмерной плоскости. В архитектуре ортогональные проекции позволяют строить планы зданий и конструкций. В физике они используются для анализа движения тел и расчетов силы удара.

В заключение, ортогональные проекции являются важным инструментом в геометрии и находят широкое применение в различных областях. Их свойства позволяют упростить анализ и решение задач, связанных с проекцией объектов на плоскость.

Вопрос-ответ:

Что такое орт в математике?

Орт в математике — это вектор единичной длины, ортогональный (перпендикулярный) к другому вектору или плоскости.

Как можно определить орт?

Орт можно определить с помощью некоторых свойств. Вектор является ортом, если его длина равна 1 и он ортогонален (перпендикулярен) к другому вектору или плоскости.

Какие свойства имеют орты?

Орты имеют несколько свойств. Во-первых, они являются единичными векторами, то есть их длина равна 1. Во-вторых, орты ортогональны другим векторам или плоскостям. В-третьих, они могут использоваться для разложения других векторов на компоненты.

Какие примеры ортов можно привести?

Примерами ортов могут служить единичные векторы, направленные вдоль осей координат: i, j, k. Они ортогональны другим осям и образуют базис пространства.

Зачем нужны орты в математике?

Орты в математике играют важную роль. Они помогают разложить векторы на компоненты, что позволяет упростить решение задач и работу с векторами. Орты также используются в различных областях науки и инженерии, включая физику, компьютерную графику и машинное обучение.

Орт в комплексных числах: особенности и примеры

Основное свойство орта в комплексных числах заключается в том, что его четвёртая степень равна единице:

i4 = 1

Здесь i — мнимая единица, определяемая следующим образом:

i = √(-1)

Комплексные числа представляются в виде a + bi, где a и b — действительные числа, а i — мнимая единица. Орт в комплексных числах можно представить в виде:

i = cos(π/2) + i·sin(π/2)

Орт также имеет геометрическую интерпретацию. Он является точкой на комплексной плоскости, находящейся на расстоянии 1 от начала координат и образующей угол π/2 с положительным направлением оси X.

Примеры использования орта в комплексных числах включают решение уравнений, математические моделирования и применение в физике. Орт также используется для представления поворотов и масштабирования в двумерной геометрии.

Видео по теме: