Основная цель математической статистики: что она изучает и зачем это важно

Основная цель математической статистики заключается в анализе данных и получении информации о вероятностных свойствах и закономерностях распределения случайных величин в различных областях науки и практики. Результаты этого анализа помогают принимать взвешенные решения и оптимизировать процессы в различных сферах деятельности.

Математическая статистика – это раздел математики, который изучает методы анализа данных и дает возможность получать выводы на основе вероятностных закономерностей. В основе математической статистики лежит использование теории вероятностей, позволяющей описывать реальные явления в терминах их вероятностных характеристик. Цель математической статистики – изучение этих вероятностных закономерностей и построение моделей, описывающих их поведение.

Одной из основных задач математической статистики является оценка параметров статистических моделей, на основе которых делаются различные выводы. Также математическая статистика охватывает важную область – теорию проверки гипотез. Это позволяет исследователям делать выводы о вероятных свойствах данных, а также сравнивать данные между собой и выявлять существенные различия.

Математическая статистика является необходимым инструментом в различных областях знания, от физики и биологии до экономики и социологии. Она также играет важную роль в различных бизнес-приложениях, позволяя проводить анализ рынка, выявлять тенденции развития отраслей и делать прогнозы на будущее.

Что такое математическая статистика?

Математическая статистика — это раздел математики, который изучает методы анализа случайных явлений. В частности, математическая статистика помогает изучить вероятностные закономерности в данных, полученных в ходе экспериментов и наблюдений.

Задача математической статистики — найти закономерности в данных и описать их путем построения вероятностных моделей. Например, математическая статистика может помочь определить, какие действия следует предпринимать для увеличения прибыли на основе анализа данных о продажах.

Математическая статистика используется во многих областях, включая физику, экономику, биологию и медицину. Например, математическая статистика может использоваться для изучения взаимосвязи между факторами риска и заболеваниями или для анализа экономических данных для предсказания будущих трендов и принятия бизнес-решений.

Основные методы математической статистики включают в себя описательную статистику, инференциальную статистику и регрессионный анализ. Кроме того, математическая статистика использует различные статистические модели, такие как нормальное распределение, регрессионная модель и анализ дисперсии.

В целом, математическая статистика помогает ученым и исследователям находить закономерности в данных и принимать более обоснованные решения на основе этих данных. Таким образом, математическая статистика является очень важным инструментом в современном мире.

Видео по теме:

Зачем изучать вероятностные закономерности в данных?

Одна из главных задач математической статистики – это изучение вероятностных закономерностей в данных. Зачем это нужно?

Во-первых, понимание вероятностных закономерностей позволяет определить, насколько случайна та или иная выборка данных. Изучение вероятностных закономерностей помогает проводить статистические испытания, которые позволяют сделать выводы о значимости или незначимости результата.

Во-вторых, знание вероятностных закономерностей позволяет оценить параметры распределения, на основе которого получены данные. Например, это может быть среднее значение, стандартное отклонение, корреляционный коэффициент и другие. Это в свою очередь позволяет построить модель, которая описывает данные наилучшим образом.

В-третьих, изучение вероятностных закономерностей в данных помогает исследовать зависимости между различными переменными, обрабатывать и анализировать информацию, прогнозировать будущие события и принимать решения на основе статистических данных.

В целом, изучение вероятностных закономерностей в данных является необходимым шагом для получения какого-либо осмысленного вывода по данным. Статистика играет ключевую роль в обработке и анализе данных, а знание вероятностных закономерностей позволяет ее применять эффективно и достоверно.

Статистические методы и их применение

Математическая статистика предлагает широкий спектр статистических методов, которые могут быть применены к данным, чтобы изучать вероятностные закономерности. Чаще всего используются следующие методы:

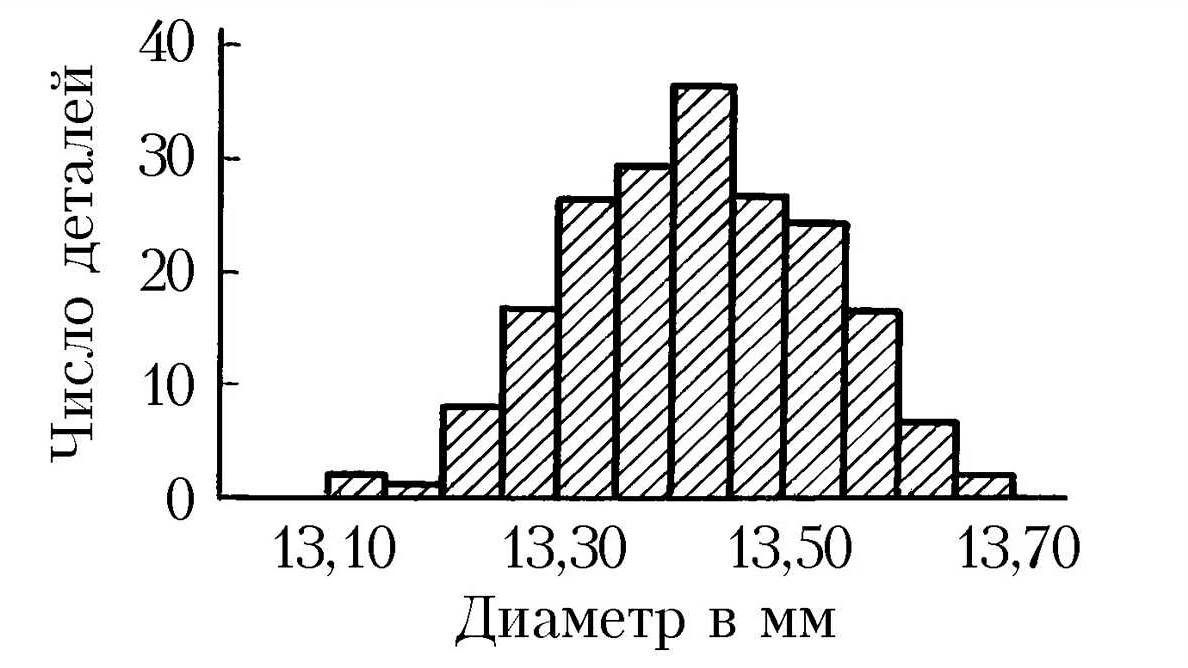
• Описательная статистика — методы сбора, описания, визуализации и интерпретации данных. Они включают в себя распределения, гистограммы, диаграммы рассеяния и многое другое. Эти методы помогают понять, как распределяется данные по различным параметрам.
• Инференциальная статистика — методы, которые позволяют сделать выводы о генеральной совокупности на основе выборочных данных. Эти методы включают в себя гипотезы, тесты, интервалы доверия и регрессионный анализ.
• Регрессионный анализ — метод, который позволяет исследовать связь между независимыми и зависимыми переменными. Он часто используется для прогнозирования будущих значений на основе прошлых данных.
• Машинное обучение — также постепенно начинает проникать в область математической статистики и включает в себя методы, такие как классификация и кластеризация данных.

Каждый из этих методов имеет свои преимущества и недостатки, и выбор подходящего метода зависит от нашей цели и типа данных, которые мы изучаем. В некоторых случаях мы можем использовать несколько методов, чтобы получить более точные и надежные результаты.

Статистические методы могут быть применены в различных областях, таких как медицина, экономика, социология, бизнес и инженерия. Они используются для исследования различных аспектов, например, для проверки эффективности лекарств, прогнозирования будущих продаж, определения оптимального размера производства и т. д.

Использование статистических методов может помочь нам принимать более обоснованные и грамотные решения, основанные на данных. Статистические методы дают нам возможность извлекать информацию из сложных наборов данных и сделать выводы на основе этой информации.

Вероятностные распределения и их использование

Ключевым инструментом математической статистики являются вероятностные распределения. Вероятностное распределение описывает вероятности всех возможных значений случайной величины (например, время выполнения задачи, выигрыш в лотерее, уровень дохода и т.п.).

Вероятностные распределения являются не только инструментом для описания статистических данных, но и позволяют проводить различные статистические тесты, анализировать и предсказывать результаты исследований, использовать в машинном обучении и прогнозировании.

Наиболее распространенным вероятностным распределением является нормальное (Гауссово) распределение, которое описывает большинство случайных величин в природе и обществе. Оно широко используется в статистических моделях и эконометрике.

Кроме того, есть множество других вероятностных распределений, таких как биномиальное, Пуассоновское, экспоненциальное, гамма-распределение и многие другие. Каждое из них используется для описания конкретных типов данных и имеет свои характеристики и применения.

1. Биномиальное распределение — используется для описания двоичных данных, таких как количество успехов или неудач в серии независимых испытаний
2. Пуассоновское распределение — используется для описания счетных данных, таких как количество звонков в колл-центре за определенный период времени
3. Экспоненциальное распределение — используется для описания времени до наступления события, например, время между отказами в работе оборудования

Использование правильного вероятностного распределения является ключевым для корректной интерпретации и анализа статистических данных и предсказания будущих значений. Поэтому понимание основных типов вероятностных распределений является важным навыком для специалистов в области математической статистики и анализа данных.

Оценка и интерпретация статистических данных

Основная цель математической статистики заключается в изучении вероятностных закономерностей в данных. При этом одним из наиболее важных этапов является оценка и интерпретация статистических данных. Данные могут быть получены в результате опросов, экспериментов или наблюдений, и их анализ может привести к выявлению закономерностей и связей.

Оценка данных включает в себя различные методы, такие как описательная статистика, корреляционный анализ и регрессионный анализ. Описательная статистика используется для выражения данных в форме числовых значений, таких как среднее значение, медиана, дисперсия и стандартное отклонение.

Корреляционный анализ используется для изучения связей между двумя или более переменными, а регрессионный анализ позволяет идентифицировать зависимости между двумя переменными, определяя одну как зависимую, а другую как независимую.

Интерпретация статистических данных заключается в том, чтобы получить понимание о том, как различные факторы могут влиять на результаты. Это может включать в себя анализ выборочных характеристик, таких как вероятность, доверительный интервал и статистическую значимость, чтобы понять, насколько можно доверять полученным результатам.

В целом, оценка и интерпретация статистических данных являются важным процессом в науке, экономике, медицине и других областях, где нужно анализировать и понимать данные в целях получения новых знаний и принятия решений.

Важность выборки в математической статистике

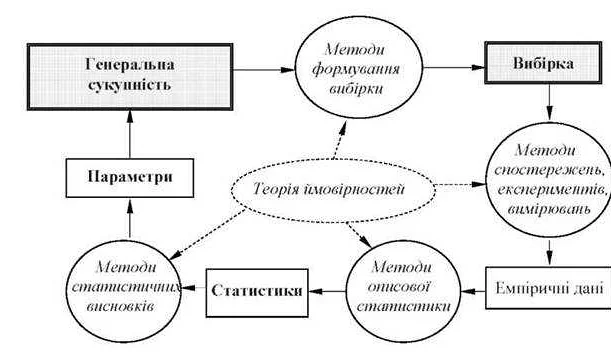
Выборка – это случайная подвыборка из генеральной совокупности, из которой проводится исследование. Определение вероятностей для генеральной совокупности обычно является нереальным, поэтому мы анализируем выборку или несколько выборок, с целью определенного вывода на основе вероятностных закономерностей в данных.

Основная цель выборки – изучение структуры данных, которые представлены в выборке, и установление зависимостей между различными факторами. Важно, чтобы выборка наилучшим образом представляла генеральную совокупность и обеспечивала статистическую значимость результатов. В противном случае результаты будут непредставительными и ошибочными.

Размер выборки – один из основных факторов, который может повлиять на результаты исследования. Чем больше размер выборки, тем выше уровень достоверности результатов. Однако, слишком большой размер выборки может быть излишним и неэффективным, особенно если данные имеют сложную структуру или содержат выбросы.

Выборочная средняя и стандартное отклонение – две основные характеристики выборки, которые используются для анализа данных в математической статистике. Выборочная средняя – среднее значение числовых данных в выборке, а стандартное отклонение – мера разброса данных вокруг среднего значения. Эти характеристики можно использовать для оценки основных характеристик генеральной совокупности.

Вывод: выборка является фундаментальным инструментом математической статистики, используемым для анализа данных, изучения закономерностей в данных и установления статистической значимости результатов. Важно выбирать наиболее представительные выборки с оптимальным размером, и использовать основные характеристики, такие как выборочная средняя и стандартное отклонение, для обработки данных и оценки характеристик генеральной совокупности.

Проверка гипотез в математической статистике

Одной из основных задач математической статистики является проверка гипотез о параметрах распределения случайной величины по имеющимся статистическим данным. Например, мы можем проверять гипотезы о равенстве средних значений двух выборок, о нормальности распределения выборки и т.д.

Для проведения проверки гипотез в математической статистике используются статистические критерии. Суть критерия заключается в определении вероятности получения таких или еще более крайних значений статистической величины, если гипотеза верна. На основе этой вероятности принимается решение о том, отвергается или не отвергается гипотеза.

Для принятия решения о принятии или отвержении гипотезы в математической статистике используются уровни значимости. Уровень значимости — это фиксированная вероятность ошибочно отвергнуть верную гипотезу. Обычно уровень значимости равен 0,05 или 0,01.

При проверке гипотез в математической статистике могут быть допущены два вида ошибок: ошибка первого рода — отвержение верной гипотезы и ошибка второго рода — принятие не верной гипотезы. Ошибка первого рода считается более серьезной, поэтому уровень значимости обычно выбирают таким, чтобы вероятность ошибки первого рода была минимальной.

Важность проверки гипотез в математической статистике заключается в том, что она позволяет научно исследовать и объяснить закономерности, скрытые в статистических данных. Кроме того, проверка гипотез позволяет сделать выводы о популяции на основе данных, полученных из выборок.

Регрессионный анализ и его роль в математической статистике

Регрессионный анализ – один из наиболее важных инструментов математической статистики, который позволяет определить математическую зависимость между двумя и более переменными. При этом одна переменная выступает в качестве зависимой, а другие – в качестве независимых.

Регрессионный анализ основывается на регрессионной модели, которая может быть представлена в виде уравнения. Если уравнение модели имеет линейную форму, то она называется линейной регрессионной моделью.

Линейная регрессионная модель является наиболее распространенной и широко используется в различных областях, включая экономику, социологию, биологию и физику. Она позволяет определить, какое изменение в независимой переменной будет соответствовать изменению в зависимой переменной.

Одной из самых распространенных и важных задач регрессионного анализа является прогнозирование. Регрессионная модель может использоваться для прогнозирования значений зависимой переменной на основе известных значений независимых переменных. Это очень важно в бизнесе и экономике и помогает предугадать, как изменение одной переменной повлияет на другие в будущем.

В целом, регрессионный анализ играет важную роль в математической статистике, предоставляя инструменты для анализа и понимания данных. Он используется для выявления закономерностей в данных и прогнозирования будущих значений. Благодаря этому, регрессионный анализ является признанным инструментом во многих областях и оказывает значительное влияние на принятие решений в различных организациях и индустриях.

Применение математической статистики в реальной жизни

Математическая статистика находит свое применение во многих областях жизни, от экономики и финансов до медицины и науки о климате. Например, в экономических и финансовых исследованиях математические статистические методы могут помочь определить экономические тенденции, оценить риски и принимать решения на основе реальных данных.

В медицине математическая статистика используется для анализа статистических данных о заболеваемости, распространении болезней, проведения клинических испытаний и т.д. Эти данные могут помочь улучшить диагностику и лечение заболеваний.

Наука о климате также обращается к математической статистике для анализа и моделирования климатических изменений на основе статистических данных. Это может помочь в прогнозировании будущих изменений климата и разработке стратегий для защиты окружающей среды.

В области бизнеса математическая статистика может быть применена для анализа данных о потребителях, рынках, продажах и т.д. Эта информация может быть полезна для разработки маркетинговых стратегий и улучшения продуктов и услуг.

Сегодня математическая статистика особенно важна в контексте цифровой революции, так как объемы данных, генерируемых в различных сферах, постоянно растут. Применение методов математической статистики помогает организациям извлечь ценную информацию из данных и сформулировать более эффективные и точные стратегии для достижения своих целей.

Вопрос-ответ:

Какая основная цель математической статистики?

Основная цель математической статистики — изучение вероятностных закономерностей в данных, объяснение их природы и использование полученных знаний для прогнозирования будущих событий.

Что такое вероятностные закономерности в данных?

Вероятностные закономерности в данных — это законы, которые описывают вероятность того, что определенное событие произойдет в будущем на основе статистических данных прошлого.

Как математическая статистика помогает в прогнозировании будущих событий?

Математическая статистика позволяет анализировать данные, предсказывать будущие тенденции и принимать решения на основе вероятностных моделей.

Какие методы используются в математической статистике для изучения данных?

В математической статистике используются методы описательной и инференциальной статистики, регрессионного анализа, анализа временных рядов, анализа факторов и другие методы для различных типов данных.

Какие области знаний используют математическую статистику?

Математическая статистика находит применение во многих областях знаний, включая экономику, физику, химию, медицину, биологию, социологию и другие.

Какие проблемы могут возникнуть при анализе больших объемов данных при помощи математической статистики?

При анализе больших объемов данных возникают проблемы с вычислительной сложностью, а также проблемы с выбором статистических методов. Важно также правильно интерпретировать полученные результаты и не делать ошибок в выводах.

Какие навыки необходимы для работы с математической статистикой?

Для работы с математической статистикой необходимы навыки работы с программным обеспечением, статистические знания, математические знания, умение анализировать результаты и делать выводы на основе данных.