Что из перечисленного выступает математической основой статистических закономерностей

Читайте статью и узнайте, какие из перечисленных элементов являются математической основой для статистических закономерностей. Узнайте, как математика помогает нам понять и анализировать данные и выявлять закономерности в статистике.

Статистические закономерности играют важную роль в различных областях науки, от экономики и социологии до физики и биологии. Они позволяют нам понять и описать различные явления, происходящие в окружающем нас мире. Однако, в основе этих закономерностей лежит математическая теория, которая позволяет нам анализировать данные и делать выводы на основе вероятностных моделей.

Одним из ключевых понятий в математической статистике является вероятность. Вероятность определяет, насколько вероятно возникновение какого-либо события. Она позволяет нам оценить, насколько надежными являются наши данные и какие выводы можно сделать на основе этих данных. Вероятность также позволяет нам определить степень уверенности в наших результатах и построить доверительные интервалы для оценки параметров.

Еще одним важным понятием является случайная величина. Случайная величина описывает значения, которые могут принимать определенные события или явления. Она позволяет нам моделировать и анализировать случайные процессы и предсказывать вероятности различных исходов. На основе случайной величины мы можем строить различные статистические модели и делать выводы о распределении данных.

Однако, без математической основы все эти понятия и методы не могут быть полноценно применены. Математические модели и теории позволяют нам формализовать наши предположения и проверять их на основе собранных данных. Они также позволяют нам разрабатывать новые методы анализа данных и улучшать существующие.

Таким образом, математическая основа статистических закономерностей является ключевым элементом для понимания и анализа данных. Она позволяет нам строить модели, предсказывать вероятности и делать выводы на основе собранных данных. Без нее, статистические закономерности были бы лишь набором наблюдений без понятной закономерности.

Математическая основа статистических закономерностей: ключевые аспекты

Одним из ключевых аспектов математической основы статистических закономерностей является теория вероятностей. Теория вероятностей позволяет формализовать случайные явления и описывать их с помощью математических моделей. Вероятность события определяется как число, отражающее степень его возможности.

Другим важным аспектом является математическая статистика. Математическая статистика позволяет извлекать информацию из данных, проводить их анализ и делать выводы о генеральной совокупности на основе выборочных данных. Она включает в себя методы описательной статистики, которые позволяют описывать и анализировать данные, и методы индуктивной статистики, которые позволяют делать выводы на основе выборочных данных.

Еще одним ключевым аспектом является теория случайных процессов. Теория случайных процессов изучает эволюцию случайных величин во времени. Она позволяет анализировать случайные процессы, такие как случайные блуждания, случайные графы и другие объекты.

Таким образом, математическая основа статистических закономерностей включает в себя теорию вероятностей, математическую статистику и теорию случайных процессов. Эти аспекты позволяют формализовать и анализировать статистические данные, понимать закономерности в случайных явлениях и делать выводы на основе выборочных данных.

Вероятность и статистика: взаимосвязь и различия

• Вероятность — это математическое понятие, которое изучает возможные исходы событий и их вероятности. Вероятность используется для моделирования случайных явлений и предсказания вероятности определенных исходов. Она основывается на математических законах и формулах, таких как формула вероятности или теорема Байеса.
• Статистика — это наука, которая изучает сбор, анализ и интерпретацию данных для принятия выводов и прогнозов о популяции. Статистика используется для извлечения информации и закономерностей из данных, а также для проверки гипотез и принятия решений на основе полученных результатов.

Таким образом, вероятность и статистика имеют общую цель — понимание и объяснение случайных явлений. Однако, вероятность фокусируется на предсказании вероятности исходов, основываясь на математических моделях, а статистика использует данные и методы анализа для извлечения информации о популяции и принятия выводов.

Взаимосвязь между вероятностью и статистикой заключается в том, что статистические методы могут использовать вероятностные модели для анализа данных и извлечения статистических закономерностей. Например, методы регрессии и корреляции используют вероятностные модели для объяснения связей между переменными.

Однако, различия между вероятностью и статистикой также очевидны. Вероятность фокусируется на предсказании вероятностей исходов, основываясь на математических законах, в то время как статистика фокусируется на анализе данных и извлечении информации о популяции. Кроме того, статистика может использовать различные методы и подходы для анализа данных, включая методы случайной выборки, максимального правдоподобия и байесовский подход.

Таким образом, вероятность и статистика являются взаимосвязанными понятиями, которые имеют сходства и различия в своих подходах и методах. Понимание и использование обоих понятий позволяет получить полное представление о случайных явлениях и их закономерностях.

Случайные величины и распределения: основные понятия

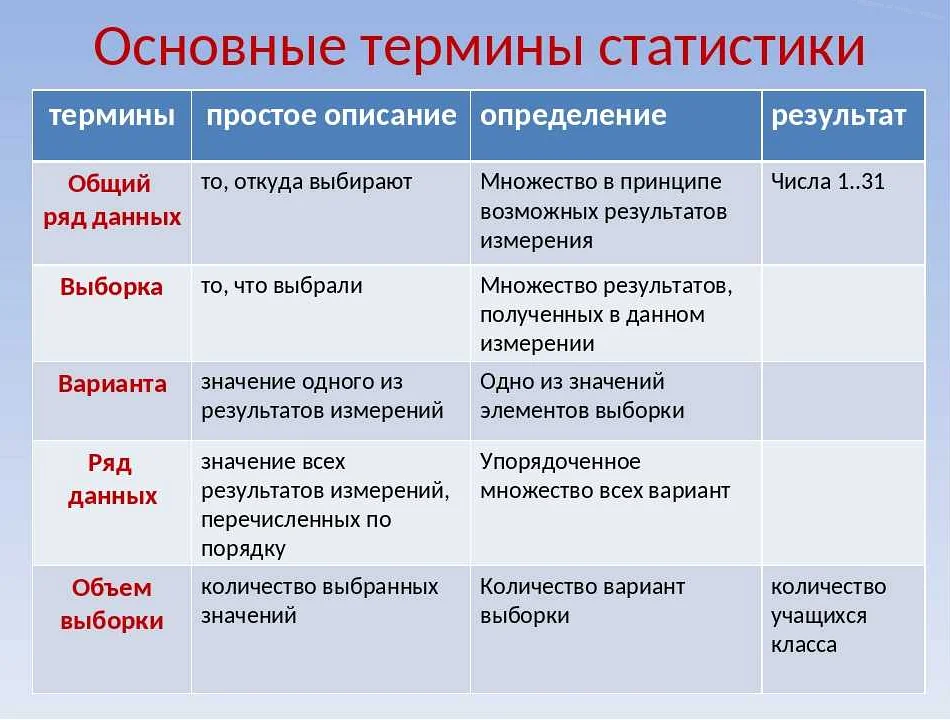
Случайная величина представляет собой функцию, которая ставит в соответствие каждому элементу выборки числовое значение. Она может принимать различные значения в зависимости от исхода случайного эксперимента.

Случайные величины делятся на два типа: дискретные и непрерывные. Дискретные случайные величины принимают только конкретные значения из некоторого множества, например, количество выпавших орлов при подбрасывании монеты. Непрерывные случайные величины могут принимать любое значение в некотором интервале, например, время, которое требуется для прохождения определенного расстояния.

Для характеристики случайных величин используются различные распределения. Распределение случайной величины описывает вероятность того, что она примет определенное значение или попадет в определенный интервал. Наиболее известные распределения — это равномерное, нормальное и пуассоновское распределения.

РаспределениеОписание

Равномерное	Все значения случайной величины имеют одинаковую вероятность
Нормальное	Значения случайной величины сгруппированы вокруг среднего значения
Пуассоновское	Используется для моделирования счетных данных, таких как число событий в определенном временном интервале

Знание основных понятий случайных величин и распределений является важной составляющей математической статистики. Оно позволяет проводить анализ данных, прогнозировать вероятности и принимать обоснованные решения на основе статистических закономерностей.

Центральная предельная теорема: ключевая роль в статистике

Центральная предельная теорема утверждает, что сумма большого числа независимых и одинаково распределенных случайных величин приближается к нормальному распределению независимо от исходного распределения этих случайных величин. Это означает, что даже если исходное распределение не является нормальным, сумма большого числа случайных величин будет иметь распределение, близкое к нормальному.

Центральная предельная теорема имеет важное практическое применение в статистике. Она позволяет использовать нормальное распределение для оценки вероятностей и построения доверительных интервалов для различных статистических характеристик, таких как среднее значение или сумма случайных величин. Благодаря этой теореме можно делать выводы о генеральной совокупности на основе выборочных данных, даже если генеральная совокупность имеет неизвестное или сложное распределение.

Центральная предельная теорема также позволяет определить, насколько выборочное среднее или другая статистическая характеристика отличается от среднего значения в генеральной совокупности. Это основа для проведения гипотезных тестов и статистического вывода.

Таким образом, центральная предельная теорема играет ключевую роль в статистике, обеспечивая математическую основу для статистических закономерностей и позволяя делать выводы о генеральной совокупности на основе выборочных данных.

Закон больших чисел: суть и применение

Суть закона больших чисел заключается в том, что при проведении достаточно большого числа независимых экспериментов результаты средних значений будут стремиться к теоретическим значениям. Это означает, что при большом объеме данных статистические характеристики, такие как среднее значение, будут очень близки к значениям, которые можно было бы получить, если бы все возможные эксперименты были проведены.

Закон больших чисел находит применение в различных областях, в том числе в финансовой аналитике, демографии, экономике и физике. Например, он используется для оценки вероятности исходов в случайных процессах, для прогнозирования будущих значений случайных величин и для определения статистической значимости результатов исследований.

Закон больших чисел позволяет улучшить точность статистических выводов и прогнозов на основе больших объемов данных. Он является основой для многих статистических методов и моделей и существенно влияет на развитие и применение статистики в различных областях науки и практики.

Параметрические и непараметрические методы статистики

Параметрические методы статистики основаны на предположении о распределении данных в генеральной совокупности. Они требуют установления параметров, таких как среднее значение и дисперсия, и предполагают, что данные распределены по определенному закону, такому как нормальное распределение. Примерами параметрических методов являются t-тест, анализ дисперсии и линейная регрессия.

Непараметрические методы статистики не требуют определения параметров распределения данных и не предполагают никаких предположений о его форме. Вместо этого они основываются на ранжировании данных и использовании непараметрических статистик, таких как медиана, ранговый коэффициент корреляции и критерий знаков. Непараметрические методы часто используются, когда данные не соответствуют предположениям о нормальном распределении или когда объем выборки слишком мал. Примерами непараметрических методов являются критерий Манна-Уитни, критерий Вилкоксона и тест Колмогорова-Смирнова.

Выбор между параметрическими и непараметрическими методами статистики зависит от характера данных и цели исследования. Параметрические методы обычно более мощные и дают более точные результаты, если предположения о распределении данных соблюдаются. Непараметрические методы являются более гибкими и робастными в отношении предположений о распределении данных, но могут требовать большего объема данных для достижения статистической значимости.

Проверка статистических гипотез: основные подходы

Основными подходами к проверке статистических гипотез являются:

1. Параметрический подход. В рамках параметрического подхода предполагается, что исследуемая выборка имеет определенное вероятностное распределение (например, нормальное распределение). Для проверки гипотез используются статистические критерии, такие как t-критерий Стьюдента, анализ дисперсии и другие.
2. Непараметрический подход. В отличие от параметрического подхода, непараметрический подход не требует предположения о распределении выборки. Вместо этого используются ранги или другие не параметрические статистические методы. Наиболее известные непараметрические критерии включают ранговый критерий Уилкоксона-Манна-Уитни, критерий знаков и другие.
3. Байесовский подход. Байесовский подход основан на принципах байесовской статистики и позволяет оценивать вероятности гипотез на основе априорной информации и данных. Для проверки гипотез в рамках байесовского подхода используются байесовские факторы и другие байесовские методы.

Выбор подхода к проверке статистических гипотез зависит от характера данных, целей исследования и предположений, сделанных о распределении выборки. Каждый из подходов имеет свои преимущества и ограничения, поэтому важно выбрать подход, наиболее подходящий для конкретной задачи.

Видео по теме:

Вопрос-ответ:

Какие математические законы лежат в основе статистических закономерностей?

Математические законы, лежащие в основе статистических закономерностей, включают в себя законы вероятности, теорию множеств, теорию функций и др.

Почему математическая основа статистических закономерностей является ключевой?

Математическая основа статистических закономерностей является ключевой, так как она позволяет проводить точные и надежные статистические исследования, а также делать прогнозы и принимать взвешенные решения на основе полученных данных.

Какие применения имеет математическая основа статистических закономерностей?

Математическая основа статистических закономерностей имеет множество применений, включая анализ рынка, прогнозирование погоды, определение рисков и вероятностей, моделирование физических и социальных процессов и многое другое.

Какие конкретные математические методы используются для анализа статистических закономерностей?

Для анализа статистических закономерностей используются такие математические методы, как математическая статистика, теория вероятностей, линейная алгебра, математическая логика и др.

Как математическая основа статистических закономерностей помогает в принятии решений в бизнесе?

Математическая основа статистических закономерностей помогает в бизнесе принимать обоснованные и обосновываемые решения на основе анализа данных, определения вероятностей и рисков, моделирования процессов и т.д. Это позволяет снизить неопределенность и повысить эффективность принимаемых решений.

Какая математическая основа лежит в основе статистических закономерностей?

Математическая основа статистических закономерностей заключается в применении вероятностных методов и моделей для анализа и описания случайных явлений.

Почему вероятностные методы являются ключевой математической основой статистических закономерностей?

Вероятностные методы позволяют описывать случайные явления и предсказывать их вероятность. Они позволяют осуществлять статистический анализ данных и находить закономерности в больших объемах информации.

Регрессионный анализ: прогнозирование на основе данных

В основе регрессионного анализа лежит концепция линейной регрессии, которая предполагает, что связь между независимыми и зависимой переменными может быть описана линейной функцией. Однако, регрессионный анализ также может использовать и другие типы регрессии, такие как полиномиальная, экспоненциальная или логарифмическая регрессия, в зависимости от природы данных и характера связи.

Прогнозирование на основе данных — это одна из основных задач регрессионного анализа. При помощи построенной модели регрессии можно предсказать значения зависимой переменной для новых наблюдений, основываясь на значениях независимых переменных. Это позволяет делать прогнозы и принимать решения на основе имеющихся данных, что является важным инструментом во многих областях, таких как экономика, финансы, маркетинг и т.д.

Для успешного применения регрессионного анализа и прогнозирования на основе данных необходимо учитывать ряд факторов. Во-первых, выбор независимых переменных должен быть обоснованным и основываться на теоретических предположениях или экономической логике. Во-вторых, необходимо учитывать качество данных и их статистические свойства, такие как нормальность распределения и отсутствие мультиколлинеарности. Кроме того, важно провести анализ остатков и проверить адекватность построенной модели.

В итоге, регрессионный анализ и прогнозирование на основе данных являются мощными инструментами статистического анализа, которые позволяют получать ценные знания и делать прогнозы на основе имеющихся данных. Однако, для успешного применения этих методов необходимо учесть ряд факторов и особенностей данных.

Интервальная оценка и доверительные интервалы: точность измерений

Интервальная оценка основана на том, что выборочные данные представляют собой только часть всей генеральной совокупности. Применение интервальной оценки позволяет сделать вывод о параметрах генеральной совокупности на основе доступной выборки.

Доверительный интервал – это интервал, который с определенной вероятностью содержит истинное значение параметра генеральной совокупности. Например, если мы вычислили доверительный интервал для среднего значения, то это означает, что с заданной вероятностью истинное среднее значение находится в данном интервале.

Точность измерений, оцененная с помощью интервальной оценки и доверительных интервалов, зависит от размера выборки, уровня доверия и дисперсии генеральной совокупности. Чем больше выборка и чем более узкий интервал, тем меньше возможность ошибки при оценке параметра.

Использование интервальной оценки и доверительных интервалов позволяет более точно оценить параметры генеральной совокупности и принять обоснованные выводы на основе имеющихся данных.