Что составляет основу содержания начального курса математики
Содержимое
- 1 Что составляет основу содержания начального курса математики
Основа содержания начального курса математики включает основные математические понятия и навыки, такие как арифметика, геометрия, измерения, статистика и вероятность. В этой статье вы узнаете, какие темы и концепции входят в начальный курс математики и как они помогают развивать математическое мышление у детей.
Начальный курс математики является одним из основных компонентов образования и представляет собой важную часть базового образования. Он знакомит учеников с основными понятиями и способами работы в математике. Начальная школа знакомит детей с числами, арифметическими операциями, геометрией, измерением, анализом данных и другими ключевыми темами, которые являются фундаментом для дальнейшего изучения математики.
Одной из основных тем начального курса математики является изучение чисел и арифметики. Ученики учатся считать, складывать, вычитать, умножать и делить числа. Они также изучают различные свойства чисел, такие как четность и нечетность, простые и составные числа, десятичные дроби и дробные числа.
Еще одной важной темой является геометрия. Ученики учатся определять и называть различные геометрические фигуры, такие как круг, квадрат, прямоугольник и треугольник. Они также изучают различные свойства этих фигур, такие как количество сторон, углов и длин сторон. Ученики также учатся решать геометрические задачи и строить фигуры на координатной плоскости.
В начальном курсе также изучаются темы измерения и анализа данных. Ученики учатся измерять длину, массу, время и объем. Они также изучают графики и диаграммы и учатся анализировать данные, представленные в них. Эти навыки помогают детям понять и интерпретировать информацию, представленную в графическом виде.
Начальный курс математики призван развить у детей основные математические навыки, которые они будут использовать во всей своей жизни. Он помогает им развить логическое мышление, аналитические и проблемно-ориентированные навыки. Изучение математики также помогает детям развить навыки решения задач, критического мышления и коммуникации. Начальный курс математики является важным этапом в образовании, который положит основу для дальнейшего изучения математики в старших классах и в дальнейшей жизни.
Числа и арифметика

Ученики учатся считать и записывать числа, узнают процедуры сложения, вычитания, умножения и деления. Они также изучают основные свойства чисел, такие как четность, нечетность, простота и составные числа.
Важным аспектом этого раздела является развитие навыков решения простых математических задач. Ученики учатся анализировать информацию, формулировать вопросы, находить решения и проверять свои ответы.
Числа и арифметика предоставляют ученикам базовые математические навыки, которые они могут применять в повседневной жизни и в дальнейшем образовании. Они также помогают развить логическое мышление, абстрактное мышление и решение проблем.
В конечном итоге, изучение чисел и арифметики является необходимым шагом в математическом образовании и помогает ученикам развиться в компетентных и уверенных в своих математических навыках людей.
Видео по теме:
Геометрия и формы

Одной из первых тем, которую изучают в геометрии, является понятие точки. Ученики узнают, что точка является основным элементом геометрии и не имеет ни размеров, ни формы.
Далее ученики изучают понятия линии и отрезка. Линия — это прямая, которая не имеет начала и конца. Отрезок — это часть линии, ограниченная двумя точками.
Круг и окружность — это также важные геометрические фигуры. Ученики узнают, что круг — это множество всех точек, находящихся на одинаковом расстоянии от центра. Окружность — это граница круга.
Для измерения геометрических фигур ученики учатся использовать различные инструменты. Один из них — линейка, которая помогает измерять отрезки.
Также в рамках изучения геометрии ученики изучают понятия угла, треугольника, прямоугольника, квадрата, параллелограмма, трапеции и других геометрических фигур.
ФигураОписание
| Треугольник | Фигура, состоящая из трех отрезков, соединяющихся между собой. |
| Прямоугольник | Фигура, у которой все углы прямые и противоположные стороны равны. |
| Квадрат | Фигура, у которой все стороны равны и все углы прямые. |
| Параллелограмм | Фигура, у которой противоположные стороны параллельны. |
| Трапеция | Фигура, у которой две стороны параллельны, а две другие — нет. |
Изучение геометрии и форм позволяет ученикам развивать навыки анализа и решения проблем, а также понимать пространственные отношения и взаимосвязи между геометрическими объектами.
Алгебра и уравнения

Уравнение — это математическое выражение, которое содержит одну или несколько переменных и знак равенства. Решение уравнения — это значение переменных, при которых уравнение становится верным.
В начальном курсе математики дети изучают основные понятия алгебры, такие как операции с числами (сложение, вычитание, умножение, деление), свойства операций, работа с переменными, алгебраические выражения и уравнения.
Они учатся решать простые уравнения и применять алгебраические методы для решения задач. Научившись анализировать и решать уравнения, дети развивают логическое мышление, абстрактное мышление и умение применять математические методы на практике.
Вопрос-ответ:
Зачем нужен начальный курс математики?
Начальный курс математики является основой для дальнейшего изучения математики. Он помогает развить логическое мышление, абстрактное мышление, аналитические навыки и решение проблем. Также он позволяет применять математические методы в реальных ситуациях и повышает общую культуру.
Какие основные темы входят в начальный курс математики?
Основные темы начального курса математики включают в себя: арифметику (сложение, вычитание, умножение, деление), геометрию (геометрические фигуры, периметр, площадь), алгебру (переменные, уравнения), вероятность и статистику (вероятность событий, среднее значение).
Что такое арифметика?
Арифметика — это наука о числах и операциях над ними, таких как сложение, вычитание, умножение и деление. В начальном курсе математики изучаются основные понятия арифметики, а именно сложение, вычитание, умножение и деление чисел, а также работа с десятичными дробями, процентами и пропорциями.
Что такое геометрия?
Геометрия — это наука о пространственных фигурах и их свойствах. В начальном курсе математики изучаются основные понятия геометрии, такие как геометрические фигуры (треугольники, квадраты, прямоугольники и т. д.), их периметр и площадь, а также работа с координатной плоскостью и построение графиков.
Функции и графики

График функции – это графическое представление зависимости между входными и выходными значениями функции. Он строится на плоскости, где по горизонтальной оси откладываются входные значения, а по вертикальной оси – выходные значения.
На начальном курсе математики в школе изучаются основные типы функций и их графики:
- Линейная функция. График линейной функции – это прямая линия. Уравнение линейной функции имеет вид y = kx + b, где k и b – коэффициенты.
- Квадратичная функция. График квадратичной функции – это парабола. Уравнение квадратичной функции имеет вид y = ax^2 + bx + c, где a, b и c – коэффициенты.
- Экспоненциальная функция. График экспоненциальной функции – это плавно возрастающая или убывающая кривая. Уравнение экспоненциальной функции имеет вид y = ab^x, где a – начальное значение, b – база экспоненты.
- Логарифмическая функция. График логарифмической функции – это плавно возрастающая или убывающая кривая. Уравнение логарифмической функции имеет вид y = logb(x), где b – база логарифма.
Изучение функций и графиков позволяет учащимся понять и описывать различные зависимости, решать уравнения и неравенства, а также применять математические модели в реальных задачах.
Вероятность и статистика
Вероятность позволяет оценить вероятность возникновения определенного события. Она основана на анализе возможных исходов и их вероятностей. Вероятностные методы используются во многих областях, таких как статистика, физика, экономика и медицина.
Статистика, в свою очередь, занимается сбором, анализом и интерпретацией данных. Она позволяет делать выводы о генеральной совокупности на основе выборочных данных. Статистические методы используются для прогнозирования, принятия решений и проверки гипотез.
Изучение вероятности и статистики помогает развить логическое мышление, аналитические навыки и способность принимать обоснованные решения на основе данных. Эти знания также имеют практическое применение в повседневной жизни, например, при оценке рисков, принятии финансовых решений или анализе результатов исследований.
Тригонометрия и геометрические преобразования

Геометрические преобразования – это операции, которые изменяют положение и форму геометрических фигур. В начальном курсе математики ученики изучают основные преобразования: поворот, симметрию и смещение. Они учатся выполнять эти преобразования в плоскости, используя различные инструменты и методы. Геометрические преобразования широко применяются в архитектуре, дизайне, компьютерной графике и других областях.
Математическое рассуждение и доказательства

Доказательство – это логически стройное объяснение или вывод, которое подтверждает истинность или ложность утверждений. Доказательства являются неотъемлемой частью математического исследования и представляют собой последовательность логических шагов, начиная с известных фактов и заканчивая требуемым результатом.
В процессе обучения математическому рассуждению и доказательству дети учатся работать с аксиомами, определениями, теоремами и леммами. Они учатся строить логические цепочки и находить нужные доказательства для решения задач. Это позволяет развивать абстрактное и логическое мышление, а также улучшает умение формулировать свои мысли и аргументировать свои решения.
Важно отметить, что математическое рассуждение и доказательства не только развивают умственные процессы, но и помогают ученикам лучше понимать математические понятия и законы. Они дают возможность глубже вникнуть в суть математических задач и проблем, а также находить новые подходы к решению проблем.


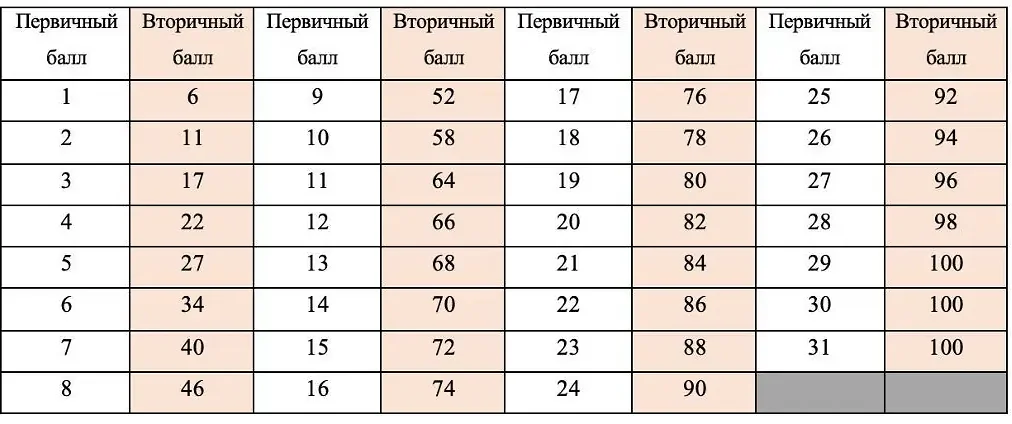

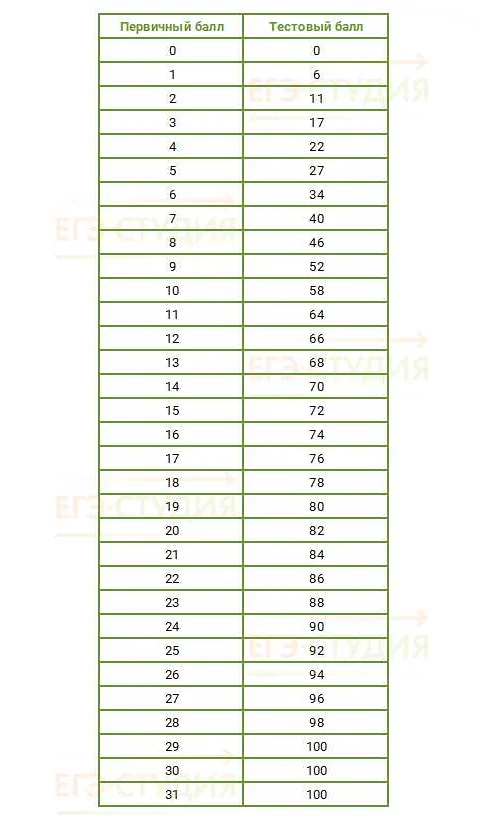
Статья очень полезная и интересная. В ней автор подробно описывает основные темы начального курса математики, которые включают в себя такие понятия, как числа, операции с числами, геометрия и алгебра. Мне понравилось, как автор дает примеры и объясняет каждую тему, делая материал понятным даже для тех, кто не имеет большого опыта в изучении математики. Я считаю, что такая статья будет полезной как для школьников, изучающих математику, так и для взрослых, кто хочет освежить свои знания. Благодаря этой статье я лучше поняла структуру начального курса математики и смогла вспомнить некоторые важные понятия. Спасибо автору за такую информативную статью!