Параметр в математике как решать

Узнайте, как правильно решать параметры в математике. Понятные объяснения и примеры. Получите навыки решения задач с параметром в математике.

Параметр – это величина, которая может принимать различные значения в зависимости от условий задачи. В математике параметры широко используются для описания и решения различных задач. Умение обращаться с параметрами является важным навыком для математика.

Решение задач с параметром требует специфического подхода и применения соответствующих методов. Необходимо учитывать все условия задачи и выражать все величины через параметр. Затем, используя алгебраические методы, можно решить полученное уравнение или систему уравнений и найти значения параметра и других величин.

Примером задачи с параметром может служить задача о нахождении значения параметра, при котором уравнение имеет решение. Для этого необходимо выразить все величины через параметр, решить уравнение и найти значения параметра, при которых уравнение выполняется.

Параметры также широко используются в геометрии. Например, в задачах на построение фигур или нахождение их свойств можно использовать параметры для описания различных случаев. Работа с параметрами помогает найти общие закономерности и упрощает решение задач.

Определение и основные понятия

Задача с параметром — это задача, в которой одна или несколько переменных являются параметрами. Решение такой задачи требует нахождения значений параметров, при которых выполняются определенные условия или соотношения.

Значение параметра — это конкретное число, подставляемое вместо параметра в уравнение или функцию. Значение параметра может варьироваться в зависимости от условий задачи.

Зависимость от параметра — это связь между переменными и параметрами. Зависимость показывает, как изменение значения параметра влияет на значения других переменных.

Ограничения параметра — это условия, которые накладываются на значение параметра в задаче. Ограничения могут быть заданы в виде неравенств, уравнений или других условий.

Исследование параметра — это процесс определения диапазона значений параметра, при которых выполняются определенные условия или соотношения. Исследование параметра позволяет найти особые значения, при которых происходят изменения в решении задачи.

Примеры решения задач с параметром — это конкретные задачи, которые решаются с использованием параметров. Примеры могут включать поиск максимального или минимального значения, решение систем уравнений или нахождение точек пересечения графиков.

Параметры в уравнениях и системах

Параметры в уравнениях и системах играют важную роль при решении математических задач. Они представляют собой числовые значения или символы, которые влияют на результат уравнений или систем уравнений.

Параметры могут быть известными или неизвестными величинами. Когда параметры известны, их значения уже определены, и их можно подставить в уравнение или систему уравнений для получения конкретного ответа. Например, в уравнении вида ax + b = 0, параметры a и b уже известны, и их значения можно найти, заменяя их числами или символами.

Однако, в некоторых случаях параметры могут быть неизвестными величинами, которые нужно найти. В таких случаях, параметры могут быть обозначены буквами, такими как x или y, и требуется найти значения этих параметров, удовлетворяющие уравнению или системе уравнений. Например, в системе уравнений вида:

• 2x + y = 5
• x — y = 1

параметры x и y являются неизвестными величинами, и нужно найти их значения, удовлетворяющие обоим уравнениям.

Решение уравнений или систем уравнений с параметрами может быть достигнуто с помощью различных методов, таких как подстановка, метод Гаусса и метод Гаусса-Жордана. В зависимости от сложности и типа уравнений, выбор метода может быть различным.

В простых случаях, где параметры являются числами, решение может быть найдено аналитически или с использованием калькулятора. Однако, в более сложных случаях, может потребоваться использование компьютерных программ или специализированных математических программ для решения уравнений с параметрами.

Имея понимание о параметрах и их роли в уравнениях и системах, можно более эффективно решать математические задачи и находить значения параметров, которые удовлетворяют условиям задачи.

Метод подстановки и его применение

Применение метода подстановки позволяет найти значения параметров, которые удовлетворяют заданным условиям. Для этого необходимо:

1. Выбрать одно из условий, содержащих параметр.
2. Подставить вместо параметра известное значение.
3. Вычислить значение выражения с подставленным параметром.
4. Проверить, удовлетворяет ли полученное значение заданному условию.
5. Если значение удовлетворяет условию, то это и будет искомым значением параметра.

Метод подстановки особенно полезен при решении уравнений и неравенств, содержащих параметры. Он позволяет найти все значения параметра, при которых уравнение или неравенство выполняются.

Применение метода подстановки требует аккуратности и внимания. Необходимо правильно выбрать значения для подстановки и корректно вычислить результат. В случае сложных выражений может потребоваться дополнительное алгебраическое преобразование перед подстановкой.

Таким образом, метод подстановки является эффективным инструментом для решения задач, в которых присутствуют параметры. Он позволяет найти значения параметров, удовлетворяющие заданным условиям, и является важным компонентом математического анализа и алгебры.

Нахождение значений параметров

Для того чтобы найти значения параметров в математических задачах, необходимо учесть условия задачи и использовать соответствующие методы решения.

Один из способов нахождения значений параметров – подстановка известных значений в уравнение или систему уравнений и решение полученных уравнений. Например, если дано уравнение вида ax + b = c, где a, b и c – параметры, а x – неизвестная, можно подставить известные значения параметров и решить уравнение для нахождения значения x.

Еще один способ нахождения значений параметров – использование условий задачи для составления системы уравнений. Например, если дана задача о распределении денег между несколькими людьми с известными соотношениями, можно составить систему уравнений, где параметрами будут являться доли каждого человека, а значениями параметров – неизвестные доли, которые нужно найти.

Также существуют специальные методы решения задач с параметрами, такие как метод подбора и метод замены. Метод подбора заключается в последовательной подстановке различных значений параметров и проверке соответствия условиям задачи. Метод замены предполагает замену параметров на другие переменные, что позволяет упростить систему уравнений и найти значения параметров.

Важно помнить, что в задачах с параметрами могут быть различные варианты решения, и в зависимости от условий задачи нужно выбирать наиболее подходящий метод.

Решение задач с параметром

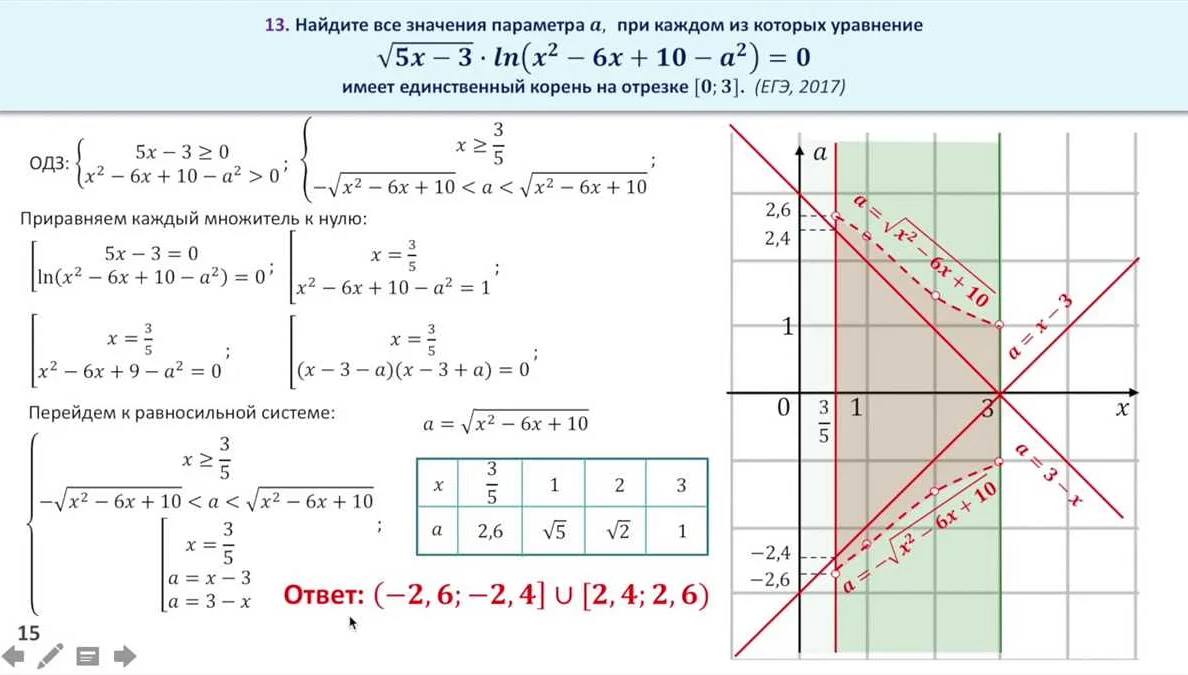
1. Определение параметра. Вначале необходимо определить, какую величину будет представлять параметр в задаче. Например, в задаче о двух числах, сумма которых равна 10, можно ввести параметр x, который будет представлять первое число.
2. Составление уравнений или неравенств. Далее необходимо составить уравнения или неравенства, используя параметр. В случае с задачей о двух числах, сумма которых равна 10, можно составить уравнение x + y = 10, где y – второе число.
3. Решение уравнений или неравенств. После составления уравнений или неравенств необходимо решить их относительно параметра. В случае с уравнением x + y = 10, можно решить его относительно x, получив x = 10 — y.
4. Подстановка найденных значений параметра. После нахождения значения параметра, необходимо подставить его в исходную задачу и проверить, что оно удовлетворяет условию. Например, если найденное значение параметра x = 5, то можно подставить его в исходное уравнение x + y = 10 и проверить, что получится верное равенство: 5 + y = 10.
5. Ответ. В конечном итоге, необходимо представить ответ на задачу, используя найденные значения параметра. Например, в задаче о двух числах, сумма которых равна 10, можно ответить, что первое число равно 5, а второе число равно 5.

Решение задач с параметром может быть полезным при решении различных типов задач, таких как задачи на нахождение площадей, объемов, времени и других величин. Оно позволяет упростить решение задачи и найти общую формулу или закономерность, которая позволяет находить значения в зависимости от параметра.

Графическое представление параметров

График – это двумерное представление данных, где параметр меняется по одной оси, а значение функции – по другой. На графике можно наглядно увидеть, как изменяется значение функции в зависимости от параметра, и определить его значения в различных точках.

Диаграмма – это графическое представление данных в виде столбцов, круговой диаграммы или других геометрических фигур. Диаграммы позволяют сравнивать значения параметров и наглядно иллюстрировать распределение данных.

Графическое представление параметров часто используется для анализа функций, определения их экстремумов, нахождения интервалов монотонности и других характеристик. Оно помогает увидеть закономерности и тренды, а также делает математические концепции более доступными и понятными.

Важно уметь интерпретировать графическое представление параметров и использовать его для решения задач. Анализ графиков и диаграмм позволяет делать выводы о характере изменения параметра и его влиянии на функцию или систему уравнений.

Графическое представление параметров – мощный инструмент, который помогает не только найти значения параметра, но и лучше понять и оценить их влияние на решение математических задач.

Типичные ошибки и их исправление

В процессе решения задач, связанных с параметрами, часто совершаются определенные ошибки. Рассмотрим некоторые из них и способы их исправления:

• Неправильное определение параметра: важно правильно понять, что именно является параметром в задаче. Часто ошибочно выбираются конкретные значения вместо переменной, а это может привести к неверным решениям. Перечитайте условие задачи и убедитесь, что вы правильно определили параметр.
• Ошибки в алгоритме решения: неправильно составленный алгоритм может привести к неверному результату. Проверьте свои вычисления и убедитесь, что вы правильно следуете каждому шагу решения. Если необходимо, перепроверьте свои выкладки или используйте другой метод решения.
• Неправильное использование формул и уравнений: в задачах с параметрами часто применяются различные формулы и уравнения. Ошибка может возникнуть из-за неправильного использования этих формул или неверного преобразования уравнений. Перепроверьте свои выкладки и убедитесь, что вы правильно применили нужные формулы и уравнения.
• Неправильный выбор значений параметра: в некоторых задачах требуется найти определенные значения параметра, которые удовлетворяют определенным условиям. Ошибка может возникнуть из-за неправильного выбора значений параметра или неправильной интерпретации условий задачи. Перечитайте условие задачи и убедитесь, что вы правильно выбрали значения параметра.
• Недостаточное количество уравнений: в задачах с параметрами часто требуется составить систему уравнений для нахождения значений параметра. Ошибка может возникнуть из-за недостаточного количества уравнений или неверного составления системы. Убедитесь, что вы правильно составили систему уравнений и что в ней есть достаточное количество уравнений для определения значений параметра.

Исправление этих ошибок требует внимательности и аккуратности при решении задач. Уделите достаточно времени на проверку каждого шага решения и перепроверку конечного результат, чтобы избежать неверных ответов.

Практические примеры и задания

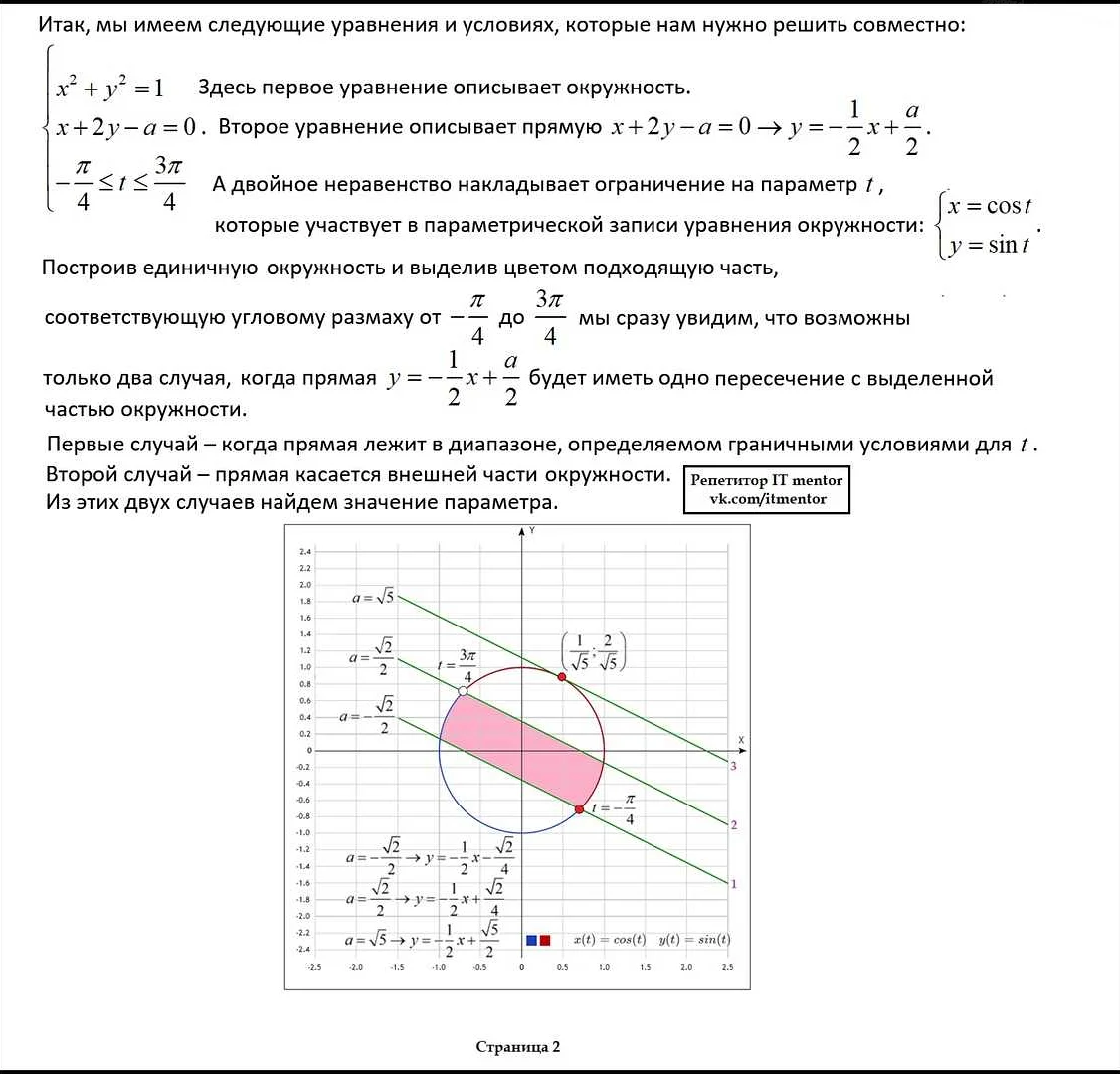
Для лучшего понимания параметров и их применения в математике, рассмотрим несколько практических примеров и заданий:

Пример 1:

Найдите значение функции f(x) = 2x + 3 при x = 5.

Решение:

Подставим значение x = 5 в функцию:

f(5) = 2 * 5 + 3 = 10 + 3 = 13

Ответ: f(5) = 13

Пример 2:

Решите уравнение 4x — 6 = 10.

Решение:

Перенесем 6 на другую сторону уравнения:

4x = 10 + 6 = 16

Разделим обе части уравнения на 4:

x = 16/4 = 4

Ответ: x = 4

Задание 1:

Найдите значение функции g(x) = x^2 — 5x + 6 при x = 2.

Задание 2:

Решите уравнение 3y + 2 = 8.

Задание 3:

Найдите корни квадратного уравнения 2x^2 — 5x — 3 = 0.

Попробуйте решить данные примеры и задания самостоятельно. Если у вас возникнут трудности, обратитесь к учебнику или преподавателю для получения дополнительной помощи.

Вопрос-ответ:

Какой смысл имеет понятие «параметр» в математике?

В математике параметр — это переменная, которая используется для нахождения значений функции или решения уравнения. Он позволяет задавать различные условия и варьировать значения, чтобы получить нужный результат.

Как решать задачи с параметром в математике?

Для решения задач с параметром необходимо сначала записать уравнение или систему уравнений, включающих данный параметр. Затем следует анализировать условия задачи и находить значения параметра, при которых выполняются эти условия. Нахождение этих значений позволяет найти решение задачи.

Как найти значения параметра в математике?

Для нахождения значений параметра в математике нужно решить уравнение или систему уравнений, в которых параметр выступает как неизвестная. Решение такого уравнения позволяет найти значения параметра, при которых уравнение выполняется.

Как использовать параметр для нахождения значений функции?

Для использования параметра в математике для нахождения значений функции нужно подставить значение параметра в выражение функции и вычислить его значение. При этом параметр может быть произвольным числом, которое позволяет задавать различные условия и варьировать результат.

Как найти значения параметра, при которых функция имеет особые точки?

Чтобы найти значения параметра, при которых функция имеет особые точки, необходимо решить уравнение, приравнивающее производную функции к нулю. Полученные значения параметра будут являться значениями, при которых функция имеет особые точки (максимумы, минимумы или точки перегиба).

Что такое параметр в математике?

Параметр в математике — это символ, который представляет собой неизвестное число или переменную в уравнении или выражении. Он позволяет установить, как изменение значения параметра влияет на значение уравнения или выражения.

Видео по теме: