Что такое площадь 4 класс математика

Площадь в математике для учащихся 4 класса – это понятие, которое помогает измерить площадь фигуры. Статья расскажет, как вычислить площадь различных геометрических фигур и предоставит примеры задач для тренировки.

Понятие площади является одним из основных понятий в математике. Она используется для измерения площади поверхностей и фигур. Площадь позволяет нам определить, насколько пространства занимает определенная фигура или объект. Площадь измеряется в квадратных единицах, таких как квадратные метры (м²) или квадратные сантиметры (см²).

В 4 классе ученики начинают изучать понятие площади и решать примеры, связанные с этой темой. Они узнают, как найти площадь прямоугольника, треугольника и квадрата. Для этого они используют формулы, которые позволяют вычислить площадь этих фигур.

Например, чтобы найти площадь прямоугольника, необходимо умножить длину на ширину. Формула для вычисления площади прямоугольника выглядит следующим образом: Площадь = Длина × Ширина.

Ученики также узнают, как сравнивать площади различных фигур и задачи на нахождение площади становятся все сложнее. Например, они могут получить задание найти площадь сложной фигуры, составленной из нескольких прямоугольников или треугольников. В таких задачах ученикам приходится разбивать фигуру на более простые части и вычислять площади каждой из них, а затем складывать полученные значения.

Изучение понятия площади в 4 классе является важным шагом в математическом образовании учеников. Оно помогает развить навыки анализа и логического мышления, а также применять полученные знания на практике при решении задач.

Понятие площади

Для измерения площади различных фигур существуют формулы. Например, площадь квадрата можно найти, умножив длину стороны на саму себя: S = a * a, где S — площадь, а a — длина стороны.

Также существуют специальные единицы измерения площади. Например, один квадратный метр — это площадь квадрата со стороной в 1 метр. Один квадратный сантиметр — это площадь квадрата со стороной в 1 сантиметр.

Понятие площади важно во многих областях, таких как архитектура, геометрия, строительство и даже география. Зная площадь различных фигур, мы можем рассчитывать их размеры и проводить различные вычисления.

Что такое площадь

Площадь является важным понятием в математике и находит широкое применение в различных областях, таких как геометрия, физика, архитектура и география.

Для измерения площади используются различные единицы, такие как квадратные метры (м²), квадратные километры (км²), квадратные сантиметры (см²) и другие.

Площадь можно вычислить для различных геометрических фигур, таких как квадраты, прямоугольники, треугольники и круги. Для каждой фигуры существуют специальные формулы, позволяющие вычислить ее площадь.

Например, площадь квадрата можно найти, умножив длину его стороны на саму себя. Для прямоугольника площадь равна произведению длины и ширины, а для треугольника — половине произведения длины основания на высоту.

Понимание площади помогает нам решать различные задачи, связанные с измерением площадей поверхностей и планированием пространства.

Как измеряется площадь

Площадь измеряется в квадратных единицах. Основными единицами измерения площади в СИ (системе международных единиц) являются квадратные метры (м2).

Для измерения площади прямоугольника необходимо умножить длину одной его стороны на длину другой стороны.

Например, если стороны прямоугольника равны 5 метров и 3 метра, то площадь этого прямоугольника будет равна 5 метров * 3 метра = 15 квадратных метров.

В других случаях, когда фигура не является прямоугольником, для измерения площади используются специальные формулы, которые зависят от вида фигуры.

Например, для измерения площади треугольника используется формула: площадь = (основание * высота) / 2.

Таким образом, зная длину основания и высоту треугольника, можно вычислить его площадь.

Измерение площади является важным и широко используется в жизни, например, при расчете площади участков, построек, полей, а также при решении задач в математике и других науках.

Понятие площади в математике

Понятие площади является важным в математике и находит применение в различных областях, таких как геометрия, физика, архитектура и другие.

Площадь фигуры можно вычислить разными способами в зависимости от ее формы. Например, для прямоугольника площадь можно найти, умножив длину на ширину. Для круга площадь можно найти, умножив квадрат радиуса на число π (пи).

Понимание площади помогает решать задачи, связанные с расчетом площадей земельных участков, площадей комнат, площадей полей и других объектов. Также оно позволяет проводить сравнения и анализировать различные фигуры, их размеры и формы.

Как рассчитывается площадь

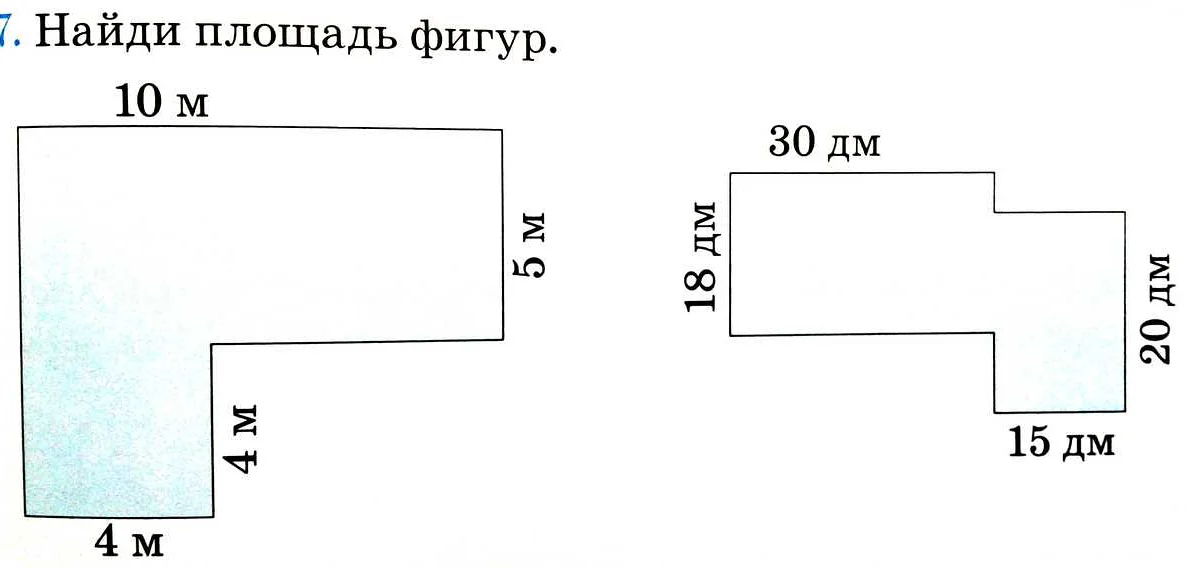
Для прямоугольника площадь рассчитывается по формуле: площадь = длина × ширина. Например, если у прямоугольника длина равна 5 см, а ширина – 3 см, то его площадь будет равна 5 × 3 = 15 см².

У квадрата все стороны равны между собой, поэтому его площадь можно вычислить по формуле: площадь = сторона × сторона. Например, если сторона квадрата равна 4 см, то его площадь будет равна 4 × 4 = 16 см².

Для треугольника площадь рассчитывается по формуле: площадь = (основание × высота) / 2. Например, если у треугольника основание равно 6 см, а высота – 4 см, то его площадь будет равна (6 × 4) / 2 = 12 см².

Для круга площадь можно вычислить по формуле: площадь = π × радиус², где π (пи) – математическая константа, примерное значение которой равно 3,14. Например, если радиус круга равен 7 см, то его площадь будет равна 3,14 × 7² ≈ 153,86 см².

Таким образом, рассчитывая площадь разных геометрических фигур по соответствующим формулам, можно получить точное значение площади и использовать его в решении задач по математике, геометрии и других областях.

Примеры задач на расчет площади

Пример 1:

Найдите площадь прямоугольника, если его длина равна 5 см, а ширина – 3 см.

Решение:

Площадь прямоугольника вычисляется по формуле: площадь = длина × ширина.

Подставляем значения в формулу: площадь = 5 см × 3 см = 15 см2.

Ответ: площадь прямоугольника равна 15 см2.

Пример 2:

Найдите площадь треугольника, если его основание равно 8 см, а высота – 4 см.

Решение:

Площадь треугольника вычисляется по формуле: площадь = (основание × высота) / 2.

Подставляем значения в формулу: площадь = (8 см × 4 см) / 2 = 16 см2.

Ответ: площадь треугольника равна 16 см2.

Пример 3:

Найдите площадь круга, если его радиус равен 6 см.

Решение:

Площадь круга вычисляется по формуле: площадь = π × радиус2, где π – математическая константа, приближенное значение которой равно 3,14.

Подставляем значения в формулу: площадь = 3,14 × 6 см × 6 см ≈ 113,04 см2.

Ответ: площадь круга примерно равна 113,04 см2.

Задачи на площадь в 4 классе

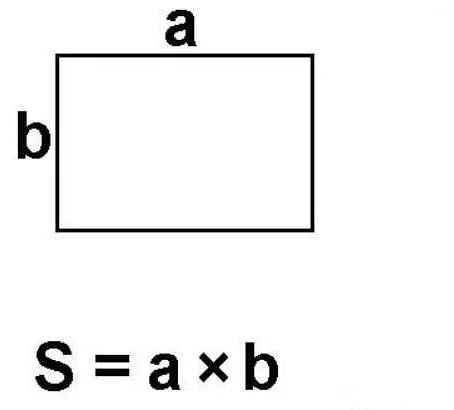
Пример задачи:

Задача 1: Вася решил выложить дорожку в своем саду. Он купил 12 квадратных плиток размером 2 на 2 метра каждая. Какая площадь будет занята этой дорожкой?

Решение: Площадь одной плитки равна 2 метра на 2 метра, то есть 4 квадратных метра. У Васи 12 таких плиток, поэтому площадь занятой дорожки будет равна 4 квадратных метра умножить на 12, то есть 48 квадратных метров.

Таким образом, площадь занятой дорожкой будет 48 квадратных метров.

Такие задачи помогают развивать логическое мышление, умение применять изученные математические понятия и операции на практике.

Видео по теме:

Вопрос-ответ:

Как определить площадь фигуры?

Площадь фигуры можно определить путем измерения площади ее поверхности. Для этого необходимо знать форму фигуры и использовать соответствующую формулу для расчета площади.

Какая формула используется для расчета площади прямоугольника?

Для расчета площади прямоугольника необходимо умножить длину одной его стороны на длину другой стороны: S = a * b, где S — площадь, а и b — длины сторон прямоугольника.

Какая формула используется для расчета площади квадрата?

Для расчета площади квадрата необходимо умножить длину одной его стороны на саму себя: S = a * a, где S — площадь, а — длина стороны квадрата.

Какая формула используется для расчета площади треугольника?

Для расчета площади треугольника необходимо умножить длину его основания на высоту, опущенную на это основание: S = (a * h) / 2, где S — площадь, а и h — соответственно длина основания и высота треугольника.

Какая формула используется для расчета площади круга?

Для расчета площади круга необходимо умножить квадрат радиуса на число Пи: S = r^2 * Пи, где S — площадь, а r — радиус круга.

Как можно определить площадь фигуры?

Площадь фигуры можно определить с помощью формулы или геометрических методов. В случае прямоугольника, площадь можно вычислить, умножив длину на ширину. Для круга площадь можно найти, умножив квадрат радиуса на число пи. Для других фигур может потребоваться использовать специальные формулы или разбить фигуру на более простые части и сложить их площади.

Какие примеры задач по площади можно решить в 4 классе?

В 4 классе можно решать простые задачи на вычисление площади прямоугольников, квадратов, треугольников и кругов. Например, можно попросить ученика найти площадь прямоугольника со сторонами 5 и 3, или площадь треугольника с основанием 6 и высотой 4. Также можно дать задачу на вычисление площади комнаты, используя измерения длины и ширины.

Задача на расчет площади прямоугольника

Рассмотрим следующую задачу: у нас есть прямоугольник со сторонами 5 см и 8 см. Необходимо найти его площадь.

Для решения данной задачи нужно умножить длину прямоугольника на его ширину:

Площадь = Длина × Ширина

В данном случае:

Площадь = 5 см × 8 см = 40 см²

Таким образом, площадь прямоугольника равна 40 квадратным сантиметрам.

Задача на расчет площади треугольника

Для решения задачи на расчет площади треугольника, нам необходимо знать формулу для расчета площади данной фигуры. Формула площади треугольника выглядит следующим образом:

Площадь треугольника (S) = (a * h) / 2

Где:

• a — длина основания треугольника
• h — высота треугольника, проведенная к основанию

Давайте рассмотрим пример задачи на расчет площади треугольника:

У нас есть треугольник с основанием длиной 6 см и высотой 4 см. Найдем его площадь.

Основание (a)Высота (h)Площадь (S)

6 см

4 см

(6 * 4) / 2 = 12 см2

Ответ: площадь треугольника равна 12 см2.

Таким образом, мы рассмотрели задачу на расчет площади треугольника и нашли ее решение.