Что такое площадь по математике 3 класс

Площадь по математике в 3 классе — это понятие, которое помогает определить площадь поверхности фигуры. В статье рассматриваются основные понятия и методы вычисления площади, которые помогут детям легче освоить эту тему. Также представлены примеры и задачи для самостоятельной работы.

Площадь — это важное понятие в математике, которое вводится уже в 3 классе. Площадь помогает нам измерять поверхность плоских фигур, таких как квадраты, прямоугольники и треугольники. Знание площади позволяет нам решать различные задачи, связанные с геометрией и измерениями.

Основная формула для вычисления площади простых фигур выглядит следующим образом: «площадь равна длине умноженной на ширину». Например, площадь прямоугольника можно найти, умножив длину прямоугольника на его ширину. Формулы для площади других фигур, таких как квадрат и треугольник, могут немного отличаться, но основная идея остается прежней — нужно умножить некоторые измерения фигуры, чтобы найти ее площадь.

Понимание площади имеет практическое значение в жизни. Например, зная площадь комнаты, можно рассчитать, требуется ли больше или меньше мебели для ее меблировки. Знание площади также помогает в строительстве и архитектуре, где необходимо рассчитать площадь земельного участка или площадь крыши.

Определение понятия «площадь» в математике

Площадь измеряется в квадратных единицах, например, квадратных сантиметрах (см2), квадратных метрах (м2) или квадратных дециметрах (дм2).

Чтобы найти площадь фигуры, необходимо знать ее форму и размеры. Для различных фигур существуют разные формулы для вычисления площади.

Например, площадь прямоугольника вычисляется по формуле:

Площадь = длина × ширина

Другие фигуры, такие как круг, треугольник или квадрат, имеют свои собственные формулы для вычисления площади.

Понимание понятия «площадь» помогает нам измерять и сравнивать размеры различных фигур и использовать их в различных задачах, связанных с пространством и геометрией.

Как вычислять площадь в 3 классе

Вычисление площади осуществляется путем умножения соответствующих сторон фигуры. Для прямоугольника, площадь которого несложно вычислить, нужно умножить длину на ширину. Например, если длина прямоугольника равна 5 см, а ширина – 3 см, то площадь будет равна 5 см × 3 см = 15 см².

Для квадрата площадь вычисляется аналогичным образом – нужно умножить длину стороны на саму себя. Если сторона квадрата равна 4 см, то площадь будет равна 4 см × 4 см = 16 см².

Если фигура состоит из нескольких прямоугольников, необходимо вычислить площадь каждого прямоугольника и сложить их. Например, если у нас есть фигура, состоящая из двух прямоугольников со сторонами 3 см и 4 см, то площадь будет равна 2 × (3 см × 4 см) = 2 × 12 см² = 24 см².

Таким образом, вычисление площади – это несложная задача, которую дети могут успешно решать уже в 3 классе. Это важное математическое понятие, которое помогает развивать логическое мышление и умение работать с числами.

ФигураФормула для вычисления площади

Прямоугольник	Площадь = длина × ширина
Квадрат	Площадь = сторона × сторона

Примеры задач на вычисление площади

1. Найдите площадь прямоугольника со сторонами 5 см и 3 см.

Для решения данной задачи нужно умножить длину одной стороны на длину другой стороны: 5 см * 3 см = 15 см².

Ответ: площадь прямоугольника равна 15 см².

2. Найдите площадь квадрата со стороной 7 м.

Площадь квадрата можно найти, умножив длину одной стороны на саму себя: 7 м * 7 м = 49 м².

Ответ: площадь квадрата равна 49 м².

3. Найдите площадь треугольника со сторонами 6 см, 8 см и 10 см.

Для нахождения площади треугольника с помощью формулы Герона, нужно вычислить полупериметр треугольника, который равен сумме всех сторон, деленной на 2: (6 см + 8 см + 10 см) / 2 = 12 см.

Затем, используя формулу Герона: S = √(p * (p — a) * (p — b) * (p — c)), где S — площадь треугольника, p — полупериметр, а, b, c — стороны треугольника, получаем:

S = √(12 см * (12 см — 6 см) * (12 см — 8 см) * (12 см — 10 см)) = √(12 см * 6 см * 4 см * 2 см) = √(576 см²) = 24 см².

Ответ: площадь треугольника равна 24 см².

ФигураСтороныПлощадь

Прямоугольник	5 см, 3 см	15 см²
Квадрат	7 м	49 м²
Треугольник	6 см, 8 см, 10 см	24 см²

Понятие «единица измерения площади»

В международной системе единиц (СИ) основной единицей измерения площади является квадратный метр (м²). Однако, в школьной программе для изучения площади используются простые и понятные единицы измерения, такие как квадратный сантиметр (см²) и квадратный дециметр (дм²).

1 квадратный сантиметр (см²) — это площадь квадрата со стороной 1 сантиметр.

1 квадратный дециметр (дм²) — это площадь квадрата со стороной 1 дециметр (10 сантиметров).

Для более крупных площадей могут использоваться другие единицы измерения, такие как квадратный метр (м²), гектар (га) или квадратный километр (км²).

Сравнение площадей разных фигур

Для сравнения площадей разных фигур мы можем использовать различные методы. Один из таких методов — сравнение по количеству квадратных единиц. Если мы имеем две фигуры и знаем, что одна из них имеет большую площадь, мы можем сравнить количество квадратных единиц в каждой фигуре. Фигура с большим количеством квадратных единиц будет иметь большую площадь.

Например, если у нас есть два прямоугольника, один со сторонами 4 см и 6 см, а другой со сторонами 5 см и 7 см, мы можем сравнить их площади, умножив длину на ширину каждого прямоугольника. В данном случае, площадь первого прямоугольника будет равна 24 квадратным сантиметрам, а площадь второго прямоугольника будет равна 35 квадратным сантиметрам. Таким образом, мы можем сказать, что второй прямоугольник имеет большую площадь.

Важно помнить, что для сравнения площадей фигур они должны быть одного вида, то есть иметь одну и ту же форму. Например, мы не можем сравнивать площадь прямоугольника и площадь треугольника, так как они имеют разную форму.

Сравнение площадей разных фигур позволяет нам определить, какая фигура имеет большую или меньшую площадь, что является важным навыком при решении задач из области геометрии.

Свойства площади

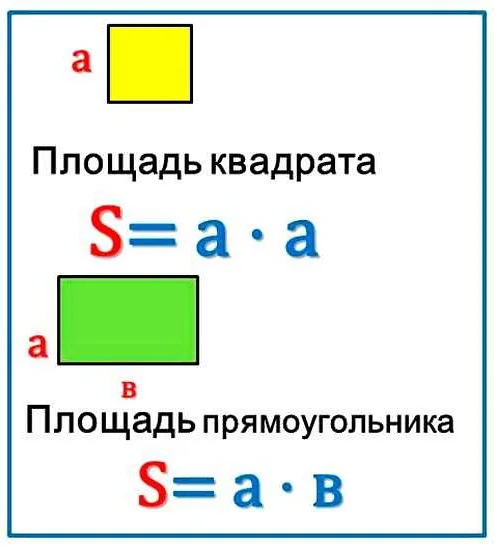
1. Коммутативность: Площадь фигуры не изменяется при изменении порядка ее составляющих частей. Например, площадь прямоугольника АВСD равна площади прямоугольника CDAB.

2. Аддитивность: Площадь объединения двух непересекающихся фигур равна сумме их площадей. Например, площадь фигуры ABCDEF равна сумме площадей фигур ABCD и EF.

3. Кратность: Если фигура состоит из нескольких одинаковых фигур, то площадь всей фигуры равна площади одной фигуры, умноженной на их количество. Например, площадь треугольника АВС равна площади треугольника ЕFG, а площадь фигуры АВСЕFG равна площади треугольника АВС, умноженной на 2.

4. Изменение масштаба: Площадь фигуры изменяется пропорционально квадрату масштабного коэффициента. Например, если все стороны прямоугольника увеличить в 2 раза, то его площадь увеличится в 4 раза.

5. Площадь точки: Площадь точки равна нулю, так как точка не имеет размеров.

6. Площадь линии: Площадь линии также равна нулю, так как линия является одномерным объектом.

7. Площадь поверхности: Площадь поверхности трехмерного тела равна сумме площадей всех его граней.

Знание свойств площади помогает в решении задач, связанных с вычислением площади фигур и их преобразованием.

Зачем знать понятие «площадь» в 3 классе

Понимание площади позволяет развить у детей навыки измерения, сравнения и классификации объектов по их размеру. Зная площадь, ребенок сможет сравнивать и оценивать, какая поверхность больше или меньше.

Понятие площади также важно для развития логического мышления и абстрактного мышления у детей. Они научатся анализировать и сравнивать геометрические фигуры на основе их площади.

Знание площади также помогает детям развивать навыки решения проблем и построения логических цепочек рассуждений. Они научатся применять эти навыки в повседневной жизни, включая решение задач и построение планов действий.

Кроме того, понятие площади является основой для изучения других математических концепций, таких как периметр, объем и т.д. Поэтому знание площади в 3 классе является важным фундаментом для дальнейшего изучения математики.

Вопрос-ответ:

Что такое площадь?

Площадь — это величина, которая показывает, сколько плоского пространства занимает фигура. Например, если у нас есть квадрат со стороной 4 см, то его площадь будет равна 16 квадратным сантиметрам.

Как вычислить площадь квадрата?

Для вычисления площади квадрата нужно умножить длину одной из его сторон на саму себя. Например, если сторона квадрата равна 5 см, то его площадь будет равна 25 квадратным сантиметрам.

Что такое геометрическая фигура?

Геометрическая фигура — это фигура, которая имеет определенную форму и размеры. Например, квадрат, круг, прямоугольник — все это геометрические фигуры.

Как вычислить площадь прямоугольника?

Для вычисления площади прямоугольника нужно умножить длину его стороны на ширину. Например, если длина прямоугольника равна 6 см, а ширина — 4 см, то его площадь будет равна 24 квадратным сантиметрам.

Можно ли вычислить площадь фигуры, если у нее нет прямых сторон?

Да, можно. Для этого нужно разбить фигуру на более простые части, например, на прямоугольники или треугольники, вычислить площадь каждой части и сложить их вместе. Например, для вычисления площади круга можно разбить его на много маленьких треугольников и просуммировать их площади.

Как объяснить понятие площади детям в 3 классе?

Площадь – это понятие в математике, которое обозначает, сколько места занимает фигура на плоскости. Как правило, площадь измеряется в квадратных единицах, таких как квадратные сантиметры или квадратные метры. Детям можно объяснить, что площадь – это площадь поверхности фигуры, то есть сколько квадратиков можно на нее поставить. Например, если у нас есть квадрат со стороной 5 сантиметров, то его площадь будет равна 25 квадратным сантиметрам, потому что на него можно поставить 25 квадратиков со стороной 1 сантиметр.

Какие есть примеры площади в повседневной жизни, которые можно показать детям в 3 классе?

Есть много примеров площади в повседневной жизни, которые можно показать детям в 3 классе. Например, можно показать им площадь стола, на котором можно поставить игрушки или книги. Также можно показать площадь комнаты, в которой они находятся, и объяснить, сколько квадратных метров занимает комната. Другой пример – площадь листа бумаги, на котором они могут рисовать. Важно, чтобы дети понимали, что площадь – это не только численное значение, но и конкретное место на плоскости.

Видео по теме: