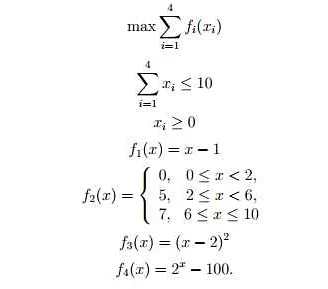Почему математика опирается на дискретность: причины и примеры

Статья рассказывает о том, почему математика дискретна и как ее применяют в современных технологиях. Открытия в области математической логики, теории графов и алгоритмов сделали возможным создание компьютерных систем и программного обеспечения.

Математика — это наука о количественных отношениях и пространстве. Применение математики в научных и практических областях очень широко, но не все знают, что она может быть дискретной или непрерывной. В этой статье мы рассмотрим основные причины того, почему математика может быть дискретной.

Дискретность математики связана с ее объектом изучения. Как правило, дискретные модели используются для решения проблем, которые могут быть представлены в виде дискретных или цифровых данных. Они не могут быть представлены в виде непрерывных функций, а только в виде конечного или бесконечного счетного числа значений.

Одной из причин, по которой математика является дискретной, является то, что многие системы, которые мы изучаем, являются дискретными. Например, информационные системы, цифровые сигналы или дискретные события в системах безопасности. Использование дискретной математики в этих системах позволяет благодаря точности и эффективности их построения и решения задач.

Определение дискретной математики

Дискретная математика – это раздел математики, который изучает дискретные объекты, такие как целые числа, конечные последовательности чисел, графы, деревья и т.д. Она является одной из основных областей математики, используемых в информатике, теории алгоритмов, криптографии и многих других областях науки и технологий.

Дискретная математика занимается расчетами на основе отдельных значений, а не на основе непрерывных значений, как это делает математика континуума. Это означает, что дискретная математика используется для решения проблем, в которых объекты или процессы имеют конечное количество значений или состояний. Также дискретная математика изучает свойства комбинаторики, графов и теории вероятности.

Ключевыми понятиями в дискретной математике являются множества, отношения, функции, алгоритмы и теория графов. Они используются для создания моделей и решения проблем в таких областях, как теория кодирования, теория игр, криптография, теория вычислительной сложности и многих других. Дискретная математика имеет широкое применение и является неотъемлемой частью современного научного и технологического прогресса.

Различия между дискретной и непрерывной математикой

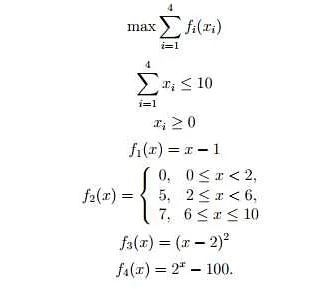
Математика может быть подразделена на две основные категории: дискретную и непрерывную. На первый взгляд они могут показаться похожими, но на самом деле очень отличаются друг от друга.

Дискретная математика описывает объекты, которые могут быть пронумерованы, отдельными элементами, имеющими конечное число значений. Например, количество студентов в классе, число деревьев в парке, количество страниц в книге. Дискретная математика рассматривает эти объекты как отдельные и не зависит непосредственно от времени.

С другой стороны, непрерывная математика включает в себя объекты, которые не могут быть пронумерованы, и которые имеют бесконечное число значений. Эту математику используют в физике, химии, экономике для описания непрерывных процессов, например, движения тела, колебаниям, функциям.

Существует также категория математики — комбинаторика, которая занимается перечислением комбинаций, упорядочиваний и размещений. Она использует дискретную математику и может быть применена в различных областях, например, в теории кодирования и криптографии.

Суммируя вышеизложенное, можно сказать, что главными различиями между дискретной и непрерывной математикой являются: дискретная математика рассматривает конечные объекты, имеющие определенное число значений и не зависящие от времени, тогда как непрерывная математика описывает бесконечно-значные объекты и зависит от времени.

Применение дискретной математики в компьютерных науках

Дискретная математика является неотъемлемой частью компьютерных наук и используется в большинстве прикладных областей, связанных с компьютерами. Она описывает структуру данных и алгоритмы, которые используются для решения задач в компьютерном программировании и криптографии.

Например, теория графов — это один из основных элементов дискретной математики, который широко используется в компьютерной науке для анализа и проектирования сетей, поисковых алгоритмов и теории сложности вычислений. Она помогает создавать эффективные алгоритмы, уменьшать время работы программ и ускорять вычисления.

Еще одной областью, где применяется дискретная математика, является теория формальных языков. Она используется для разработки компиляторов и интерпретаторов, создания формальных спецификаций языков программирования и разработки систем автоматической проверки доказательств.

Среди других областей, где применяется дискретная математика, можно назвать теорию автоматов, криптографию, теорию кодирования, теорию игр и многие другие.

Таким образом, дискретная математика играет важную роль в компьютерных науках и приложениях, связанных с компьютерами. Без нее невозможно представить работу с современными технологиями и системами, которые лежат в основе информационного общества.

Роль дискретной математики в технологиях шифрования

Шифрование – процесс преобразования открытого текста в закрытый, который становится недоступным для человека без специальных знаний и ключа. К основным задачам шифрования относится обеспечение конфиденциальности, целостности и аутентичности передаваемых данных. Решение этих задач возможно благодаря дискретной математике.

Алгоритмы шифрования используются во многих сферах – от защиты электронного письма до банковских транзакций и государственной тайны. Эффективное шифрование невозможно без применения принципов дискретной математики, таких как теория чисел, комбинаторика и теория графов.

Одним из наиболее распространенных методов шифрования является асимметричное шифрование. При использовании этого метода каждый пользователь имеет пару ключей – открытый и закрытый. Открытый ключ может использовать любой, кто хочет послать сообщение, а закрытый – только адресат сообщения. При этом данные, зашифрованные открытым ключом, могут быть расшифрованы только закрытым ключом.

Алгоритм RSA – один из наиболее широко используемых алгоритмов асимметричного шифрования, базируется на простых числах и теории чисел. Этот алгоритм обеспечивает надежную защиту информации и используется в таких областях, как электронная почта, интернет-банкинг, облачные сервисы и многие другие.

Таким образом, дискретная математика играет важную роль в разработке и применении современных технологий шифрования. Решения, основанные на принципах дискретной математики, обеспечивают защиту информации от несанкционированного доступа и являются необходимыми в нашей всё более цифровой экономике.

Преимущества использования дискретных моделей в науке и инженерии

Дискретные модели могут быть использованы в науке и инженерии для обработки и анализа информации. Они позволяют разбить данные на конечное количество элементов или дискретных значений. Использование дискретных моделей имеет ряд преимуществ:

• Универсальность: Дискретные модели широко применяются в различных сферах, таких как теория систем, теория информации, теория вероятности и математическая логика.
• Четкость и точность: Дискретные модели позволяют точно описывать и анализировать системы и процессы, а также проводить точные вычисления.
• Эффективность: Дискретные модели позволяют эффективно решать задачи, связанные с обработкой и анализом большого количества данных.
• Простота: Дискретные модели могут быть просты в использовании и понимании, что делает их доступными для широкой аудитории.

В целом, использование дискретных моделей в науке и инженерии может привести к более точным, эффективным и простым решениям различных задач.

Изучение графов и теории игр в дискретной математике

Дискретная математика является фундаментальной дисциплиной в информатике и является основой для многих приложений в области информационных технологий. В частности, изучение теории графов и теории игр является важной частью дискретной математики.

Графы являются абстрактными математическими объектами, которые используются для представления различных структур, таких как сети связей, деревья и другие. Теория графов обладает широким спектром приложений, от оптимизации маршрутов в городе до проектирования компьютерных сетей.

В теории игр изучается математическое моделирование стратегий и тактик, используемых в играх. Эта область математики играет важную роль в экономике, политике и общественных науках. Теория игр может помочь в принятии решений в различных областях, в том числе в бизнесе и в жизненных ситуациях.

Все это делает изучение графов и теории игр важной частью обучения дискретной математике. Студенты изучают основные понятия и методы, используемые в этих областях, и применяют их на практике в задачах оптимизации и принятия решений.

Таким образом, изучение графов и теории игр является неотъемлемой частью дискретной математики и имеет широкий спектр приложений в различных областях.

Применение дискретной математики в экономике и финансах

Дискретная математика является неотъемлемой частью современной экономики и финансов. Она используется для моделирования и решения различных бизнес-задач, а также для принятия важных экономических и финансовых решений.

Одним из примеров является поиск оптимального пути инвестирования. Дискретные математические методы позволяют рассчитать вероятность доходности в зависимости от выбранных инвестиционных стратегий. Они также могут помочь в прогнозировании изменений рыночной конъюнктуры и принятии соответствующих решений.

Другой важной областью является прогнозирование спроса на товары и услуги. Дискретные математические методы могут помочь в расчете оптимального уровня запасов продукции, а также в определении цен на товары.

Также дискретная математика используется для оптимизации работы логистических систем. Например, определение маршрутов доставки грузов, расчет необходимого количества транспортных средств и определение оптимального расписания перевозок.

В целом, дискретная математика позволяет более точно и эффективно решать различные проблемы в экономике и финансах, а также повышать эффективность бизнес-процессов. Она стала необходимой технологией для любой компании, которая хочет держать руку на пульсе экономических и финансовых процессов.

Разработка алгоритмов в дискретной математике

Дискретная математика широко применяется в различных областях науки и техники, в том числе, для разработки алгоритмов. Алгоритм – это последовательность шагов, необходимых для решения определенной задачи. Разработка алгоритмов – это процесс создания и оптимизации последовательности шагов для достижения желаемого результата.

Дискретная математика предоставляет набор инструментов для разработки алгоритмов, таких как теория графов, теория алгоритмов, комбинаторика и другие. Например, теория графов позволяет представить объекты и связи между ними в виде графа, что может быть полезно для разработки алгоритмов поиска кратчайшего пути в графе или решения задачи о раскраске графа.

Теория алгоритмов, в свою очередь, позволяет формализовать процесс решения задачи, определить сложность алгоритма и сравнить различные алгоритмы по эффективности и скорости работы. Комбинаторика может быть полезна для определения всех возможных комбинаций элементов и правил их сочетания, что может быть применено в алгоритмах оптимизации.

Таким образом, разработка алгоритмов в дискретной математике – это продуктивное слияние математических методов и практической задачи. Использование конкретных методов дискретной математики может способствовать ускорению и оптимизации последовательности шагов и повышению эффективности алгоритма в целом.

Обучение дискретной математике в образовательных учреждениях

Дискретная математика является одним из ключевых предметов в области информатики и кибернетики. Хорошее знание базовых понятий и методов дискретной математики существенно помогает в решении задач в области программирования, системной архитектуры, баз данных и других смежных областей.

Большинство вузов, где читаются специальности по IT, имеют дисциплины, связанные с дискретной математикой. Этот предмет изучается как в технических, так и в гуманитарных университетах. На протяжении всего курса ему уделяется большое внимание, начиная с представления базовых понятий о логике и алгебре до более глубоких тем, связанных с теорией графов и комбинаторикой.

Обучение дискретной математике дает необходимые знания для успеха в различных областях, не только в информационных и технологических. Оно также придает основы для изучения других математических дисциплин, например, дифференциальных уравнений и анализа.

В рамках курса дискретной математики студенты обучаются использованию конкретных инструментов, таких как программы для обработки данных и математических символьных вычислений. Они также проходят курсы лекций, которые позволяют им получить полное понимание ключевых понятий, на которых базируется дискретная математика.

Обучение дискретной математике в образовательных учреждениях является важным шагом для студентов, которые хотят заниматься IT и инженерной деятельностью. Большинство работодателей в этой области требуют хороших знаний в дискретной математике, и, следовательно, курсы по дискретной математике в университетах являются необходимыми для создания квалифицированной рабочей силы.

Связь дискретной математики с другими науками

Дискретная математика, в отличие от непрерывной, ставит в центр своего внимания объекты с конечным или счётным числом элементов. Она находит свое применение в множестве наук и областей, таких как:

1. 1. Криптография — наука об охране конфиденциальности и целостности информации. Криптография тесно связана с дискретной математикой благодаря применению теории чисел, комбинаторики, теории графов и других дисциплин;
   2. Компьютерные науки — дискретная математика играет важную роль в информатике и компьютерных науках, например, в алгоритмах, структурах данных, теории сложности вычислений и т.д.;
   3. Теория кодирования — наука о создании и использовании кодов для представления информации. Дискретная математика является фундаментальной для расширения теории кодирования и ее применения в различных отраслях:
      • Телекоммуникации;
      • Дизайн баз данных;
      • Генетика;
   4. Искусственный интеллект — разработка алгоритмов и методов для создания автоматического интеллектуального поведения. Изучение различных дискретных структур позволяет использовать эффективные алгоритмы для задания проблем и реализации значительно быстрее и точнее.

Дискретная математика имеет множество других связей и применений в науке и технологии, и она безусловно является неотъемлемой частью современного мира.

Выводы о важности изучения дискретной математики

1. Рост востребованности на рынке труда

Компьютеры и современные технологии имеют универсальное применение, что приводит к растущей востребованности математических специалистов. Знания в области дискретной математики позволяют эффективно работать с алгоритмами и программированием.

2. Углубление понимания процессов

Дискретная математика помогает углубить понимание процессов в различных научных областях — физике, биологии, социологии и других науках. Так, алгоритмы графовой теории применяются при анализе сложных систем и маршрутов движения в сетях.

3. Развитие мышления и умений

Изучение дискретной математики развивает мышление, логику и способствует приобретению навыков формального анализа. Основные понятия дискретной математики используются в криптографии, испытательных методах и принятии решений в бизнесе.

4. Новые возможности для исследований

Для научных исследований в области информатики и математики часто требуются знания дискретной математики. Она дает возможность рассматривать объекты в дискретных категориях и последовательностях, а также строить более точные модели и прогнозы.

5. Ключ к успеху в современном мире

Современный мир зависит от сетей и информационных технологий, а значит, от дискретной математики. Изучение и практическое применение дискретной математики позволяет успешно справляться с вызовами современного мира.

Вопрос-ответ:

Почему математика дискретная?

Математика дискретная, так как она занимается изучением объектов, которые принимают конечное или счётное множество значений. Это, в свою очередь, обусловлено тем, что многие объекты в реальном мире также проявляют дискретность, приводящую к необходимости использования такой математики.

Какие примеры дискретных объектов есть в реальном мире?

Примерами дискретных объектов могут служить цифры, натуральные числа, числа-идентификаторы, цифровые изображения, маршруты в путевых листах, персонажи в компьютерных играх и гамма-кванты в фотоне.

Каковы основные преимущества дискретной математики?

Основными преимуществами дискретной математики являются её возможность решения широкого круга задач, таких как комбинаторика, теория графов, вычислительные методы и другие. Также дискретная математика обладает простой структурой и логической связностью, что делает её удобной в применении и анализе.

Каким образом дискретная математика используется в компьютерных науках?

Дискретная математика находит широкое применение в компьютерных науках. Например, она используется в технике кодирования, криптографии, теории алгоритмов, планировании ресурсов и других областях.

В чём отличие дискретной математики от непрерывной?

Дискретная математика изучает объекты, которые принимают конечное или счётное множество значений, в то время как непрерывная математика занимается объектами, которые принимают бесконечное множество значений. Кроме того, вычисления в дискретной математике выполняются с целыми числами, а в непрерывной — с дробными.

Каковы основные инструменты дискретной математики?

Основными инструментами дискретной математики являются теория множеств, комбинаторика, теория графов, математическая логика и алгоритмы. Эти инструменты используются для формулировки и решения широкого спектра задач в различных областях исследования.

Каким образом дискретная математика используется в бизнесе и экономике?

Дискретная математика применяется в бизнесе и экономике для моделирования и анализа различных процессов и явлений. Например, она используется для определения оптимальных маршрутов доставки товаров, расписания производственных процессов, прогнозирования потребности в ресурсах и других областей.

Видео по теме: