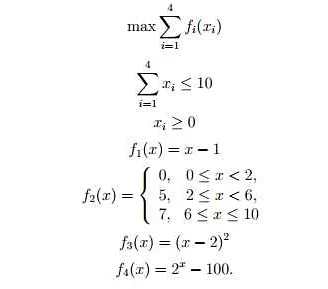Дискретная математика: чем она отличается от классической

Статья рассказывает о том, как дискретная математика отличается от классической. Здесь вы найдете примеры задач, решаемых методами дискретной математики, и объяснения основных понятий этой науки. Узнайте, почему дискретная математика так важна в компьютерных науках и других областях нашей жизни.

Дискретная математика – это раздел математики, который занимается изучением дискретных объектов, таких как целые числа, графы, алгоритмы и т.д. В отличие от классической математики, которая занимается изучением непрерывных объектов, дискретная математика имеет свои особенности и характеристики.

Одной из основных особенностей дискретной математики является использование дискретных элементов в качестве базовых объектов. Например, при изучении графов, вершины и ребра графа являются элементами, которые могут быть использованы для описания различных объектов. Дискретная математика также имеет свои специфические методы и инструменты для работы с дискретными объектами и структурами.

Дискретная математика имеет широкое применение в различных областях, таких как информатика, криптография, теория кодирования, теория графов, алгоритмы и т.д. Благодаря специфическим методам и инструментам дискретной математики, можно решать множество задач и проблем в этих областях и создавать новые изобретения и приложения.

Отличия дискретной математики от классической

Дискретная математика — это раздел математики, который изучает дискретные объекты, такие как целые числа, булевы значения, символы, строки и т.д. В отличие от этого, классическая математика изучает непрерывные объекты, такие как функции, дифференциальные уравнения, геометрические фигуры и т.д.

Дискретная математика используется в широком спектре областей, таких как информатика, криптография, теория графов, теория кодирования и многих других. В классической математике основное применение находит в геометрии, анализе, алгебре и других областях.

В дискретной математике используется логика, теория множеств, комбинаторика, графы, алгоритмы и многие другие математические инструменты для исследования дискретных объектов и их свойств. В классической математике, например, используются теория чисел, дифференциальные уравнения, тригонометрия и другие математические инструменты для изучения непрерывных объектов.

Важной отличительной чертой дискретной математики является то, что она позволяет точно определить и ограничить рассматриваемые объекты и их свойства. Это обуславливает ее широкое применение в различных областях, особенно в информатике. В то же время, классическая математика является более абстрактной и теоретической, что обуславливает ее применение в более узком круге задач.

Видео по теме:

Основные понятия

Дискретность — основной принцип дискретной математики, основанный на том, что все объекты, с которыми работает дискретная математика, дискретны, т.е. не могут принимать промежуточных значений. В отличие от классической математики, которая работает с непрерывными величинами, дискретная математика работает со счетными объектами, такими как целые числа, последовательности, графы и т.д.

Алгоритм — последовательность дискретных шагов, которые позволяют выполнить определенное действие или решить задачу. Алгоритмы используются во многих областях, таких как компьютерная наука, криптография, теория игр и других.

Логическая алгебра — раздел дискретной математики, который изучает основные логические операции и позволяет строить логические функции. Логическая алгебра используется в различных областях, включая электронику, компьютерную науку и другие.

Комбинаторика — область дискретной математики, которая изучает комбинаторные объекты, такие как перестановки, сочетания, размещения и другие. Комбинаторика находит свое применение в различных областях, включая теорию вероятностей, криптографию и другие.

Теория графов — раздел дискретной математики, который изучает свойства графов, т.е. системы вершин и ребер. Теория графов находит широкое применение в различных областях, включая теорию игр, социологию, транспортную логистику и другие.

Кодирование информации — процесс преобразования информации в форму, пригодную для передачи или хранения. Дискретная математика играет важную роль в этом процессе, определяя эффективные способы кодирования и декодирования информации.

Пример использования тега tableПонятиеОбласть применения

Дискретность	Теория алгоритмов, теория множеств, криптография и другие области
Алгоритм	Компьютерная наука, теория игр, криптография и другие области
Логическая алгебра	Электроника, компьютерная наука и другие области
Комбинаторика	Теория вероятностей, криптография и другие области
Теория графов	Теория игр, социология, логистика и другие области
Кодирование информации	Компьютерная наука, телекоммуникации и другие области

Множества и логические операции

Дискретная математика использует множества для представления объектов и операций над ними. Множество – это набор уникальных элементов. В дискретной математике множества могут использоваться для моделирования данных, например, множество студентов в классе или множество компьютерных программ.

Логические операции часто применяются в дискретной математике для манипуляций с множествами. Наиболее распространенными логическими операциями являются объединение, пересечение и разность множеств.

• Объединение множеств A и B обозначается как A ∪ B. Результат этой операции – множество, состоящее из всех элементов, которые входят в множество A или B (или в оба множества одновременно).
• Пересечение множеств A и B обозначается как A ∩ B. Результат этой операции – множество, состоящее из всех элементов, которые входят одновременно и в множество A, и в множество B.
• Разность множеств A и B обозначается как A \ B (или как A – B). Результат этой операции – множество, состоящее из всех элементов, которые входят в множество A, но не входят в множество B.

Также в дискретной математике часто используется отношение подмножества (A ⊆ B), которое означает, что все элементы множества A также являются элементами множества B. Это отношение может использоваться для проверки вложенности множеств и для построения иерархий объектов в различных областях знаний.

Особенности алгоритмов в дискретной математике

Алгоритмы в дискретной математике отличаются от алгоритмов в классической математике.

 

1. Важность точности
2. Необходимость работы с целыми числами
3. Работа с логическими значениями
4. Обработка больших объемов данных
5. Применение графов и деревьев

В дискретной математике работают с точностью до единицы, т.е. не используются дробные числа. Это вызвано тем, что в дискретной математике часто решают задачи, связанные с количеством объектов, а не с их весом или объемом.

Для решения задач в дискретной математике часто используются целые числа, т.к. они позволяют оперировать объектами в дискретных наборах. Это требуется, например, при определении количества возможных комбинаций.

Также, в дискретной математике часто используются логические значения. В задачах на логику и теорию алгоритмов, необходимо сравнивать и проверять условия, что требует использования логических операций.

Алгоритмы в дискретной математике часто работают с большими объемами данных. Вместо того, чтобы обрабатывать каждый элемент, используется алгоритм чтения из диапазона. Это помогает существенно ускорить работу алгоритма.

Графы и деревья являются важным инструментом в дискретной математике. Алгоритмы для работы с ними используются в различных областях, начиная от телекоммуникаций до комбинаторики.

Таким образом, алгоритмы в дискретной математике различаются от тех, которые применяются в классической математике. Специфика дискретной математики требует точности, работы с целыми числами, логическими значениями и большими объемами данных.

Алгоритмы и структуры данных

Алгоритм в дискретной математике — это последовательность логических и математических операций, выполняемых для решения конкретной задачи. Алгоритмы широко используются в программировании, математических расчетах, исследовании данных и многих других областях.

Структуры данных — это организация и хранение данных с учетом их использования в конкретном алгоритме. В отличие от классической математики, дискретная математика специализируется на работе с дискретными объектами, такими как последовательности, графы или множества. Поэтому, разработка эффективных структур данных является важной задачей в дискретной математике.

Примеры структур данных включают массивы, списки, деревья, хеш-таблицы, графы и многие другие. Использование правильной структуры данных может значительно ускорить работу с большими объемами данных и оптимизировать использование вычислительных ресурсов.

Другим важным аспектом в дискретной математике является оценка эффективности алгоритмов и структур данных. Для этого используется понятие сложности алгоритма, которая определяет количество ресурсов, необходимых для работы алгоритма в зависимости от размера входных данных.

В заключение, знание алгоритмов и структур данных является необходимым в современном мире программирования и вычислительных технологий. Оно позволяет разрабатывать устойчивые и производительные программы для обработки больших объемов данных и решения сложных задач.

Значимость теории графов в дискретной математике

Теория графов является одной из основных областей дискретной математики, которая занимается изучением связей между объектами, представленными в виде вершин и ребер. Она находит применение во многих областях, таких как теория алгоритмов, компьютерные сети, телекоммуникации, биоинформатика и другие.

В теории графов изучаются различные свойства графов, такие как связность, раскраски, планарность и другие. Эти свойства находят применение в решении многих задач, таких как поиск кратчайшего пути, планирование маршрутов, построение оптимальных расписаний и т.д.

Большое значение теория графов имеет в области информационных технологий, где она применяется для решения задач оптимизации и поиска. Например, она используется при проектировании алгоритмов маршрутизации в компьютерных сетях, оптимизации работы баз данных и т.д.

Также теория графов находит применение в биоинформатике, где ее используют для анализа генетических данных и определения связей между различными биологическими объектами.

Таким образом, теория графов имеет большое значение в дискретной математике и находит применение во многих областях науки и техники, где она помогает решать сложные задачи и оптимизировать работу различных систем.

Применение дискретной математики в криптографии

Криптография — это наука о методах защиты информации. Дискретная математика является одним из фундаментальных инструментов в криптографии. Она изучает дискретные структуры, такие как множества, графы и алгебраические системы, которые широко используются в криптографии.

Дискретная математика позволяет криптографам создавать надежные системы шифрования данных. Например, криптографические алгоритмы RSA и Эль-Гамаля основаны на дискретной математике и использовании простых чисел.

Дискретная математика также позволяет шифровать сообщения с помощью компьютера. Бинарные операции, такие как логические умножение и исключающее ИЛИ, используются для создания цифровых подписей и проверки целостности данных.

В целом, дискретная математика играет важную роль в криптографии и без нее разработка безопасных и надежных систем защиты информации не была бы возможной.

Применение дискретной математики в компьютерной науке

Дискретная математика играет важную роль в компьютерной науке и информатике. Она позволяет решать разнообразные задачи, связанные с обработкой данных и разработкой алгоритмов.

Одним из основных применений дискретной математики в компьютерной науке является разработка алгоритмов, которые обрабатывают данные на компьютере. Дискретная математика позволяет создавать эффективные алгоритмы, которые могут решать сложные задачи, например сортировку, поиск кратчайшего пути в графе или оптимизацию расписания.

Еще одним важным применением дискретной математики является теория информации, которая занимается изучением кодирования и передачи информации. С помощью дискретной математики можно разработать эффективные алгоритмы кодирования и декодирования, которые позволяют передать информацию с минимальными потерями.

Дискретная математика также используется в криптографии – науке о защите информации. С помощью дискретной математики можно разработать алгоритмы шифрования, которые обеспечивают надежную защиту данных.

Таким образом, дискретная математика играет важную роль в компьютерной науке и информатике, позволяя разрабатывать эффективные алгоритмы и обеспечивать защиту информации. Без использования дискретной математики современные компьютеры и сети были бы невозможными.

Применение дискретной математики в экономике и финансах

Дискретная математика находит широкое применение в экономике и финансах. Один из примеров – моделирование рынка ценных бумаг. При помощи дискретной математики можно анализировать и прогнозировать ценовые изменения акций и индексов.

Другой область применения дискретной математики – разработка систем принятия решений в экономике, основанных на теории игр и оптимизации. Например, можно использовать графы для построения моделей конкуренции на рынке или для определения оптимального портфеля инвестиций.

Дискретная математика также широко используется в области криптографии и безопасности информации. Алгоритмы шифрования и дешифрования основаны на методах дискретной математики, таких как теория чисел и теория графов.

В итоге, дискретная математика является важной составляющей в экономике и финансовой математике. Ее методы и техники помогают анализировать и оптимизировать деятельность фирм, моделировать рыночные процессы и разрабатывать надежные системы принятия решений.

Роль дискретной математики в искусственном интеллекте

Дискретная математика находит широкое применение в различных областях, включая исследование и разработку искусственного интеллекта. Ее роль заключается в предоставлении теоретических и практических инструментов для работы с абстрактными структурами данных и алгоритмами.

Одно из применений дискретной математики в искусственном интеллекте — это разработка и использование логических систем. Такие системы позволяют определять формальные правила, которые используются для принятия решений, моделирования проблем и выполнения других задач. Именно благодаря дискретной математике были разработаны такие формализмы, как исчисление высказываний, предикатное исчисление и исчисление резолюций.

Еще одной областью применения дискретной математики в искусственном интеллекте является теория графов. Она помогает решать задачи нахождения наиболее эффективного маршрута в навигационных системах, оптимизации процессов в сетях, классификации и кластеризации данных и многих других областях. Благодаря дискретной математике стали доступными такие алгоритмы, как алгоритм Дейкстры и алгоритмы поиска в глубину и в ширину.

Таким образом, дискретная математика играет важную роль в разработке и применении искусственного интеллекта. Она обеспечивает инструменты для работы с различными структурами данных и алгоритмами, что позволяет создавать эффективные и интересные решения для многих задач.

Математическая логика и рассуждения в дискретной математике

Математические логика и рассуждения являются основой дискретной математики. В отличие от классической математики, которая работает с непрерывными значениями и функциями, дискретная математика оперирует лишь с конечными или перечислимыми множествами.

В дискретной математике используются выразительные формальные языки для описания множеств, отношений и операций над ними. Эти языки обладают точно определенными правилами синтаксиса и семантики, которые позволяют строить математически корректные рассуждения и доказательства.

Кроме того, в дискретной математике широко применяются методы математической логики, включающие в себя теорию множеств, логику высказываний и предикатов, а также исчисление высказываний и предикатов. Эти методы позволяют формально описывать и анализировать различные структуры и системы, такие как компьютерные алгоритмы, сети связи, системы управления, базы данных и многие другие.

Важную роль в дискретной математике играют также графовые модели и теория игр. Они позволяют описывать и анализировать различные процессы, связанные с взаимодействиями и зависимостями между объектами, а также различные стратегии принятия решений и оптимизации деятельности.

В целом, математическая логика и рассуждения представляют собой универсальный инструмент, используемый в дискретной математике для формализации и анализа различных систем и процессов. Их применение позволяет выявлять скрытые закономерности и структуры, оптимизировать деятельность и принимать обоснованные решения.

Исследования и перспективы развития дискретной математики

Дискретная математика — это раздел математики, который изучает дискретные структуры, такие как графы, комбинаторика и теория чисел. В настоящее время дискретная математика имеет огромную значимость в компьютерной науке и информатике. Она является фундаментальным инструментом для создания алгоритмов, программного обеспечения и систем.

Современные исследования в области дискретной математики применяются в различных областях, таких как криптография, биология, экономика и многих других. Благодаря развитию информационных технологий, дискретная математика становится все более востребованной как теоретическая, так и прикладная наука.

Среди перспективных направлений исследований в дискретной математике можно выделить разработку новых алгоритмов, теорию графов и сетей, теорию кодирования и перспективы применения квантовых вычислений. Кроме того, актуальными являются исследования в области математической логики, комбинаторных методов и теории вероятностей.

С учетом перспективности дискретной математики, ее исследования и применения будут продолжаться и развиваться в ближайшее время, что будет способствовать созданию новых научных открытий и технических решений в различных областях человеческой деятельности.

Вопрос-ответ:

Что такое дискретная математика и как она отличается от классической?

Дискретная математика занимается изучением дискретных объектов, таких как целые числа, графы, отношения и множества. В отличие от классической математики, которая работает с непрерывными объектами, дискретная математика используется для решения конкретных задач в компьютерных науках, криптографии, теории кодирования и других областях.

Какие конкретные задачи можно решить с помощью дискретной математики?

С помощью дискретной математики можно решать задачи в области компьютерных наук, такие как оптимизация алгоритмов, анализ и проектирование баз данных, теория графов, криптография и многое другое. Эти задачи невозможно решить с помощью классической математики, поскольку она работает с непрерывными объектами, а дискретная математика — с дискретными объектами.

Что такое графы и как они используются в дискретной математике?

Граф — это совокупность вершин и ребер, соединяющих их. Они используются в теории графов — одной из основных областей дискретной математики. С помощью графов можно моделировать и анализировать сложные сетевые структуры, такие как дорожные сети, социальные сети, компьютерные сети и т. д.

Какие алгоритмы можно оптимизировать с помощью дискретной математики?

С помощью дискретной математики можно оптимизировать алгоритмы поиска и сортировки, алгоритмы распознавания образов и многое другое. Например, алгоритм Дейкстры для поиска кратчайшего пути в графе можно оптимизировать с помощью дискретной математики, используя алгоритм Форда-Фалкерсона для поиска максимального потока в сети.

Как дискретная математика используется в криптографии?

Дискретная математика играет ключевую роль в криптографии, поскольку позволяет создавать надежные шифры и доказывать их прочность. Например, RSA — один из самых популярных шифров — основан на дискретной математике. Он использует принципы теории чисел и алгоритмы решения дискретных уравнений для создания надежного шифра.

Какие преимущества дискретной математики в сравнении с классической?

Одним из главных преимуществ дискретной математики является ее способность решать конкретные задачи в компьютерных науках, криптографии, теории кодирования и других областях. Кроме того, дискретная математика позволяет решить задачи, которые невозможно решить с помощью классической математики. Она также обладает более широкими приложениями в современных технологиях и имеет больший потенциал для развития.

Какие недостатки есть у дискретной математики?

Один из недостатков дискретной математики заключается в том, что она ограничивается только дискретными объектами, что не всегда применимо в реальной жизни. Кроме того, некоторые алгоритмы и методы, используемые в дискретной математике, чрезвычайно сложны и труднопонятны для непрофессионалов. Также, некоторые области дискретной математики могут иметь ограниченные применения в современных технологиях.