Что такое плоскость в математике 5 класс

Плоскость в математике 5 класса — это геометрическая фигура, которая не имеет толщины и состоит из бесконечного количества точек. В данной статье мы рассмотрим определение плоскости, ее свойства и примеры задач для понимания этого понятия.

Плоскость – это одно из фундаментальных понятий в математике, с которым знакомятся уже в начальной школе. В пятом классе ученики изучают понятие плоскости более подробно, узнают о ее свойствах и основных элементах.

Плоскость – это бесконечное плоское пространство, имеющее два измерения – длину и ширину. Она является пространственным объектом без объема. Плоскость можно представить себе как бесконечную плоскую поверхность, на которой можно проводить линии, строить фигуры и измерять расстояния.

Например:

Плоскость можно сравнить с листом бумаги, на котором можно рисовать различные фигуры. Если взять две точки на плоскости, то всегда можно провести через них прямую. А если взять три точки, то можно провести через них плоскость.

Плоскость имеет свои особенности и свойства, которые изучаются в математике. Ученики узнают, что плоскость не имеет начала и конца, она бесконечна во всех направлениях. Важным свойством плоскости является то, что на ней выполняются аксиомы Евклида, которые определяют отношения между точками, прямыми и фигурами.

Что такое плоскость в математике?

Плоскость можно представить как бесконечный лист бумаги или поверхность стола. Она расположена в трехмерном пространстве и не имеет границ. Плоскость может быть горизонтальной, вертикальной или наклонной. Горизонтальная плоскость расположена параллельно горизонту, вертикальная плоскость — перпендикулярно горизонту, а наклонная плоскость — под углом к горизонту.

Плоскость в математике используется для решения задач, связанных с геометрией, алгеброй и тригонометрией. Она является основным понятием в этих областях и обеспечивает возможность решения разнообразных задач и построения геометрических фигур.

Примеры плоскостей в математике:

• Горизонтальная плоскость, которая является параллельной земной поверхности.
• Вертикальная плоскость, которая является перпендикулярной земной поверхности.
• Плоскость, заданная уравнением вида ax + by + cz + d = 0, где a, b, c и d — коэффициенты.
• Плоскость, заданная двумя пересекающимися прямыми.
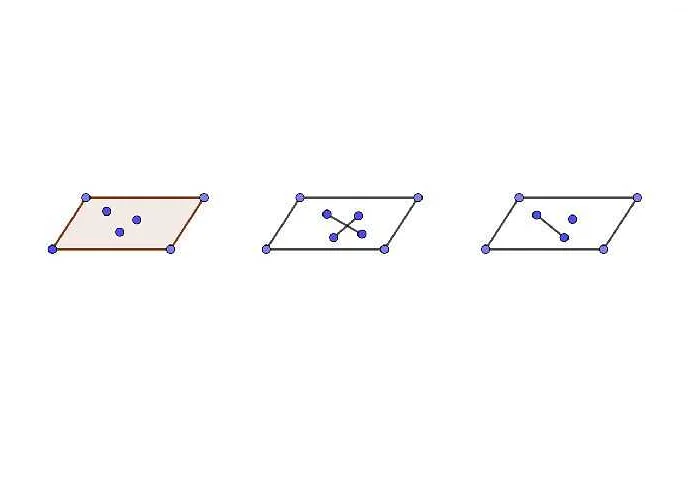
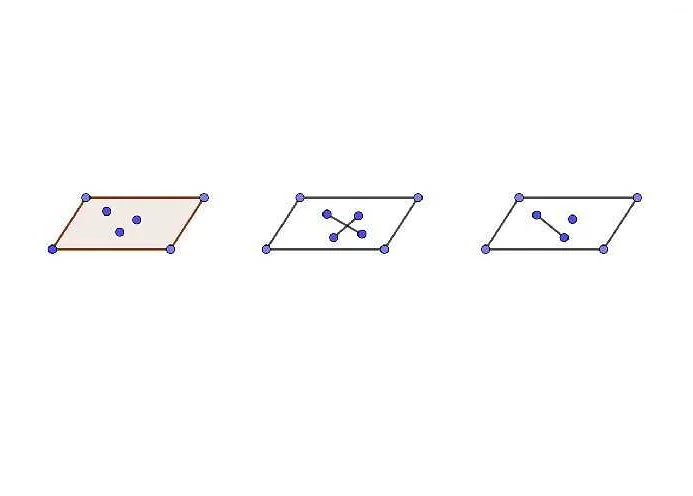
• Плоскость, заданная тремя точками, через которые она проходит.

Плоскость — важное понятие в геометрии и математике в целом. Она позволяет анализировать и решать разнообразные задачи, связанные с расположением и взаимодействием геометрических фигур и объектов.

Свойства плоскости

У плоскости есть ряд важных свойств:

СвойствоОписание

Прямые, параллельные плоскости	Если две плоскости не пересекаются, то все прямые, лежащие в одной плоскости и параллельные другой плоскости, также параллельны.
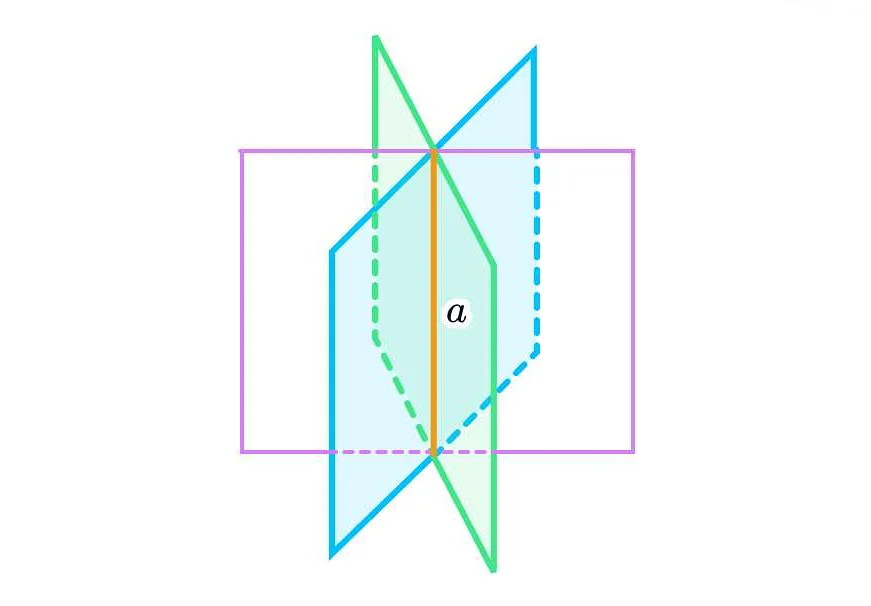
Точка пересечения плоскостей	Если две плоскости пересекаются, то общая точка пересечения является точкой принадлежности обеим плоскостям.
Свойство трех точек	Три точки, не лежащие на одной прямой, определяют плоскость. Иными словами, через любые три точки можно провести плоскость.
Координатное представление плоскости	Плоскость может быть описана с помощью уравнения вида Ax + By + Cz + D = 0, где A, B, C и D — коэффициенты, а x, y, z — координаты точки на плоскости.

Эти свойства плоскости играют важную роль в геометрии и математике в целом. Они позволяют анализировать и решать различные задачи, связанные с плоскостью, например, находить уравнения прямых, проведенных в плоскости, определять пересечения плоскостей и многое другое.

Основные элементы плоскости

Основными элементами плоскости являются:

Прямая	Прямая — это линия, которая не имеет ни начала, ни конца. Прямая может быть горизонтальной, вертикальной или наклонной.
Угол	Угол — это область плоскости, ограниченная двумя лучами, которые имеют общее начало. Угол измеряется в градусах и может быть острый, прямой или тупой.
Отрезок	Отрезок — это часть прямой, ограниченная двумя точками. Концы отрезка называются его концевыми точками.
Фигура	Фигура — это геометрическая форма, образованная прямыми, углами, отрезками и другими элементами плоскости.

Понимание основных элементов плоскости позволяет строить и анализировать геометрические фигуры, решать задачи и применять математические знания на практике.

Примеры использования плоскости

1. Геометрия: в геометрии плоскость используется для изучения фигур и пространственных объектов. На плоскости можно строить геометрические фигуры, решать задачи по нахождению площадей и периметров, а также проводить различные геометрические построения.

2. Картография: плоскость используется в картографии для создания карт и планов. На плоскости отображаются различные объекты и их расположение, позволяя нам ориентироваться на местности и находить нужные точки.

3. Архитектура и дизайн: плоскость используется в архитектуре и дизайне для создания планов зданий, мебели и других объектов. Архитекторы и дизайнеры используют плоскость для разработки проектов и визуализации идей.

4. Физика: плоскость используется в физике для изучения движения тел и векторов. На плоскости можно представить графики зависимостей различных физических величин, а также рассчитывать различные физические задачи.

5. Инженерия: плоскость используется в инженерии для разработки и проектирования различных систем и механизмов. Инженеры используют плоскость для создания чертежей и моделей, а также для анализа и расчета различных параметров.

Таким образом, плоскость является важным инструментом в разных областях науки и техники. Понимание ее свойств и возможностей помогает решать различные задачи и создавать новые инновационные решения.

Плоскость в геометрии

Плоскость можно представить как бесконечный плоский лист, на котором можно рисовать геометрические фигуры. Все точки на этом листе лежат в одной плоскости и образуют плоскую поверхность.

Плоскость в геометрии играет важную роль. Она является базовым понятием, на котором строится большинство геометрических фигур и пространственных объектов. Например, треугольник — это фигура, образованная трёмя точками, которые лежат на одной плоскости.

Примеры плоскостей в повседневной жизни:

• Стол — это плоская поверхность, на которой можно разместить предметы.
• Земля — плоскость, на которой мы живем.
• Экран компьютера — плоскость, на которой отображается информация.

Плоскость в геометрии имеет свои особенности и свойства, среди которых:

1. Прямая, проходящая через любые две точки на плоскости, также лежит в этой плоскости.
2. Две параллельные прямые никогда не пересекаются на плоскости.
3. На плоскости можно построить разнообразные геометрические фигуры, такие как треугольники, квадраты, окружности и т. д.

Таким образом, плоскость — это важное понятие в геометрии, которое позволяет анализировать и строить геометрические фигуры и пространственные объекты.

Плоскость в тригонометрии

Каждая точка на плоскости имеет координаты, которые обозначаются парой чисел (x, y). Координата x отображает расстояние точки от вертикальной оси, а координата y – расстояние точки от горизонтальной оси. Таким образом, плоскость может быть использована для представления различных геометрических объектов и функций, связанных с углами.

В тригонометрии функции углов, такие как синус, косинус и тангенс, определяются на плоскости. Например, синус угла α – это отношение длины противолежащего катета к длине гипотенузы в прямоугольном треугольнике, а косинус – отношение длины прилежащего катета к длине гипотенузы.

Таким образом, плоскость в тригонометрии играет важную роль в изучении геометрических свойств углов и функций, связанных с ними. Она позволяет наглядно представить геометрические объекты и упрощает вычисления и анализ тригонометрических функций.

Плоскость в алгебре

Уравнение плоскости имеет вид Ax + By + Cz + D = 0, где A, B, C — коэффициенты, определяющие направление нормали к плоскости, а D — свободный член. Коэффициенты A, B и C задают вектор нормали (A, B, C).

Плоскость может быть определена также через точку и вектор нормали. Если дана точка P(x, y, z) и вектор нормали N(A, B, C), то уравнение плоскости может быть записано как (P — P0) * N = 0, где P0 — координаты точки P.

Пример:

• Уравнение плоскости 2x — 3y + 4z — 5 = 0 определяет плоскость в трехмерном пространстве.
• Если задана точка P(1, 2, 3) и вектор нормали N(2, -1, 3), то уравнение плоскости может быть записано как (P — (1, 2, 3)) * (2, -1, 3) = 0.

Плоскость в алгебре играет важную роль при решении систем линейных уравнений и в других математических задачах, связанных с алгеброй и геометрией.

Плоскость в физике

В физике понятие плоскости играет важную роль при изучении движения тел и взаимодействия физических явлений. Плоскость в физике может быть определена как идеализированная поверхность, которая не имеет толщины и ограничивает пространство.

Плоскость в физике может использоваться для моделирования различных физических процессов. Например, при изучении движения тела по плоскости можно использовать плоскость как базовую модель, на которой рассматривается движение тела без учета трения и влияния других факторов.

Плоскость также используется в физике для построения графиков и диаграмм, которые помогают визуализировать и анализировать различные физические явления. Например, на графике зависимости времени от расстояния можно представить движение тела по плоскости и определить его скорость и ускорение.

В физике плоскость может быть задана координатами или уравнением, которое связывает координаты точек на плоскости. Зная уравнение плоскости, можно определить, какие точки принадлежат плоскости и наоборот.

Итак, плоскость в физике является важным понятием, которое используется для моделирования и анализа различных физических явлений и процессов.

Видео по теме:

Что такое плоскость?

Плоскость — это геометрическая фигура, которая не имеет толщины и простирается бесконечно во всех направлениях.

Как определить плоскость?

Плоскость можно определить, задав две любые точки и вектор, параллельный плоскости.

Какие примеры плоскостей можно привести?

Примерами плоскостей могут служить поверхность стола, поверхность бассейна, поверхность листа бумаги.

Какие свойства имеет плоскость?

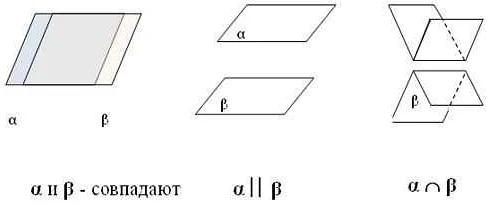
Плоскость имеет свойства, такие как параллельность прямых, перпендикулярность, совпадение с другой плоскостью и др.

Как можно провести прямую на плоскости?

Прямую на плоскости можно провести, задав две точки и соединив их прямой линией.

Какое определение плоскости в математике?

Плоскость в математике — это геометрическое понятие, обозначающее бесконечную плоскую поверхность, на которой лежат все точки пространства. Она не имеет толщины и неограничена во всех направлениях. Можно представить плоскость как невидимую поверхность, на которой можно нарисовать и измерить любую фигуру.