Что такое плоскость 5 класс математика

Плоскость в математике — это двумерное пространство, в котором все точки лежат на одной плоскости. Уроки математики для 5 класса включают изучение основных понятий и свойств плоскости, таких как прямые, отрезки, углы и фигуры. Узнайте больше о плоскости и ее применении в школьной программе математики для 5 класса.

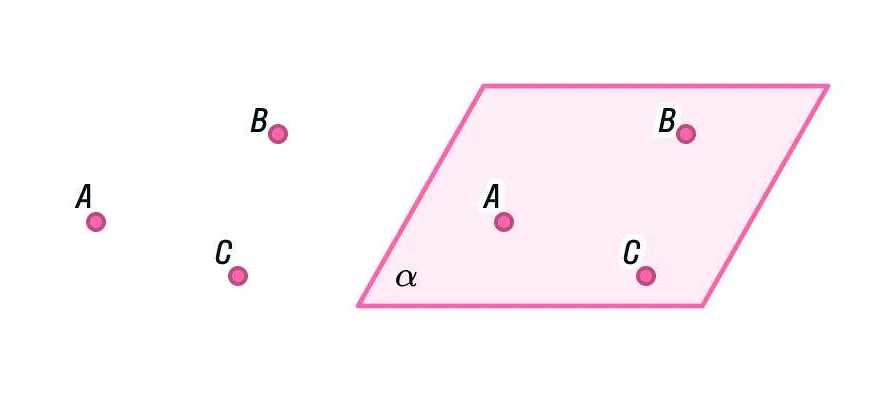
Плоскость — это одномерное пространство, которое не имеет толщины. В математике плоскость является одним из основных объектов изучения геометрии. Она представляет собой бесконечную поверхность, состоящую из точек, которые лежат на одной и той же плоскости.

Важным понятием, связанным с плоскостью, является прямая. Прямая — это самый простой геометрический объект, который представляет собой бесконечный набор точек, расположенных на одной линии. Прямая может лежать в плоскости или быть параллельной плоскости.

Свойства плоскости:

• Плоскость можно задать двумя независимыми направлениями, которые называются осями плоскости.
• На плоскости можно измерять расстояние между точками или длину отрезков.
• Плоскость имеет бесконечное количество прямых, лежащих на ней.
• Прямая, лежащая в плоскости, может пересекать плоскость в одной или нескольких точках.
• Если две прямые не пересекаются ни в одной точке и лежат в одной плоскости, то они называются параллельными.

Изучение плоскости и ее свойств помогает развивать пространственное воображение и логическое мышление. Понимание плоскости и прямой является важной основой для дальнейшего изучения геометрии и других математических дисциплин.

Что такое плоскость?

Плоскость может быть представлена в виде бесконечной бумаги или экрана, на котором можно рисовать и делать различные геометрические построения.

Основные свойства плоскости:

• Плоскость не имеет границ и простирается во все стороны.
• На плоскости можно проводить прямые линии, окружности, многоугольники и другие геометрические фигуры.
• Любые две точки на плоскости можно соединить прямой линией.
• Плоскость делится на две половины бесконечным количеством прямых линий, называемых перпендикулярами.
• На плоскости можно измерять расстояния и углы.

Плоскость — это одно из основных понятий геометрии, которое используется для изучения различных фигур и их свойств. Понимание плоскости помогает решать задачи и строить точные геометрические построения.

Понятие плоскости в математике

Основные свойства плоскости:

• Плоскость не имеет начала и конца, она бесконечна во всех направлениях.
• Любые две точки на плоскости можно соединить прямой линией, которая лежит полностью на плоскости.
• Все прямые, пересекающиеся на плоскости, лежат полностью на этой плоскости.
• Плоскость может быть наклонной, горизонтальной или вертикальной.

Плоскость широко используется в математике для решения задач и построения фигур. Она является одним из основных понятий геометрии и имеет множество применений в других областях науки и техники.

Основные свойства плоскости

Свойство 1: Любые три точки, не лежащие на одной прямой, определяют плоскость. Это значит, что если мы возьмем три точки и соединим их отрезками, то получим плоскость.

Свойство 2: На плоскости можно провести прямую и любой отрезок. Прямая — это набор точек, расположенных на одной линии. Отрезок — это часть прямой, ограниченная двумя точками.

Свойство 3: Всякая прямая, лежащая в плоскости, лежит целиком в этой плоскости. Это означает, что если прямая находится в плоскости, то все ее точки также находятся в этой плоскости.

Свойство 4: Любые две пересекающиеся прямые в плоскости определяют эту плоскость. Если две прямые пересекаются в точке и лежат в одной плоскости, то они определяют эту плоскость.

Свойство 5: Плоскость не имеет начала и конца, то есть она бесконечна во всех направлениях. Мы всегда можем продолжить плоскость в любую сторону.

Эти основные свойства плоскости помогают нам изучать и понимать ее характеристики и взаимодействие с другими геометрическими фигурами.

Плоскость и ее элементы

В плоскости можно выделить несколько основных элементов:

1. Прямая — это рисунок, который можно нарисовать на плоскости без поднятия карандаша. Прямая имеет бесконечную длину и ширину и состоит из бесконечного числа точек.
2. Угол — это область плоскости, образованная двумя лучами с общим началом. Угол измеряется в градусах или радианах и может быть острый, прямой, тупой или полный.
3. Треугольник — это фигура, состоящая из трех линий, которые соединяют три точки. Треугольник имеет три стороны, три угла и три вершины.
4. Прямоугольник — это четырехугольник, у которого все углы прямые. Прямоугольник имеет две параллельные стороны и четыре прямых угла.
5. Круг — это фигура, все точки которой находятся на одинаковом расстоянии от центра. Круг имеет радиус, диаметр и длину окружности.

Плоскость и ее элементы играют важную роль в геометрии и математике в целом. Изучение плоскости позволяет решать различные задачи и строить сложные конструкции.

Уравнение плоскости

Плоскость в математике может быть определена с помощью уравнения плоскости. Уравнение плоскости представляет собой линейное уравнение, которое задает все точки данной плоскости.

Уравнение плоскости имеет следующий вид:

Ax + By + Cz + D = 0

Здесь A, B и C — коэффициенты, определяющие нормальный вектор плоскости, а D — свободный член.

Нормальный вектор плоскости — это вектор, перпендикулярный плоскости. Он может быть найден с помощью коэффициентов A, B и C уравнения плоскости.

Если даны три точки на плоскости (x1, y1, z1), (x2, y2, z2) и (x3, y3, z3), то уравнение плоскости можно найти, используя формулу:

(x — x1)(y2 — y1)(z3 — z1) — (x2 — x1)(y — y1)(z3 — z1) + (x2 — x1)(y3 — y1)(z — z1) — (x3 — x1)(y2 — y1)(z — z1) = 0

Уравнение плоскости полностью определяет их геометрические свойства и позволяет решать задачи, связанные с плоскостью в математике.

Пересечение плоскостей

Если две плоскости пересекаются по точке, то можно сказать, что они имеют общую точку пересечения. Общая точка пересечения двух плоскостей может быть единственной или бесконечным множеством точек.

Если две плоскости пересекаются по прямой, то можно сказать, что они имеют общую прямую пересечения. Общая прямая пересечения двух плоскостей также может быть единственной или бесконечным множеством прямых.

Если две плоскости не имеют общих точек или общих прямых пересечения, то их пересечение является пустым множеством. Такие плоскости называются параллельными.

Пересечение плоскостей является важным понятием в геометрии. Оно позволяет решать задачи, связанные с различными пространственными конструкциями, например, находить общие точки или прямые, скрещивать линии и плоскости.

Параллельные плоскости

Основное свойство параллельных плоскостей заключается в том, что все прямые, лежащие в одной плоскости и перпендикулярные к другой плоскости, будут параллельны.

Чтобы найти параллельные плоскости, достаточно взять любую плоскость и сдвинуть ее вдоль одной из осей координат без поворота. Таким образом, мы получим бесконечное множество плоскостей, параллельных исходной.

Также можно задать параллельные плоскости с помощью уравнения. Если плоскость задана уравнением Ax + By + Cz + D = 0, то параллельная плоскость будет иметь уравнение Ax + By + Cz + D’ = 0, где D’ — новый коэффициент сдвига по оси Z.

Параллельные плоскости имеют множество приложений в геометрии, физике и других науках. Например, они используются для построения параллелепипедов, плоских зеркал, и для описания траекторий движения объектов в пространстве.

Свойства параллельных плоскостей

Не пересекаются и не скрещиваются

Все прямые, перпендикулярные одной плоскости и лежащие в другой плоскости, параллельны

Можно задать уравнением

Имеют множество приложений в геометрии и физике

Видео по теме:

Вопрос-ответ:

Как определить плоскость?

Плоскость определяется как геометрическое пространство, состоящее из бесконечного количества точек и не имеющее толщины. Она распространяется во всех направлениях и может быть представлена как бесконечная плоскость.

Какие основные понятия связаны с плоскостью?

Основные понятия, связанные с плоскостью, включаются такие как точка, прямая, угол. Точка — это базовый элемент плоскости, прямая — это множество точек, лежащих на одной плоскости, а угол — это область между двумя лучами, которые имеют общее начало и лежат в одной плоскости.

Какие свойства имеет плоскость?

Плоскость имеет несколько свойств. Во-первых, она не имеет толщины, а значит не может быть измерена в третьем измерении. Во-вторых, для любых двух точек, лежащих на плоскости, можно провести прямую, которая будет лежать полностью в этой плоскости. И в-третьих, две пересекающиеся прямые на плоскости будут пересекаться в одной точке.

Какие примеры плоскостей можно привести?

Примерами плоскостей могут быть поверхность стола, поверхность бумаги, поверхность земли и т.д. Эти поверхности можно рассматривать как плоскости, так как они не имеют толщины и распространяются во всех направлениях.

Как плоскость используется в повседневной жизни?

Плоскость используется в повседневной жизни во многих областях. Например, в архитектуре и строительстве плоскость используется для создания планов зданий. В графическом дизайне и искусстве плоскость используется для создания изображений. Также плоскость используется в географии для изображения карт.

Что такое плоскость?

Плоскость — это геометрическое понятие, которое представляет собой бесконечную плоскую поверхность, не имеющую толщины и простирающуюся во все стороны.

Наклонные плоскости

Наклонные плоскости часто встречаются в реальном мире, например, крыши домов, наклонные поверхности на улицах, склоны гор и т.д. Математически, наклонные плоскости могут быть заданы уравнением вида: Ax + By + Cz + D = 0, где A, B и C – коэффициенты, определяющие направление наклона плоскости, а D – свободный член, определяющий положение плоскости относительно начала координат.

Для наглядности и удобства работы с наклонными плоскостями, их часто представляют в виде таблицы, где указываются координаты нескольких точек, принадлежащих этой плоскости. Такая таблица позволяет увидеть, как плоскость наклоняется относительно осей координат и установить взаимосвязь между направлением наклона и значениями коэффициентов A, B и C.

Точкаxyz

Точка A	1	2	3
Точка B	4	5	6
Точка C	7	8	9

В приведенной таблице указаны координаты трех точек – A, B и C, принадлежащих некоторой наклонной плоскости. Используя эти данные, можно определить уравнение плоскости и выяснить, как она наклоняется относительно осей координат.

Плоскость в пространстве

В отличие от плоскости на плоском поле, плоскость в пространстве имеет тримерную форму и может быть представлена как бесконечное расширение на все стороны. Она не имеет конкретных границ и может протягиваться во всех направлениях.

Плоскость характеризуется двумя основными свойствами: она является геометрической фигурой без толщины и имеет бесконечные размеры. Все точки на плоскости находятся на одинаковом расстоянии от нее и полностью определяют ее положение и форму.

В математике плоскость в пространстве обычно обозначается буквой «П» или рисуется с помощью параллельных линий. Она широко используется в геометрии, анализе, физике и других науках для изучения пространственных отношений и моделирования различных объектов.