Правила по математике как найти скорость время и расстояние

В этой статье рассматриваются основные правила математики для вычисления скорости, времени и расстояния. Вы узнаете, как использовать эти правила для решения различных задач и получения точных результатов. Научитесь применять формулы и просчитывать различные варианты расчетов в разных ситуациях. Будут представлены практические примеры и пошаговые инструкции для решения задач по математике на скорость, время и расстояние.

Математика является одной из важнейших наук, которая применяется во многих сферах нашей жизни. Особенно важным является правильное использование математических формул и правил при решении различных задач. В данной статье мы поговорим о том, как можно определить скорость, время и расстояние, используя простые математические формулы.

Скорость — это величина, которая показывает, как быстро объект движется относительно других объектов. Для определения скорости необходимо знать расстояние, которое объект преодолел, и время, за которое он это сделал. Формула для вычисления скорости выглядит следующим образом: скорость = расстояние / время.

Время — это интервал, за который происходит перемещение объекта. Для определения времени нужно знать расстояние, которое объект преодолел, и скорость, с которой он двигался. Формула для вычисления времени выглядит так: время = расстояние / скорость.

Расстояние — это протяженность между двумя точками. Для определения расстояния нужно знать скорость, с которой двигается объект, и время, за которое он двигается. Формула для вычисления расстояния выглядит следующим образом: расстояние = скорость * время.

Запомните эти простые формулы и правила, и вы сможете легко решать задачи, связанные с определением скорости, времени и расстояния.

Основные понятия в математике

1. Число — основное понятие математики. Числа могут быть натуральными (1, 2, 3…), целыми (-3, -2, -1, 0, 1, 2, 3…), рациональными (дроби) и иррациональными (например, корень из 2).

2. Операции — математические действия, которые выполняются над числами. Основные операции включают сложение, вычитание, умножение и деление. Операции могут также включать в себя возведение в степень, извлечение корня и другие.

3. Формула — математическое выражение, которое описывает отношение между различными величинами. Формулы могут быть использованы для решения уравнений и предсказания значений.

4. Переменная — символ, который представляет неизвестное значение в математическом выражении или уравнении. Переменные могут принимать различные значения и использоваться для обозначения неизвестных величин.

5. Уравнение — математическое выражение, в котором две величины считаются равными. Решение уравнения — это значение переменной, при котором обе части уравнения равны.

6. График — визуальное представление математической функции или зависимости между переменными. Графики могут быть использованы для анализа и представления данных.

7. Пропорция — математическое соотношение между двумя величинами. Пропорциональность может быть выражена с помощью уравнения или графика.

Эти основные понятия являются основой для решения различных математических задач и позволяют лучше понимать мир вокруг нас.

Скорость

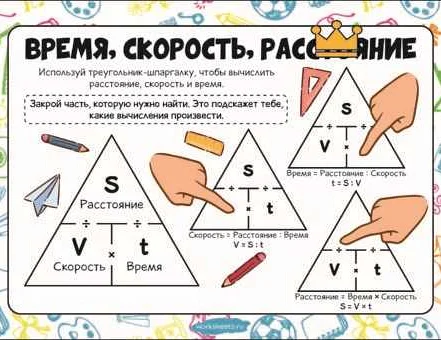
Скорость можно вычислить, разделив пройденное расстояние на затраченное время:

Скорость = Расстояние / Время

Единицы измерения скорости могут быть различными, например:

• метры в секунду (м/с)
• километры в час (км/ч)
• мили в час (ми/ч)

Чтобы рассчитать скорость, необходимо знать какое расстояние было пройдено и за какое время.

Скорость является важной физической величиной и используется в различных областях, таких как автомобильная промышленность, спорт, физика и многое другое.

Формула времени

Формула времени имеет следующий вид:

Время (t) = Расстояние (d) / Скорость (v)

В этой формуле время (t) вычисляется путем деления расстояния (d) на скорость (v).

Например, если известно, что автомобиль движется со скоростью 60 км/ч и нужно вычислить время, за которое он пройдет расстояние в 120 километров, можно воспользоваться формулой времени:

Время (t) = 120 км / 60 км/ч = 2 часа

Таким образом, автомобиль пройдет расстояние в 120 километров за 2 часа.

Формула расстояния

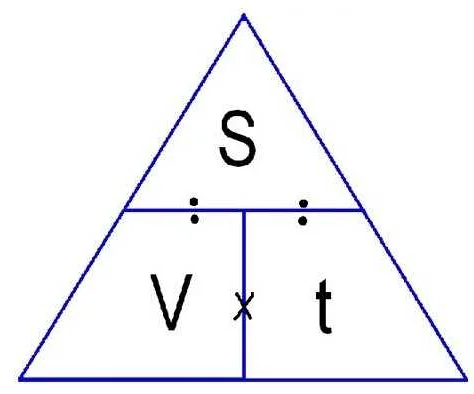
Формула расстояния выглядит следующим образом:

расстояние = скорость * время

Такая формула позволяет найти расстояние, которое проходит объект, двигаясь с определенной скоростью в течение определенного времени. Например, если автомобиль движется со скоростью 60 километров в час в течение 2 часов, то расстояние, которое он пройдет, можно найти, умножив скорость на время: 60 км/ч * 2 ч = 120 километров.

Формула расстояния является важным инструментом в решении множества задач по математике, физике и других науках. Она позволяет определить, сколько объект пройдет путь за определенное время, и может быть использована для решения различных практических задач.

Как найти скорость?

Скорость можно найти, разделив пройденное расстояние на затраченное время. Формула для вычисления скорости выглядит следующим образом:

Скорость = Расстояние / Время

Пример: Если объект преодолел расстояние 200 метров за 10 секунд, то его скорость будет равна:

Скорость = 200 м / 10 с = 20 м/с

Очень важно помнить, что скорость имеет направление. Если объект движется вперед, скорость будет положительной. Если объект движется назад, скорость будет отрицательной.

Также стоит отметить, что скорость может быть постоянной или изменяться со временем. При постоянной скорости объект движется с одинаковой скоростью на протяжении всего пути. При изменяющейся скорости объект может двигаться быстрее или медленнее в разные моменты времени.

В заключение, чтобы найти скорость, нужно знать расстояние, которое преодолел объект, и время, за которое он это сделал. Разделив эти два значения, можно получить скорость объекта.

Как найти время?

Для вычисления времени в математике необходимо знать расстояние и скорость движения.

Формула для расчета времени: время = расстояние / скорость.

Время измеряется в единицах, соответствующих системе измерения расстояния и скорости. Например, если расстояние измеряется в километрах, а скорость в километрах в час, то время будет выражаться в часах.

Для применения формулы необходимо знать значения расстояния и скорости. Расстояние можно измерить на карте или с помощью других средств измерения, а скорость обычно известна или может быть определена экспериментально.

Важно помнить, что время не может быть отрицательным значением. Если расстояние и скорость выбраны таким образом, что время получается отрицательным, это может означать, что формула была применена неправильно или что данные некорректны.

Также стоит учитывать, что формула для вычисления времени является простой моделью и не учитывает другие факторы, такие как ускорение или замедление движения, препятствия на пути и т.д. Поэтому результаты вычислений времени могут отличаться от реальных значений в реальных условиях.

В любом случае, вычисление времени по формуле помогает получить представление о временных характеристиках движения и может быть полезно для планирования и анализа различных ситуаций.

Как найти расстояние?

Для нахождения расстояния в математике необходимо знать скорость и время, за которое произошло движение. Формула для вычисления расстояния выглядит следующим образом:

Расстояние = Скорость × Время

Чтобы найти расстояние, нужно умножить значение скорости на время движения. Например, если скорость равна 60 километров в час, а время движения составляет 2 часа, то расстояние будет равно 120 километрам.

Также существует другая формула для вычисления расстояния, когда известны начальная и конечная точки движения:

Расстояние = Конечная точка — Начальная точка

Эта формула применяется, когда требуется определить расстояние между двумя точками на плоскости или на графике. Например, если начальная точка имеет координаты (3, 4), а конечная точка имеет координаты (8, 9), то расстояние между ними будет равно 5.

Таким образом, чтобы найти расстояние, необходимо знать либо скорость и время, либо начальную и конечную точки движения, и использовать соответствующую формулу для расчета.

Примеры задач с решениями

Ниже приведены примеры задач по математике, связанные с расчетом скорости, времени и расстояния, а также их решения.

1. Задача 1:

   Автомобиль движется со скоростью 60 км/ч. Найдите время, за которое автомобиль преодолеет расстояние в 300 км.

   Решение:

   Для решения данной задачи используем формулу:

   Время = Расстояние / Скорость

   Подставляем значения:

   Время = 300 км / 60 км/ч = 5 ч

   Ответ: Автомобиль преодолеет расстояние в 300 км за 5 часов.

2. Задача 2:

   Велосипедист едет со скоростью 20 км/ч. За какое время он преодолеет расстояние в 80 км?

   Решение:

   Используем формулу:

   Время = Расстояние / Скорость

   Подставляем значения:

   Время = 80 км / 20 км/ч = 4 ч

   Ответ: Велосипедист преодолеет расстояние в 80 км за 4 часа.

3. Задача 3:

   Поезд движется со скоростью 90 км/ч. Если он преодолеет расстояние в 540 км, сколько времени это займет?

   Решение:

   Используем формулу:

   Время = Расстояние / Скорость

   Подставляем значения:

   Время = 540 км / 90 км/ч = 6 ч

   Ответ: Поезд преодолеет расстояние в 540 км за 6 часов.

Советы для успешного решения задач

Решение математических задач, связанных с определением скорости, времени и расстояния, может быть сложным, особенно для начинающих. Однако, следуя некоторым советам, вы сможете справиться с ними проще и быстрее.

1. Внимательно ознакомьтесь с формулой. Перед тем, как приступить к решению задачи, убедитесь, что вы понимаете, как применить соответствующую формулу. Запишите ее на бумаге или в уме, чтобы иметь представление о том, какие данные вам понадобятся.

2. Четко определите известные и неизвестные значения. Разделите данные из условия задачи на известные и неизвестные значения. Запишите их отдельно, чтобы у вас был ясный обзор всей информации.

3. Используйте единицы измерения. Обращайте внимание на единицы измерения, которые используются в задаче. Убедитесь, что все значения имеют одинаковую систему измерения. Если необходимо, конвертируйте их в одну систему для удобства решения.

4. Применяйте подход «выражение-решение». В большинстве задач, связанных с скоростью, временем и расстоянием, можно использовать подход «выражение-решение». Составьте уравнение, используя соответствующую формулу, и выразите неизвестное значение через известные. Затем решите полученное уравнение, чтобы найти ответ.

5. Не забывайте о правилах арифметики. При решении задач по математике всегда придерживайтесь правил арифметики. Выполняйте операции последовательно и аккуратно, чтобы избежать ошибок в вычислениях.

6. Проверьте свой ответ. После того, как вы получили ответ, проверьте его на соответствие условию задачи. Убедитесь, что ваше решение логически верно и имеет смысл с точки зрения физики и математики.

Следуя этим советам, вы сможете успешно решать задачи, связанные с определением скорости, времени и расстояния. Практика и упорство помогут вам улучшить свои навыки и стать более уверенным в решении подобных задач.

Вопрос-ответ:

Как вычислить скорость, если известно время и расстояние?

Чтобы вычислить скорость, если известны время и расстояние, нужно разделить расстояние на время. Формула выглядит следующим образом: скорость = расстояние / время.

Как вычислить время, если известна скорость и расстояние?

Чтобы вычислить время, если известны скорость и расстояние, нужно разделить расстояние на скорость. Формула выглядит следующим образом: время = расстояние / скорость.

Как вычислить расстояние, если известны скорость и время?

Чтобы вычислить расстояние, если известны скорость и время, нужно умножить скорость на время. Формула выглядит следующим образом: расстояние = скорость * время.

Какие единицы измерения используются для скорости, времени и расстояния?

Для скорости можно использовать единицы измерения, такие как километры в час (км/ч), метры в секунду (м/с) или мили в час (ми/ч). Для времени используются единицы измерения, такие как секунды (с), минуты (мин) или часы (ч). Для расстояния можно использовать единицы измерения, такие как километры (км), метры (м) или мили (ми).

Могут ли правила по математике использоваться для вычисления скорости, времени и расстояния в разных ситуациях?

Да, правила по математике для вычисления скорости, времени и расстояния применимы в разных ситуациях. Например, можно использовать эти правила для определения скорости движения автомобиля, времени путешествия или расстояния между двумя городами. Они являются универсальными и могут быть применены во многих областях.

Какая формула позволяет вычислить скорость?

Формула для вычисления скорости: скорость равна расстоянию, разделенному на время. То есть, V = D / T, где V — скорость, D — расстояние и T — время.

Видео по теме: