Что такое прием гаусса 5 класс математика

Прием гаусса в математике для 5 класса — это метод решения систем линейных уравнений, разработанный немецким математиком Карлом Фридрихом Гауссом. Ученикам пятого класса данный прием помогает решать задачи по алгебре и находить неизвестные значения переменных. Узнайте, как использовать прием гаусса в математике и как он помогает в решении уравнений и задач.

Прием Гаусса — это эффективный метод решения арифметических задач, который был разработан известным немецким математиком Карлом Фридрихом Гауссом. Этот метод позволяет сократить время решения задач и сделать математику более доступной и понятной для учащихся.

Основная идея приема Гаусса заключается в том, чтобы сократить сложные вычисления путем нахождения закономерностей и использования простых арифметических операций. Для этого необходимо разбить сложную задачу на несколько простых и применить соответствующие математические действия.

Например, при решении задачи на сложение чисел от 1 до 100, можно заметить, что первое и последнее число в сумме дадут 101, второе и предпоследнее — 101 и так далее. Таким образом, получится 50 пар чисел, каждая из которых дает сумму 101. Для нахождения итоговой суммы нужно умножить 101 на 50, что дает результат 5050.

При использовании приема Гаусса важно уметь выявлять закономерности и применять их в арифметических задачах. Это поможет ученикам более эффективно решать задачи и развивать математическое мышление.

Прием Гаусса: что это такое?

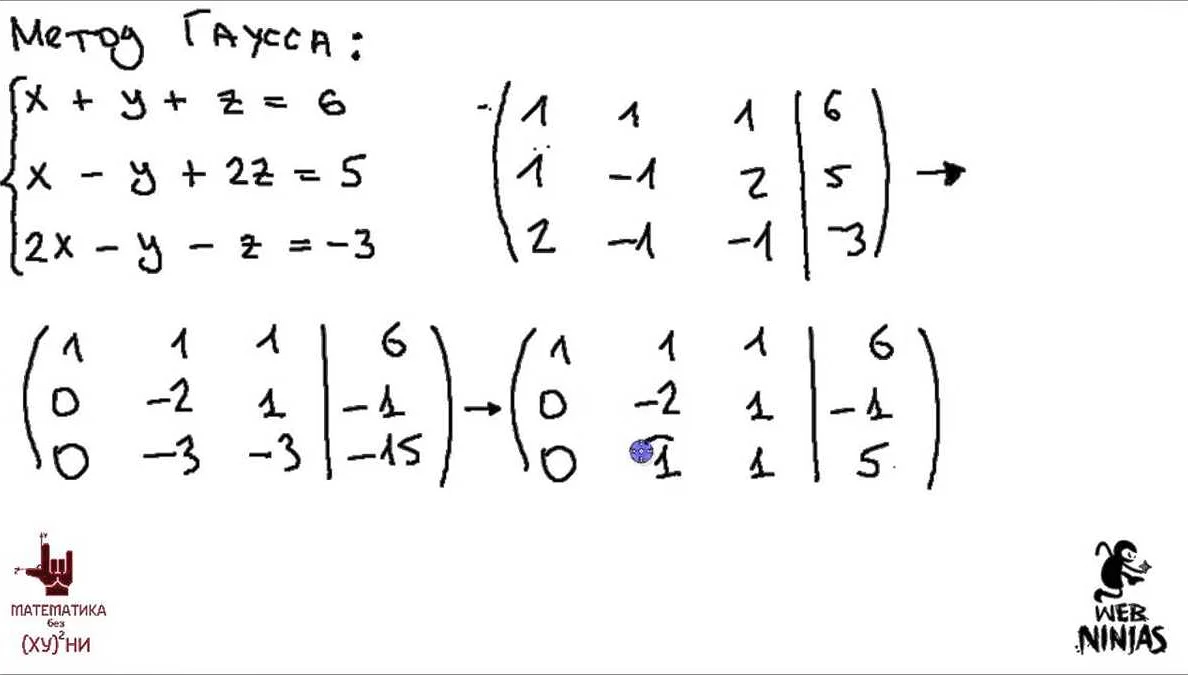
Основная идея приема Гаусса заключается в том, чтобы найти закономерность в числах или операциях, которую можно использовать для упрощения вычислений. Для этого необходимо внимательно изучить условие задачи и найти связь между числами или операциями.

Проиллюстрируем прием Гаусса на конкретном примере. Предположим, у нас есть задача: «Сколько будет 1 + 2 + 3 + … + 100?». На первый взгляд, может показаться, что нужно сложить все числа от 1 до 100, что займет много времени и может быть довольно сложно. Но с помощью приема Гаусса мы можем найти ответ быстро и легко.

Для этого мы можем воспользоваться формулой суммы арифметической прогрессии, которая выглядит следующим образом: Сумма = (первый элемент + последний элемент) * количество элементов / 2. В нашем случае, первый элемент равен 1, последний элемент равен 100, количество элементов равно 100. Подставляя эти значения в формулу, получаем:

Первый элементПоследний элементКоличество элементовСумма

1

100

100

(1 + 100) * 100 / 2 = 5050

Таким образом, сумма чисел от 1 до 100 будет равна 5050. Этот пример наглядно демонстрирует, как прием Гаусса позволяет решать сложные арифметические задачи быстро и эффективно, используя простые математические законы и формулы.

Прием Гаусса может быть использован не только для задач на сложение, но и для других арифметических операций, таких как вычитание, умножение и деление. Главное — найти закономерность или формулу, которая позволит упростить вычисления и найти ответ на задачу.

Видео по теме:

Основные понятия

Основными понятиями в приеме Гаусса являются:

1. Система линейных уравнений – это набор уравнений, содержащих неизвестные переменные и образующих единую систему. Например, система линейных уравнений может выглядеть следующим образом:

a11x1 + a12x2 + … + a1nxn = b1

a21x1 + a22x2 + … + a2nxn = b2

…

am1x1 + am2x2 + … + amnxn = bm

1. Коэффициенты – это числа, стоящие перед неизвестными переменными в каждом уравнении системы. Обозначаются символами aij, где i – номер уравнения, j – номер переменной.
2. Неизвестные переменные – это значения, которые мы ищем и обозначаем символами xi, где i – номер переменной.
3. Свободные члены – это значения, которые стоят в правой части уравнений системы и обозначаются символами bi, где i – номер уравнения.

Задача приема Гаусса состоит в том, чтобы привести систему линейных уравнений к такому виду, чтобы в каждом уравнении неизвестные переменные стояли только с одной стороны равенства, а коэффициенты перед ними были равны единице или нулю. Затем, используя методы элементарных преобразований, система уравнений приводится к треугольному виду или к упрощенной системе, которую можно решить методом обратного хода.

Метод Гаусса в математике

Главная идея метода Гаусса заключается в пошаговом приведении системы линейных уравнений к эквивалентной системе, в которой каждое уравнение содержит только одну неизвестную. Для этого применяются элементарные преобразования, такие как сложение/вычитание уравнений, умножение/деление уравнений на ненулевые числа и перестановка уравнений местами.

Процесс решения системы линейных уравнений методом Гаусса включает следующие шаги:

1. Запись системы уравнений в матричной форме.
2. Приведение матрицы системы к треугольному виду путем элементарных преобразований.
3. Обратный ход, при котором из треугольной матрицы получается диагональная матрица.
4. Вычисление значений неизвестных по полученной диагональной матрице.

Метод Гаусса позволяет эффективно решать системы линейных уравнений с большим количеством неизвестных. Он имеет множество приложений в физике, экономике, инженерии и других областях, где требуется решить систему уравнений для определения значений неизвестных величин.

Пример:

Рассмотрим систему линейных уравнений:

2x + y = 5

3x — 2y = 4

Применим метод Гаусса для решения данной системы:

Шаг 1: Запишем систему уравнений в матричной форме:

[2 1 | 5]

[3 -2 | 4]

Шаг 2: Приведем матрицу системы к треугольному виду:

[2 1 | 5]

[0 -2.5 | 0.5]

Шаг 3: Продолжим преобразования для получения диагональной матрицы:

[2 1 | 5]

[0 1 | -0.2]

Шаг 4: Найдем значения неизвестных:

x = 1.5

y = -0.2

Таким образом, решение данной системы линейных уравнений методом Гаусса есть x = 1.5 и y = -0.2.

Матрицы и системы уравнений

Система уравнений — это набор уравнений, которые должны быть решены одновременно. Каждое уравнение в системе имеет вид a1x1 + a2x2 + … + anxn = b, где a1, a2, …, an — коэффициенты, x1, x2, …, xn — переменные, b — свободный член.

Для решения системы уравнений можно использовать методы матричной алгебры. Для этого систему можно записать в виде матрицы. Каждое уравнение представляет собой строку матрицы, а переменные и свободные члены — элементы этой строки. Все строки объединяются в одну матрицу.

Далее, применяя различные операции строк, можно привести матрицу к ступенчатому виду или к диагональному виду, что позволяет легко решить систему уравнений.

Пример системы уравнений:

• 2x + y = 5
• 3x — 4y = 2

Матричное представление данной системы:

| 2 1 | 5 |
| 3 -4 | 2 |

Примеры использования

Приведем несколько примеров использования метода Гаусса в математике:

ПримерОписание

Пример 1	Находится сумма чисел от 1 до 100. Для этого используется формула суммы арифметической прогрессии: S = (a1 + an) * n / 2, где a1 — первый член прогрессии (в данном случае 1), an — последний член прогрессии (в данном случае 100), n — количество членов прогрессии (в данном случае 100).
Пример 2	Решается система линейных уравнений методом Гаусса. Для этого строится матрица коэффициентов и вектор свободных членов системы. Затем производится прямой ход метода Гаусса, при котором матрица приводится к ступенчатому виду. Затем производится обратный ход метода Гаусса, при котором получаются значения переменных.
Пример 3	Находится корень квадратный числа. Для этого используется формула: √a = a^(1/2). Например, чтобы найти корень квадратный числа 16, нужно возвести его в степень 1/2 и получить 4.

Это лишь некоторые примеры использования метода Гаусса. Он широко применяется в различных областях математики и физики для решения разнообразных задач.

Решение системы уравнений методом Гаусса

Для решения системы уравнений методом Гаусса необходимо выполнить следующие шаги:

1. Записать систему уравнений в виде матрицы коэффициентов.
2. Применить элементарные преобразования строк матрицы с целью привести ее к треугольному виду.
3. Решить полученную треугольную систему уравнений путем обратного хода.
4. Проверить полученное решение подстановкой в исходную систему уравнений.

Пример решения системы уравнений методом Гаусса:

Рассмотрим систему уравнений:

2x + y = 5

-x + 3y = 7

Записываем систему уравнений в виде матрицы коэффициентов:

2 1 | 5

-1 3 | 7

Применяем элементарные преобразования строк матрицы:

2 1 | 5 (Умножаем первую строку на 1/2)

0 2.5 | 8.5 (Вычитаем из второй строки первую, умноженную на -1/2)

Решаем полученную треугольную систему уравнений путем обратного хода:

2 1 | 5 (Умножаем вторую строку на 2/5)

0 1 | 3.4 (Вычитаем из первой строки вторую, умноженную на 1)

Проверяем полученное решение подстановкой в исходную систему уравнений:

2*1 + 1*3.4 = 5

-1*1 + 3*3.4 = 7

Таким образом, решение системы уравнений методом Гаусса равно:

x = 1

y = 3.4

Нахождение обратной матрицы

Чтобы найти обратную матрицу, необходимо выполнить следующие шаги:

1. Проверить, является ли исходная матрица квадратной. Обратная матрица может быть найдена только для квадратных матриц.
2. Вычислить определитель исходной матрицы. Определитель должен быть отличен от нуля. Если определитель равен нулю, то обратная матрица не существует.
3. Найти алгебраические дополнения элементов исходной матрицы. Алгебраическое дополнение элемента матрицы — это определитель матрицы, полученной путем удаления строки и столбца, в которых находится данный элемент.
4. Транспонировать матрицу алгебраических дополнений. Для этого нужно заменить элементы матрицы их соответствующими элементами из транспонированной матрицы.
5. Умножить транспонированную матрицу алгебраических дополнений на обратный определитель исходной матрицы. Полученная матрица и будет обратной матрицей.

Пример нахождения обратной матрицы:

Исходная матрица:

2	3
1	4

Определитель исходной матрицы: 2*4 — 3*1 = 5.

Алгебраические дополнения элементов исходной матрицы:

4	-3
-1	2

Транспонированная матрица алгебраических дополнений:

4	-1
-3	2

Обратная матрица:

4/5	-1/5
-3/5	2/5

Преимущества и ограничения метода Гаусса

Преимущества метода Гаусса:

1. Простота и удобство применения. Метод Гаусса является одним из основных методов решения систем линейных уравнений и широко применяется в математике и научных исследованиях.

2. Эффективность. Метод Гаусса позволяет решать системы линейных уравнений с большим количеством неизвестных и дает точные результаты.

3. Возможность применения к различным типам систем уравнений. Метод Гаусса может быть использован для решения систем уравнений с различными коэффициентами и переменными.

Ограничения метода Гаусса:

1. Требует большого объема вычислений. Метод Гаусса требует выполнения множества арифметических операций, особенно при работе с большим количеством неизвестных.

2. Метод может быть неэффективен при наличии большого количества нулевых коэффициентов. При наличии большого количества нулевых коэффициентов, метод Гаусса может потребовать большого количества шагов для решения системы уравнений.

3. Метод может быть неустойчивым при округлении. При округлении исходных данных или промежуточных результатов, метод Гаусса может давать неточные или неверные результаты.

Вопрос-ответ:

Какие основные понятия используются при применении метода Гаусса?

Основные понятия, используемые при применении метода Гаусса, включают систему линейных уравнений, матрицы, элементарные преобразования и метод прямого хода.

Какие примеры задач можно решить с помощью метода Гаусса в 5 классе математики?

С помощью метода Гаусса в 5 классе можно решать задачи на нахождение неизвестных в системе линейных уравнений, например, задачу о распределении яблок между детьми или задачу о покупке карандашей и ручек.

Как проводятся элементарные преобразования при применении метода Гаусса?

Элементарные преобразования при применении метода Гаусса включают сложение или вычитание строк, умножение строки на число и перестановку строк местами.

Какой результат дает метод Гаусса при решении системы линейных уравнений?

Метод Гаусса позволяет найти значения неизвестных в системе линейных уравнений и проверить полученное решение подстановкой в исходную систему.

Как можно применить метод Гаусса в повседневной жизни?

Метод Гаусса может быть применен в повседневной жизни, например, для решения задач по распределению ресурсов между людьми или для оптимизации процессов в производстве.

Какие понятия изучаются при изучении приема Гаусса?

При изучении приема Гаусса в 5 классе математики изучаются такие понятия, как сумма последовательности чисел, сумма первых n членов арифметической прогрессии, сумма первых n членов геометрической прогрессии.

Каким образом можно применить прием Гаусса для нахождения суммы последовательности чисел?

Для нахождения суммы последовательности чисел с помощью приема Гаусса можно использовать следующий метод: сначала определить закономерность в последовательности, а затем применить формулу для суммы n членов арифметической или геометрической прогрессии в зависимости от типа последовательности.