Что такое прием группировки в математике

Прием группировки в математике — это метод, который позволяет объединить элементы или части выражения в группы для упрощения расчетов или решения задач. В статье рассматривается основной принцип группировки и примеры его применения в различных математических задачах.

Группировка – один из основных приемов в математике, который позволяет облегчить и упростить выполнение сложных задач. Прием группировки заключается в объединении элементов или чисел в группы с целью упрощения вычислений и улучшения понимания математических операций. Он используется в различных областях математики, начиная от арифметики и алгебры, и заканчивая геометрией и математическим анализом.

Группировка может быть применена в разных контекстах. Например, при выполнении операций с многочленами, группировка позволяет объединить однотипные члены и сократить выражение до более простой формы. В арифметике группировка используется для выполнения операций с большими числами и облегчения записи вычислений. Также группировка может быть использована для выделения и анализа определенных закономерностей в последовательностях и рядах чисел.

Примером использования приема группировки может быть задача о расчете суммы чисел от 1 до 100. Вместо того, чтобы сложить все 100 чисел по отдельности, можно разбить их на группы и применить группировку. Например, можно сгруппировать числа парами (1+100), (2+99), (3+98) и так далее. В результате получится 50 пар чисел, где каждая пара будет равна 101. Таким образом, сумма всех чисел от 1 до 100 будет равна произведению количества пар (50) на значение каждой пары (101), то есть 5050.

Использование приема группировки в математике позволяет существенно упростить и расширить возможности решения задач. Он помогает наглядно представить сложные выражения и операции, а также находить закономерности и связи между числами. Прием группировки является неотъемлемой частью математического анализа и помогает развивать логическое мышление и абстрактное мышление учащихся.

Что такое прием группировки в математике?

Прием группировки в математике представляет собой метод, который позволяет объединять числа или переменные в группы для упрощения выражений и решения математических задач. Этот прием позволяет улучшить читаемость и понимание математических выражений, а также облегчить выполнение операций с числами.

Группировка может быть осуществлена с использованием скобок, квадратных или фигурных, которые помогают указать, какие элементы должны быть объединены вместе. Например, выражение (2 + 3) * 4 означает, что сначала нужно выполнить сложение чисел 2 и 3, а затем умножить результат на 4.

Прием группировки может также применяться для объединения переменных или выражений. Например, выражение 2x + 3x означает, что переменные x должны быть объединены вместе, а затем умножены на 2 и 3 соответственно. Таким образом, прием группировки позволяет упростить выражение до 5x.

Прием группировки широко используется в различных областях математики, включая алгебру, арифметику и геометрию, и является важным инструментом для работы с числами и переменными. Он помогает структурировать выражения и вычисления, делая их более понятными и удобными для работы.

Определение и основные принципы

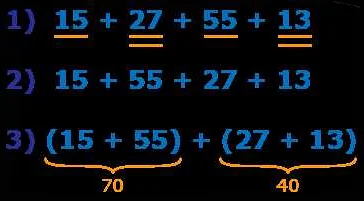
Определение и использование группировки в математике может быть полезно в различных областях, включая алгебру, геометрию и статистику. Например, группировка может быть использована для классификации чисел по их свойствам, для разделения геометрических фигур на различные классы или для анализа данных с помощью группировки значений в статистике.

Группировка может быть представлена в виде таблицы, диаграммы или списка. При этом, элементы групп могут быть упорядочены по определенному признаку, такому как числовой порядок или алфавитный порядок. Также группировка может быть иерархической, когда элементы разделены на подгруппы и подподгруппы.

Основные принципы при использовании группировки включают:

1. Выделение общих признаков у элементов.
2. Классификацию элементов в соответствии с этими признаками.
3. Упорядочение элементов в группах.
4. Изучение свойств и характеристик каждой группы.
5. Анализ и решение задач на основе группировки.

Использование приема группировки в математике позволяет упростить анализ и решение задач, а также сделать информацию более организованной и понятной.

Зачем нужен прием группировки?

Основное преимущество приема группировки заключается в том, что он позволяет изменять порядок выполнения операций и упрощать выражения. Например, при решении уравнений или систем уравнений, группировка позволяет переходить от сложных и запутанных выражений к более простым и понятным.

Кроме того, прием группировки широко используется при работе с алгебраическими выражениями, как в учебном процессе, так и в научных исследованиях. Он позволяет проводить преобразования выражений, выделять общие множители, сокращать дроби и выполнять другие операции, которые значительно упрощают алгебраические вычисления.

Также прием группировки находит применение в геометрии и аналитической геометрии, где позволяет объединять точки, отрезки, углы и другие геометрические объекты для упрощения вычислений и решения задач.

Использование приема группировки в математике позволяет значительно повысить эффективность вычислений, облегчить решение сложных задач и получить более точные и понятные результаты.

Примеры использования приема группировки

Пример 1:

Рассмотрим выражение: 3 + 4 * 2. В данном случае, умножение имеет более высокий приоритет, чем сложение. Чтобы изменить порядок операций, мы можем использовать прием группировки. При этом, результат будет зависеть от того, какие операции мы сгруппируем:

3 + (4 * 2) = 3 + 8 = 11

(3 + 4) * 2 = 7 * 2 = 14

Таким образом, прием группировки позволяет нам изменить порядок выполнения операций и получить различные результаты.

Пример 2:

Рассмотрим следующее выражение: 2 * 3 + 4 * 5. Если выполнить операции по порядку, то получим:

2 * 3 + 4 * 5 = 6 + 20 = 26

Однако, если мы применим прием группировки, можем получить другой результат:

(2 * 3) + (4 * 5) = 6 + 20 = 26

2 * (3 + 4 * 5) = 2 * (3 + 20) = 2 * 23 = 46

Таким образом, при использовании приема группировки мы можем изменить порядок операций и получить различные значения выражения.

Пример 3:

Прием группировки также может быть использован для решения уравнений. Рассмотрим следующий пример:

3 * (x + 2) = 15

Для решения данного уравнения, мы можем применить прием группировки, чтобы выделить переменную:

3x + 6 = 15

3x = 15 — 6

3x = 9

x = 3

Таким образом, прием группировки позволяет нам упростить сложные выражения, изменять порядок операций и решать уравнения.

Прием группировки в арифметике

Один из примеров использования приема группировки в арифметике – это раскрытие скобок. Когда в выражении имеются скобки, их можно раскрыть, выполнив операции внутри них, а затем объединить результаты. Например, в выражении (2 + 3) * 4, сначала выполняется операция в скобках: 2 + 3 = 5. Затем результат умножается на 4: 5 * 4 = 20.

Другой пример использования приема группировки – это сокращение выражений путем объединения подобных членов. Подобные члены – это части выражения, которые имеют одинаковые переменные и степени. Например, в выражении 3x + 2x, подобные члены 3x и 2x можно объединить, получив 5x.

Таким образом, прием группировки в арифметике помогает упростить сложные выражения, разбивая их на более простые части и затем объединяя результаты. Этот прием играет важную роль в решении различных математических задач и позволяет более эффективно выполнять арифметические операции.

Прием группировки в алгебре

Основная идея приема группировки заключается в том, чтобы объединить подобные члены в выражении, выделяя их общие множители. При этом можно использовать как общий множитель числа, так и общий множитель переменных.

Примером использования приема группировки в алгебре может быть решение квадратного уравнения. Например, при решении уравнения x^2 + 4x + 4 = 0, можно применить прием группировки следующим образом:

x^2 + 4x + 4 = (x + 2)(x + 2)

В результате применения приема группировки, выражение стало более простым и можно дальше продолжать решение уравнения.

Таким образом, прием группировки в алгебре позволяет упростить выражения и облегчить процесс решения алгебраических задач. Он является важным инструментом в алгебре и используется для решения различных математических задач.

Видео по теме:

Вопрос-ответ:

Что такое прием группировки в математике?

Прием группировки в математике — это метод, при котором элементы множества объединяются в группы на основе определенных критериев или правил.

Зачем используется прием группировки в математике?

Прием группировки в математике используется для более удобного и эффективного решения задач, упрощения вычислений и анализа данных.

Какие примеры использования приема группировки в математике?

Примерами использования приема группировки в математике могут быть суммирование ряда чисел путем их группировки, факторизация полиномов путем группировки общих множителей, классификация данных на основе заданных признаков и т.д.

Какие преимущества дает использование приема группировки в математике?

Использование приема группировки в математике позволяет упростить сложные вычисления, сократить количество шагов при решении задач, выделить общие признаки или закономерности в данных, что облегчает их анализ и понимание.

Можно ли использовать прием группировки в математике в реальной жизни?

Да, прием группировки в математике можно использовать в реальной жизни для систематизации и анализа данных, классификации объектов или явлений, оптимизации процессов и многих других задач, где требуется организация и структурирование информации.

Прием группировки в геометрии

Группировка может быть использована для классификации и идентификации объектов в геометрии. Она позволяет выделить сходство или различие между различными фигурами или элементами и упростить их анализ. Например, можно группировать треугольники по их свойствам, таким как равные стороны или углы, и исследовать их общие характеристики.

Группировка также может быть использована для решения задач геометрии. Например, при решении задачи на построение геометрической фигуры, можно использовать группировку для объединения нескольких элементов в одну группу и работать с ними как с одним объектом. Это может значительно упростить процесс решения и помочь достичь желаемого результата.

В геометрии группировка может быть полезным инструментом для визуализации и понимания различных геометрических концепций. Она позволяет увидеть связь и взаимодействие между элементами и фигурами, что помогает лучше понять и запомнить геометрические правила и свойства.

В заключение, прием группировки является полезным инструментом в геометрии, который помогает упростить решение задач и анализ геометрических объектов. Он позволяет классифицировать и идентифицировать объекты, решать задачи и визуализировать геометрические концепции. Использование этого приема может значительно улучшить понимание и применение геометрии.

Выводы

В данной статье мы рассмотрели понятие приема группировки в математике и его применение. Группировка позволяет облегчить сложные математические выражения, объединяя их в более компактную и удобную форму. Этот прием особенно полезен при работе с алгебраическими выражениями, рациональными функциями, уравнениями и прочими математическими объектами.

Мы изучили основные правила группировки, такие как использование скобок, приоритет операций, ассоциативность и коммутативность. Также были рассмотрены конкретные примеры применения группировки, например, при факторизации полиномов, решении уравнений и вычислении арифметических выражений.

Прием группировки является мощным инструментом в математике, который помогает упростить сложные задачи и улучшить понимание математических концепций. Он позволяет не только сократить количество операций, но и легче анализировать и решать сложные математические проблемы.

Важно понимать, что группировка не является единственным приемом в математике, и ее использование требует навыков и понимания основных математических концепций. Однако, при правильном применении, группировка помогает сделать математические вычисления более легкими и эффективными.

В заключение, прием группировки является важным инструментом в математике, который помогает упростить сложные математические выражения и улучшить понимание математических концепций. Он может применяться в самых разных областях математики и широко используется при решении задач алгебры, арифметики, геометрии и других математических дисциплин.