Что такое прогрессия в математике

Прогрессия в математике — это последовательность чисел или терминов, которая развивается по определенному закону. В статье рассказывается о различных типах прогрессий, их свойствах и применении в решении задач и формулах.

Прогрессия — это последовательность чисел, в которой каждый следующий элемент получается путем определенного правила или закона. Она является одной из основных тем в математике и имеет важное значение в различных областях науки, экономики и физики.

Типы прогрессий включают арифметическую прогрессию, геометрическую прогрессию и гармоническую прогрессию. В арифметической прогрессии каждый следующий элемент получается путем прибавления одного и того же фиксированного числа к предыдущему элементу. В геометрической прогрессии каждый следующий элемент получается путем умножения предыдущего элемента на фиксированный множитель. В гармонической прогрессии каждый следующий элемент получается путем деления фиксированного числа на предыдущий элемент.

Примеры прогрессий помогают лучше понять их суть. Например, арифметическая прогрессия может быть представлена последовательностью чисел 2, 5, 8, 11, 14, где каждый следующий элемент получается путем прибавления 3 к предыдущему элементу. Геометрическая прогрессия может быть представлена последовательностью чисел 3, 6, 12, 24, 48, где каждый следующий элемент получается путем умножения предыдущего элемента на 2. Гармоническая прогрессия может быть представлена последовательностью чисел 1/2, 1/3, 1/4, 1/5, 1/6, где каждый следующий элемент получается путем деления 1 на предыдущий элемент.

Прогрессия — это неотъемлемая часть математики, которая используется для решения широкого спектра задач. Понимание различных типов и примеров прогрессий позволяет лучше анализировать и решать сложные математические проблемы, а также применять их в реальной жизни.

Что такое прогрессия в математике?

Прогрессия может быть арифметической или геометрической. В арифметической прогрессии каждое следующее число получается путем добавления к предыдущему числу одного и того же числа, называемого разностью. Например: 1, 3, 5, 7, 9 — это арифметическая прогрессия с разностью 2.

В геометрической прогрессии каждое следующее число получается путем умножения предыдущего числа на одно и то же число, называемое знаменателем. Например: 2, 4, 8, 16, 32 — это геометрическая прогрессия с знаменателем 2.

Прогрессии являются важным инструментом для анализа и решения различных задач в математике и других науках. Они позволяют нам прогнозировать и предсказывать изменения величин и явления, а также находить законы и закономерности в реальном мире.

Арифметическая прогрессия: определение и свойства

Основные свойства арифметической прогрессии:

• Разность прогрессии (d) — это постоянное число, на которое увеличивается (или уменьшается) каждый член последовательности.
• Первый член прогрессии (a1) — это начальное число в последовательности.
• Общий член прогрессии (an) — это n-е число в последовательности.
• Формула для общего члена прогрессии: an = a1 + (n — 1) * d.
• Количество членов прогрессии (n) — это порядковый номер последнего числа в последовательности.
• Сумма n членов прогрессии (Sn) — это сумма всех чисел от первого до n-го члена прогрессии.
• Формула для суммы n членов прогрессии: Sn = (n / 2) * (2 * a1 + (n — 1) * d).

Арифметическая прогрессия широко используется в математике и других науках для моделирования и анализа различных явлений и процессов.

Геометрическая прогрессия: определение и особенности

Особенностью геометрической прогрессии является то, что отношение любых двух последовательных элементов будет постоянным числом, знаменателем прогрессии. Если знаменатель положителен, то прогрессия будет возрастающей, а если знаменатель отрицателен, то прогрессия будет убывающей.

Каждый элемент геометрической прогрессии можно найти по формуле:

an = a1 * r(n-1)

где an — n-й элемент прогрессии, a1 — первый элемент прогрессии, r — знаменатель прогрессии, n — номер элемента.

Пример геометрической прогрессии: 1, 2, 4, 8, 16. В данном примере первый элемент равен 1, а знаменатель равен 2. Каждый следующий элемент получается путем умножения предыдущего элемента на 2.

Формула общего члена арифметической прогрессии

В арифметической прогрессии каждый следующий член ряда получается путем прибавления к предыдущему члену одного и того же числа, которое называется разностью арифметической прогрессии.

Общий член арифметической прогрессии можно найти с помощью формулы:

an = a1 + (n — 1)d,

где an — общий член прогрессии,

a1 — первый член прогрессии,

n — номер члена прогрессии,

d — разность арифметической прогрессии.

Например, рассмотрим арифметическую прогрессию с первым членом a1 = 2 и разностью d = 3. Чтобы найти 5-й член прогрессии, подставим значения в формулу:

a5 = 2 + (5 — 1) * 3 = 2 + 4 * 3 = 2 + 12 = 14.

Таким образом, 5-й член арифметической прогрессии равен 14.

Формула общего члена геометрической прогрессии

Формула общего члена геометрической прогрессии имеет вид:

an = a1 * r(n-1)

где:

• an — значение n-го члена геометрической прогрессии;
• a1 — значение первого члена геометрической прогрессии;
• r — знаменатель прогрессии;
• n — номер члена геометрической прогрессии, для которого мы хотим найти значение.

Эта формула позволяет находить любой член геометрической прогрессии, если известны первый член и знаменатель прогрессии.

Пример:

Рассмотрим геометрическую прогрессию, в которой первый член равен 2, а знаменатель прогрессии равен 3. Найдем значение 5-го члена прогрессии, используя формулу общего члена:

a5 = 2 * 3(5-1) = 2 * 34 = 2 * 81 = 162

Таким образом, пятый член геометрической прогрессии с первым членом 2 и знаменателем 3 равен 162.

Видео по теме:

Вопрос-ответ:

Что такое прогрессия в математике?

Прогрессия в математике — это последовательность чисел, где каждое следующее число получается путем определенной операции или правила преобразования предыдущего числа.

Какие типы прогрессий существуют?

Существуют разные типы прогрессий в математике, включая арифметическую прогрессию, геометрическую прогрессию, гармоническую прогрессию и фибоначчиеву прогрессию.

Что такое арифметическая прогрессия?

Арифметическая прогрессия — это последовательность чисел, где каждое следующее число получается путем добавления к предыдущему числу постоянного числа, называемого разностью.

Можете привести пример арифметической прогрессии?

Конечно! Примером арифметической прогрессии может быть последовательность чисел 2, 5, 8, 11, 14, 17, где разность между каждыми двумя соседними числами равна 3.

Рекуррентная формула и различные типы прогрессий

Существует несколько различных типов прогрессий, каждый из которых имеет свою рекуррентную формулу.

Арифметическая прогрессия – это прогрессия, в которой каждый следующий член получается путем прибавления к предыдущему члену постоянного числа, называемого разностью. Рекуррентная формула для арифметической прогрессии имеет вид:

an = an-1 + d

где an – n-й член прогрессии, an-1 – предыдущий член прогрессии, d – разность.

Геометрическая прогрессия – это прогрессия, в которой каждый следующий член получается путем умножения предыдущего члена на постоянное число, называемое знаменателем. Рекуррентная формула для геометрической прогрессии имеет вид:

an = an-1 * q

где an – n-й член прогрессии, an-1 – предыдущий член прогрессии, q – знаменатель.

Арифметико-геометрическая прогрессия – это прогрессия, в которой каждый следующий член получается как сумма арифметической и геометрической прогрессий. Рекуррентная формула для арифметико-геометрической прогрессии имеет вид:

an = an-1 + d + an-1 * q

где an – n-й член прогрессии, an-1 – предыдущий член прогрессии, d – разность арифметической прогрессии, q – знаменатель геометрической прогрессии.

Использование рекуррентных формул позволяет удобно и эффективно находить любой член прогрессии, зная только начальный член и параметры прогрессии.

Примеры прогрессий в реальной жизни

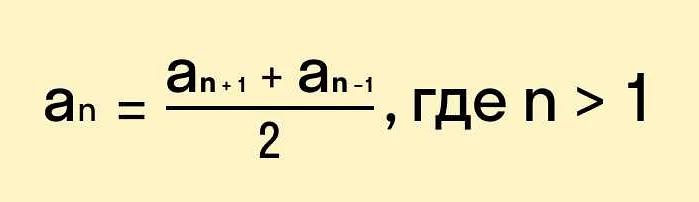
1. Арифметическая прогрессия:
   • Увеличение ежегодного дохода на постоянную сумму.
   • Рост численности населения города каждый год на одинаковое количество человек.
   • Увеличение скорости автомобиля на постоянное значение каждую секунду.
2. Геометрическая прогрессия:
   • Увеличение суммы вклада на постоянный процент каждый год.
   • Увеличение стоимости товара на постоянное значение каждый месяц.
   • Рост популяции бактерий с постоянным коэффициентом размножения.
3. Фибоначчиева последовательность:
   • Рост числа лепестков на цветке.
   • Распределение листьев по ветвям растения.
   • Размещение семян в цветке.

Это лишь некоторые примеры прогрессий, которые можно встретить в реальной жизни. Они помогают нам понять и описать различные процессы и явления, а также использовать эти знания в нашей повседневной жизни.