Что такое простые числа 5 класс в математике

Простые числа в математике – это числа, которые имеют только два делителя: единицу и само число. В этой статье рассмотрим, что такое простые числа в 5 классе и как их определить. Узнайте, какие числа являются простыми, и какие алгоритмы можно использовать для их поиска.

Простые числа — это числа, которые имеют только два делителя: 1 и само число. Они не делятся ни на какие другие числа. Простые числа являются основой для многих математических концепций и имеют важное значение в криптографии и теории чисел.

В пятом классе математики учатся определять и работать с простыми числами. Для этого нужно знать, как проверить, является ли число простым, и как найти все простые числа до определенного числа.

Чтобы проверить, является ли число простым, достаточно просто проверить, делится ли оно на какое-либо число, кроме 1 и самого себя. Если число делится на другое число без остатка, оно не является простым. Если же число не делится ни на одно другое число, кроме 1 и самого себя, то оно простое.

Например, число 7 является простым, потому что оно не делится ни на какое другое число, кроме 1 и 7. Однако число 8 не является простым, потому что оно делится на 2 и 4.

Что такое простые числа?

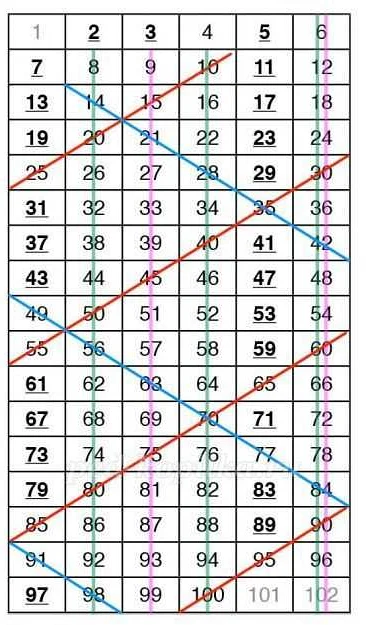
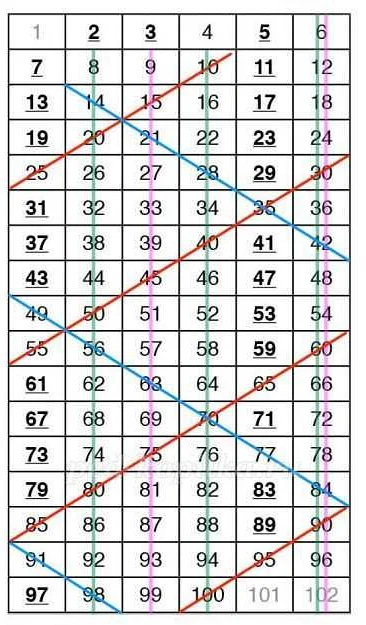
Простые числа являются основой для многих алгоритмов и математических задач. Они используются в криптографии, теории чисел, а также в науке и технологии. Например, простые числа используются в алгоритме RSA для шифрования данных.

Знание простых чисел и их свойств помогает понять многие аспекты математики и решать различные задачи. Выделение простых чисел из общего ряда чисел позволяет упростить анализ и решение задач, а также найти особые закономерности и связи между числами.

Составные числа и их отличие от простых чисел

Составные числа — это числа, которые имеют больше двух делителей. Другими словами, они делятся не только на 1 и на само число, но и на другие числа. Например, число 4 — составное, потому что оно делится не только на 1 и на 4, но и на 2. А число 9 — тоже составное, потому что оно делится на 1, 3 и 9.

Отличие составных чисел от простых заключается в количестве их делителей. У простых чисел только два делителя, а у составных чисел их может быть больше двух. Также, простые числа не могут быть разложены на множители, а составные числа могут быть представлены как произведение простых чисел.

Например, число 12 — составное, потому что оно делится на 1, 2, 3, 4, 6 и 12. Также, число 12 можно разложить на множители: 12 = 2 * 2 * 3.

Изучение составных чисел помогает нам лучше понять структуру чисел и их свойства. Это также помогает в решении различных задач и проблем в математике и других науках.

Как определить, является ли число простым?

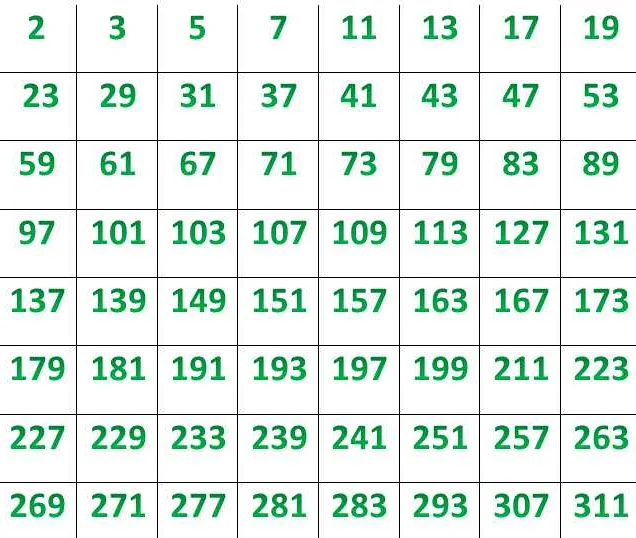
Давайте рассмотрим пример. Проверим, является ли число 17 простым. Для этого нужно проверить, делится ли оно без остатка на числа, начиная от 2 и заканчивая корнем из этого числа. В нашем случае, число 17 делится без остатка только на себя и на 1, значит, оно является простым числом.

Определение простого числа может быть полезным при решении различных задач. Например, оно может помочь нам найти все простые числа в заданном диапазоне или разложить число на простые множители.

Теперь вы знаете, как определить, является ли число простым. Помните, что простые числа – это особый класс чисел, и они имеют важные свойства и приложения в математике.

Примеры простых чисел

Пример 1: Число 2 является простым числом, так как его единственные делители — 1 и 2.

Пример 2: Число 3 также является простым числом, так как его единственные делители — 1 и 3.

Пример 3: Число 5 — еще одно простое число, так как его единственные делители — 1 и 5.

Пример 4: Число 7 также является простым числом, поскольку его единственные делители — 1 и 7.

Это лишь некоторые примеры простых чисел. Они являются основой для более сложных математических понятий и алгоритмов.

Знание простых чисел помогает в решении задач, связанных с делимостью и разложением чисел на множители. Они имеют важное значение в различных областях науки и техники.

Неопределенность в разложении числа на простые множители может быть устранена с помощью теоремы Фундаментальной арифметики, которая утверждает, что каждое натуральное число может быть представлено в виде произведения простых чисел, причем это представление единственное с точностью до порядка сомножителей.

Как найти все простые числа до заданного числа?

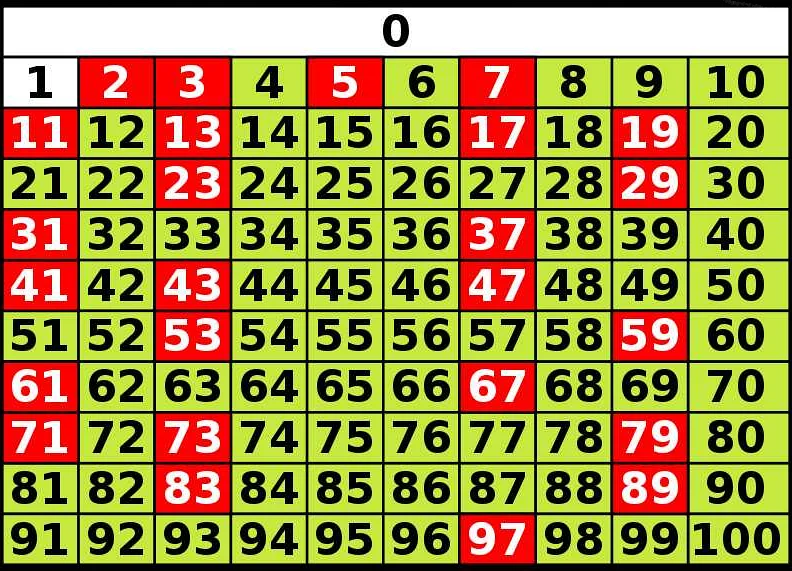
Существует несколько методов для поиска всех простых чисел до заданного числа, но один из наиболее эффективных методов — это метод Решета Эратосфена.

Метод Решета Эратосфена основан на следующих шагах:

1. Создайте список всех чисел от 2 до заданного числа.
2. Начните с первого числа в списке и пометьте его как простое.
3. Удалите все числа в списке, которые делятся на это простое число (кроме самого числа).
4. Перейдите к следующему числу в списке и повторите шаги 2 и 3.
5. Повторяйте шаги 2-4, пока не достигнете конца списка.
6. Оставшиеся числа в списке будут простыми числами.

Например, попробуем найти все простые числа до числа 20:

Создаем список чисел от 2 до 20: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20.

Начинаем с первого числа — 2. Помечаем его как простое и удаляем все числа в списке, которые делятся на 2 (кроме самого числа 2): 3, 5, 7, 9, 11, 13, 15, 17, 19.

Переходим к следующему числу — 3. Помечаем его как простое и удаляем все числа в списке, которые делятся на 3 (кроме самого числа 3): 5, 7, 11, 13, 17, 19.

Продолжаем этот процесс для всех оставшихся чисел в списке и получаем следующий список простых чисел до числа 20: 2, 3, 5, 7, 11, 13, 17, 19.

Таким образом, все простые числа до числа 20 равны 2, 3, 5, 7, 11, 13, 17, 19.

Факторизация числа на простые множители

Для факторизации числа на простые множители необходимо последовательно делить это число на простые числа, начиная с наименьшего. Если число делится на простое число без остатка, то оно является множителем данного числа. Если число не делится на простое число без остатка, то нужно перейти к следующему простому числу и повторить процесс.

Процесс факторизации можно продолжать до тех пор, пока не останется простое число, которое делит исходное число без остатка. В результате получается разложение числа на простые множители, которые перемножаются между собой и дают исходное число.

Например, рассмотрим число 24:

24 = 2 × 12

12 = 2 × 6

6 = 2 × 3

Итак, факторизация числа 24 на простые множители будет: 2 × 2 × 2 × 3 = 2^3 × 3

Факторизация числа на простые множители помогает нам решать различные задачи, связанные с числами, такие как нахождение наибольшего общего делителя, нахождение наименьшего общего кратного и решение уравнений и неравенств.

Видео по теме:

Вопрос-ответ:

Что такое простые числа?

Простые числа — это натуральные числа, которые имеют только два делителя: 1 и само число. Они не делятся на другие числа без остатка.

Как определить, является ли число простым?

Чтобы определить, является ли число простым, нужно проверить, делится ли оно на любое число от 2 до корня из этого числа без остатка. Если делится, то число составное, если нет — простое.

Приведите примеры простых чисел.

Примеры простых чисел: 2, 3, 5, 7, 11, 13, 17, 19 и так далее.

Зачем нужно знать простые числа в математике?

Знание простых чисел в математике имеет важное значение. Они используются в различных областях, таких как шифрование данных, теория чисел, факторизация и других математических алгоритмах.

Свойства простых чисел

1. Бесконечность простых чисел: Математики установили, что простых чисел бесконечное множество. Это означает, что всегда можно найти новое простое число, большее заданного числа.

2. Уникальность разложения: Каждое натуральное число больше единицы может быть представлено в виде произведения простых чисел. Это разложение является уникальным, то есть не зависит от порядка простых множителей.

3. Основная теорема арифметики: Она утверждает, что каждое натуральное число больше единицы может быть представлено в виде произведения простых чисел только одним способом (с точностью до порядка множителей).

4. Неразложимость на меньшие множители: Простые числа не могут быть разложены на меньшие простые множители. Это означает, что простое число не делится на другое простое число.

5. Относительная плотность: Простые числа распределены в наборе натуральных чисел сравнительно равномерно. Из этого следует, что простых чисел бесконечно много, но их плотность уменьшается по мере увеличения числа.

Практическое применение простых чисел

ПрименениеОписание

Шифрование данных	Простые числа играют важную роль в криптографии, особенно в асимметричном шифровании. Они используются для генерации ключей и защиты данных от несанкционированного доступа.
Создание кодов	Простые числа используются для создания уникальных кодов, например, в системах идентификации, баркодах или QR-кодах. Такие коды обеспечивают уникальность и надежность информации.
Тестирование на простоту	Простые числа используются для проверки других чисел на простоту. Это важный инструмент в математике и криптографии для определения простоты чисел и построения эффективных алгоритмов.

Простые числа имеют еще много других применений в различных областях, таких как теория чисел, алгоритмы и даже в музыке. Изучение простых чисел помогает развивать логическое мышление, аналитические навыки и способность решать сложные задачи.