Рациональные уравнения как математические модели реальных ситуаций 8 класс

Рациональные уравнения — это математические модели, которые позволяют описывать реальные ситуации в учебной программе по математике для 8 класса. В данной статье рассмотрены основные принципы построения и решения рациональных уравнений, а также их применение в решении задач различной сложности. Узнайте, как использовать рациональные уравнения для моделирования реальных ситуаций и справиться с заданиями по математике в 8 классе.

Рациональные уравнения — это уравнения, в которых содержатся одно или несколько рациональных выражений. В математике 8 класса ученики изучают и анализируют различные типы рациональных уравнений и осваивают методы их решения.

Одной из важных областей применения рациональных уравнений является моделирование реальных ситуаций. Моделирование позволяет связать математические концепции с реальными проблемами и создать абстрактные модели для их решения. В 8 классе ученики изучают основные принципы моделирования и применяют их для анализа и решения рациональных уравнений.

Примером моделирования реальной ситуации с использованием рациональных уравнений может быть задача о смешивании различных растворов. Ученикам предлагается решить уравнение, чтобы определить, какое количество различных составляющих необходимо смешать, чтобы получить определенную концентрацию раствора. Эта задача требует применения знаний о пропорциях и рациональных выражениях.

Таким образом, изучение рациональных уравнений и их применение для моделирования реальных ситуаций способствует развитию математического мышления, логического рассуждения и практических навыков учащихся. В результате такого обучения ученики смогут применять свои знания в реальных жизненных ситуациях и принимать обоснованные решения.

Основные определения и понятия

Одним из ключевых понятий в рациональных уравнениях является понятие домена. Доменом уравнения называется множество значений переменной, для которых уравнение является выполнимым. Например, в уравнении 1/x = 2 доменом будет множество всех значений переменной x, за исключением значения x = 0, так как деление на ноль невозможно.

Другим важным понятием является решение рационального уравнения. Решением уравнения называется такое значение переменной, которое делает его истинным. Например, в уравнении 1/x = 2 решением будет значение переменной x = 1/2, так как при подстановке этого значения уравнение становится верным: 1/(1/2) = 2.

При решении рациональных уравнений могут возникать также случаи, когда уравнение не имеет решений или имеет бесконечное количество решений. Например, уравнение 1/x = 0 не имеет решений, так как не существует такого числа, которое умноженное на ноль давало бы единицу.

Для решения рациональных уравнений часто используют методы сокращения дробей, приведение к общему знаменателю, а также применение свойств алгебры. При решении задач, моделирующих реальные ситуации с помощью рациональных уравнений, необходимо также проводить проверку полученных решений на соответствие условиям задачи.

ПонятиеОписание

Рациональное уравнение	Уравнение, в котором искомой переменной является рациональное число.
Домен	Множество значений переменной, для которых уравнение является выполнимым.
Решение	Значение переменной, которое делает уравнение истинным.

Методы решения рациональных уравнений

Существует несколько методов решения рациональных уравнений:

МетодОписание

Умножение на общий знаменатель	Умножение уравнения на общий знаменатель всех дробей в уравнении, чтобы избавиться от дробей.
Применение формулы сложения дробей	Применение формулы сложения дробей для объединения дробей с общим знаменателем в одну дробь.
Факторизация	Факторизация уравнения для упрощения выражений и поиска общих множителей.
Замена переменной	Замена переменной для создания нового уравнения, которое может быть решено более простым способом.

При решении рациональных уравнений необходимо также проверять полученные корни на допустимость, исключая значения переменных, при которых знаменатель становится равным нулю.

Примеры моделирования реальных ситуаций с помощью рациональных уравнений

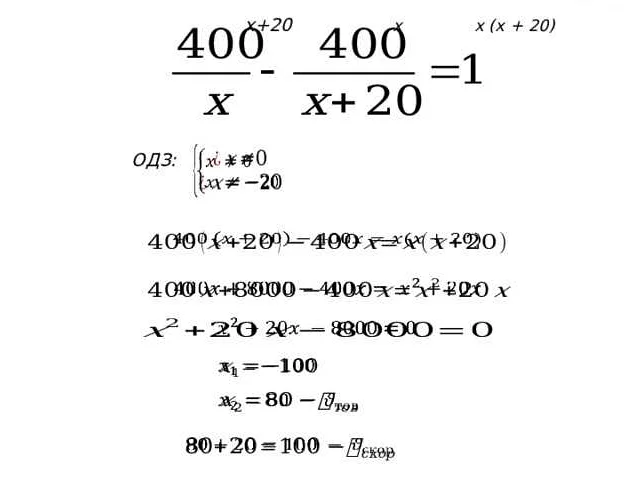
Пример 1: Скорость движения

Предположим, что автомобиль движется по прямой дороге со скоростью v км/ч. Мы можем использовать рациональное уравнение для определения времени, которое автомобиль затратит на прохождение определенного расстояния. Уравнение может иметь вид:

t = d/v

где t — время (в часах), d — расстояние (в километрах) и v — скорость (в километрах в час). Это уравнение позволяет нам моделировать время, которое требуется автомобилю для достижения определенной точки на дороге в зависимости от его скорости.

Пример 2: Поток вещества

Представим, что вода вытекает из открытого резервуара через отверстие. Мы можем использовать рациональное уравнение для моделирования скорости потока в зависимости от диаметра отверстия и высоты уровня воды в резервуаре. Уравнение может иметь вид:

v = k√h/d

где v — скорость потока (в литрах в секунду), k — постоянная, зависящая от физических свойств вещества, h — высота уровня воды (в метрах) и d — диаметр отверстия (в метрах). Это уравнение позволяет нам моделировать скорость потока воды из резервуара в зависимости от изменения высоты уровня и диаметра отверстия.

Пример 3: Изменение температуры

Предположим, что температура в помещении меняется со временем. Мы можем использовать рациональное уравнение для моделирования изменения температуры в зависимости от времени. Уравнение может иметь вид:

T = a/(b + ct)

где T — температура (в градусах Цельсия), a, b и c — коэффициенты, зависящие от физических свойств системы, а t — время (в минутах). Это уравнение позволяет нам моделировать изменение температуры в помещении в зависимости от прошедшего времени.

Это лишь несколько примеров того, как рациональные уравнения можно использовать для моделирования реальных ситуаций. Они помогают нам лучше понять и анализировать различные явления в нашей окружающей среде и прогнозировать их поведение.

Значение рациональных уравнений в реальной жизни

Рациональные уравнения широко применяются в физике, экономике, биологии и других науках для описания различных явлений и процессов.

Например, в экономике рациональные уравнения могут использоваться для определения равновесной цены товара или объема производства. Они позволяют моделировать зависимости между спросом, предложением и ценой, а также прогнозировать изменения в этих величинах.

В физике рациональные уравнения часто применяются для описания движения тела, изменения его скорости или ускорения. Они позволяют решать задачи о движении тела под действием силы тяжести, сопротивления среды и других факторов.

Рациональные уравнения также находят применение в биологии для описания процессов роста, развития и распределения популяций. Они позволяют моделировать изменения численности организмов в зависимости от различных факторов, таких как доступность пищи, наличие хищников и условия среды.

Таким образом, знание рациональных уравнений позволяет анализировать и предсказывать различные процессы и явления, встречающиеся в реальной жизни. Они помогают нам понять и объяснить мир вокруг нас, а также принимать более обоснованные решения в различных областях деятельности.

Видео по теме:

Вопрос-ответ:

Что такое рациональные уравнения?

Рациональные уравнения — это уравнения, в которых неизвестное присутствует в знаменателе дроби. Они могут быть представлены в виде отношения двух многочленов.

Какие примеры реальных ситуаций можно моделировать с помощью рациональных уравнений?

Например, можно использовать рациональные уравнения для моделирования задач, связанных с расчетом скорости течения реки, расходом топлива автомобиля, изменением уровня жидкости в сосуде и других подобных ситуаций.

Как решать рациональные уравнения?

Для решения рациональных уравнений нужно привести уравнение к общему знаменателю и решить полученное уравнение без знаменателей. Затем проверить полученные значения и отбросить те, которые приводят к недопустимым значениям в знаменателе.

Каковы основные шаги при моделировании реальной ситуации с помощью рациональных уравнений?

Основные шаги при моделировании реальной ситуации с помощью рациональных уравнений: сформулировать задачу, выразить неизвестное значение в виде переменной, составить уравнение, решить его и проанализировать полученное решение с точки зрения задачи.

Каковы особенности решения рациональных уравнений?

Особенностью решения рациональных уравнений является необходимость проверки полученных корней уравнения, так как некоторые из них могут приводить к недопустимым значениям в знаменателе. Также важно учитывать, что решениями могут быть не только числа, но и выражения.

Какие рациональные уравнения встречаются в реальных ситуациях?

В реальных ситуациях могут возникать различные рациональные уравнения, например, уравнения, описывающие скорость движения объекта, объемы смесей, временные интервалы и т. д.

Использование программного обеспечения для решения рациональных уравнений

Программное обеспечение для решения рациональных уравнений предоставляет возможность использования компьютерных алгоритмов для автоматического нахождения корней уравнений. Такое ПО позволяет экономить время и усилия, особенно при работе с сложными уравнениями или системами уравнений.

Одним из популярных программных инструментов для решения рациональных уравнений является математический пакет Maple. Maple обладает широким набором функций, позволяющих не только решить уравнение, но и построить графики функций, найти аналитические производные, интегралы и многое другое.

Для решения рационального уравнения в Maple необходимо ввести уравнение в символьном виде, используя соответствующие операторы и функции. Maple выполнит вычисления и выведет все возможные значения переменных, при которых уравнение имеет решение. При этом, Maple также может предоставить графическое представление решения в виде графика или таблицы значений.

Другим популярным программным инструментом для решения рациональных уравнений является математический пакет Mathematica. Mathematica также предлагает широкий спектр функций и возможностей для работы с математическими объектами.

В Mathematica, рациональные уравнения могут быть решены с помощью встроенной функции, принимающей уравнение в символьном виде и возвращающей все значения переменных, при которых уравнение имеет решение. Также в Mathematica можно построить графики решений и выполнить другие математические операции.

При использовании программного обеспечения для решения рациональных уравнений, необходимо иметь хорошее понимание математических концепций и умение формулировать уравнения правильно. Также важно уметь интерпретировать результаты, полученные с помощью программного обеспечения.

Программное обеспечениеОсобенности

Maple	Широкий набор функций, графическое представление решений
Mathematica	Встроенные функции, графическое представление решений

Использование программного обеспечения для решения рациональных уравнений делает процесс нахождения решений более эффективным и точным. Это позволяет математикам, инженерам и другим специалистам решать сложные уравнения и моделировать реальные ситуации с большей точностью и уверенностью.

Практические задания и упражнения для закрепления материала

Для закрепления материала по рациональным уравнениям в 8 классе, предлагаем следующие практические задания:

1. Решите уравнение 2/(x+3) + 1/(x-2) = 3/(2x).
2. Найдите все значения переменной x, для которых уравнение (x-1)/(2x+3) — 2/(x+5) = 1/(x-2) имеет смысл.
3. Решите уравнение (3x+2)/(x-1) + (2x-3)/(3x+1) = 1.
4. Найдите все значения переменной x, при которых уравнение (x+1)/(2x) — (x-2)/(x+3) = 1/3 существует.

Для каждого уравнения, необходимо предоставить подробное решение, объясняя каждый шаг. Также, рекомендуется проверить полученные значения переменной x в исходном уравнении, чтобы убедиться в их правильности.

Данные задания помогут закрепить навыки решения рациональных уравнений аналитическими методами и применить их на практике. Успехов в выполнении!