На чем основаны методы математического моделирования
Содержимое
- 1 На чем основаны методы математического моделирования
- 1.1 Основные принципы математического моделирования
- 1.2 Изучение объекта моделирования
- 1.3 Выбор математической модели
- 1.4 Построение математической модели
- 1.5 Оценка и анализ результатов моделирования
- 1.6 Применение математического моделирования в различных областях
- 1.7 Математическое моделирование в экономике
- 1.8 Математическое моделирование в физике
- 1.9 Математическое моделирование в биологии
- 1.10 Вопрос-ответ:
- 1.10.0.1 Какие методы математического моделирования существуют?
- 1.10.0.2 Какие принципы лежат в основе математического моделирования?
- 1.10.0.3 В каких областях применяются методы математического моделирования?
- 1.10.0.4 Какую роль играет математическое моделирование в научных исследованиях?
- 1.10.0.5 Какие методы математического моделирования существуют?
- 1.10.0.6 Какие принципы лежат в основе математического моделирования?
- 1.11 Видео по теме:
В статье рассматриваются основные принципы и методы математического моделирования, включая математические модели, статистические методы, дифференциальные уравнения и теорию вероятностей. Описывается роль математического моделирования в науке и практических приложениях, а также примеры его использования в различных областях знания.
Математическое моделирование – это процесс создания математических моделей, которые позволяют описывать и анализировать различные явления и системы. Основная идея заключается в том, что сложные реальные объекты и процессы могут быть представлены в виде упрощенных математических моделей, которые позволяют проводить различные исследования и прогнозы.
Основными принципами математического моделирования являются абстракция, формализация и верификация. Абстракция предполагает упрощение исследуемого объекта или процесса, выделение только главных характеристик и игнорирование незначительных деталей. Формализация заключается в описании объекта или процесса с помощью математических символов, уравнений и операций. Верификация представляет собой проверку математической модели на соответствие реальным наблюдениям и экспериментальным данным.
Математическое моделирование применяется во многих областях науки и техники. Оно используется для изучения физических процессов в различных отраслях промышленности, аэродинамике, экологии, биологии и многих других. Моделирование позволяет предсказывать поведение системы в различных условиях, оптимизировать ее параметры, а также планировать эксперименты и проводить виртуальные тесты.
Одним из примеров успешного применения математического моделирования является прогнозирование погоды с помощью численных моделей атмосферы. Такие модели позволяют рассчитывать изменение температуры, давления, скорости ветра и других параметров в различных точках земной поверхности. Это позволяет прогнозировать погоду на несколько дней вперед, что является важным инструментом для сельского хозяйства, туризма, авиации и других отраслей.
Таким образом, математическое моделирование играет важную роль в современной науке и технике, позволяя проводить исследования, делать прогнозы и принимать обоснованные решения. Оно объединяет математику, физику, информатику и другие научные дисциплины, предоставляя универсальный инструмент для изучения сложных систем и процессов.
Основные принципы математического моделирования
Основные принципы математического моделирования включают:
- Идентификация проблемы: определение системы или явления, которые требуют моделирования. Это может быть физический объект, процесс, социальная система и т.д.
- Выбор подхода: выбор математических методов и моделей, которые наилучшим образом описывают систему или явление. Это может быть дифференциальные уравнения, стохастические модели, оптимизационные задачи и т.д.
- Сбор данных: сбор и анализ данных, необходимых для построения и валидации модели. Это может включать эксперименты, наблюдения, исторические данные и т.д.
- Разработка модели: создание математической модели, которая описывает систему или явление. Модель должна быть адекватной, точной и удобной для анализа.
- Проверка и валидация: проверка модели на соответствие реальным данным и проверка ее способности предсказывать поведение системы.
- Использование модели: использование модели для анализа и оптимизации системы, прогнозирования будущих событий и принятия решений.
Математическое моделирование имеет широкое применение в различных областях, таких как физика, экономика, биология, климатология и др. Оно позволяет исследовать сложные системы, которые не могут быть полностью изучены экспериментально или аналитически. Математическое моделирование способствует развитию науки и технологий, а также принятию важных решений в различных областях деятельности.
Изучение объекта моделирования
Для проведения исследования объекта моделирования могут использоваться различные методы, включая наблюдение, эксперименты, анализ данных и теоретические рассуждения. Важно собрать достаточно информации для построения адекватной математической модели, которая бы точно отражала поведение объекта в реальном мире.
В процессе изучения объекта моделирования часто требуется собрать и систематизировать данные, относящиеся к его характеристикам. Это может включать информацию о размерах, форме, структуре, функциях и взаимодействиях с другими объектами. Для удобства организации данных часто используется таблица.
ХарактеристикаОписание
| Размеры | Определенные значения, характеризующие размеры объекта |
| Форма | Особенности формы объекта, например, геометрические параметры |
| Структура | Организация внутренних компонентов объекта |
| Функции | Основные функции, выполняемые объектом |
| Взаимодействия | Способы взаимодействия с окружающими объектами или средой |
После того, как все необходимые данные были собраны и систематизированы, можно приступить к построению математической модели. Она должна учитывать все изученные характеристики объекта и взаимосвязи между ними.
Изучение объекта моделирования является важным этапом в разработке математической модели, поскольку от корректности и полноты собранных данных зависит точность и достоверность модели, а значит и ее применимость для решения практических задач.
Выбор математической модели
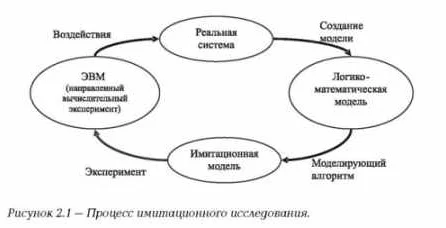
При разработке математической модели необходимо учесть множество факторов, чтобы получить реалистичное и точное описание системы или процесса. Выбор математической модели зависит от целей и требований исследования, а также доступных данных и ресурсов.
Важным этапом выбора модели является анализ предметной области. Необходимо определить, какие переменные и параметры являются ключевыми и как они взаимодействуют между собой. Также необходимо определить, какие законы и правила описывают систему или процесс, и какие предположения могут быть сделаны.
После анализа предметной области можно приступить к выбору конкретной математической модели. Существует множество типов моделей, таких как дифференциальные уравнения, стохастические модели, вероятностные модели и другие. Каждый тип модели имеет свои преимущества и ограничения, поэтому необходимо выбирать модель, наиболее подходящую для конкретной задачи.
Кроме того, при выборе модели необходимо учитывать доступные данные и ресурсы. Некоторые модели требуют большого количества данных для обучения и повышения точности, в то время как другие модели могут быть более простыми и требовать меньше ресурсов.
Важно помнить, что математическая модель является упрощенным описанием реальной системы или процесса. Поэтому необходимо проводить проверку и анализ полученных результатов моделирования, сравнивая их с реальными данными и наблюдениями.
В заключение, выбор математической модели является сложным процессом, требующим внимательного анализа и оценки. Необходимо учитывать цели и требования исследования, доступные данные и ресурсы, а также проводить проверку полученных результатов. Только таким образом можно создать модель, которая будет наиболее точно описывать и анализировать изучаемую систему или процесс.
Построение математической модели

Основная задача при построении математической модели заключается в преобразовании сложных реальных объектов или процессов в абстрактные математические объекты. Для этого необходимо определить ключевые характеристики и параметры, описывающие объект или процесс, и выразить их с помощью математических символов и операций.
При построении математической модели необходимо учитывать различные факторы и условия, которые влияют на объект или процесс. Важно учесть все существенные детали и особенности, которые могут оказать влияние на модель. Также необходимо выбрать подходящую математическую структуру и методы, которые позволят решить задачу эффективно и точно.
Построение математической модели также требует проведения экспериментов, сбора данных и анализа полученных результатов. Это позволяет уточнить модель, учесть возможные ошибки и неточности, а также проверить ее достоверность и применимость.
В результате построения математической модели получается абстрактное представление реального объекта или процесса, которое позволяет проводить различные исследования, прогнозировать поведение системы, оптимизировать процессы и принимать решения на основе полученных результатов.
Оценка и анализ результатов моделирования
Во-первых, необходимо проверить, соответствуют ли результаты моделирования ожидаемым свойствам системы. Например, если модель описывает течение жидкости в трубе, то результаты моделирования должны быть согласованы с физическими законами, такими как закон сохранения массы и закон сохранения энергии.
Во-вторых, результаты моделирования могут быть оценены с помощью статистических метрик. Например, можно сравнить модельные значения с экспериментальными данными и вычислить среднеквадратичную ошибку или коэффициент детерминации. Это позволяет судить о точности модели и ее способности предсказывать поведение системы.
Кроме того, анализ результатов моделирования может включать в себя сравнение различных вариантов модели или рассмотрение влияния различных параметров на результаты. Например, можно изменить значения параметров модели и посмотреть, как это повлияет на ее поведение.
Важно отметить, что оценка и анализ результатов моделирования не являются одноразовой задачей. В процессе моделирования результаты могут быть уточнены и улучшены, и анализ должен проводиться на каждом этапе.
В заключение, оценка и анализ результатов моделирования позволяют оценить достоверность и адекватность модели, а также сделать выводы о поведении системы. Это важные шаги в процессе математического моделирования и помогают принять обоснованные решения на основе модельных данных.
Применение математического моделирования в различных областях
Физика
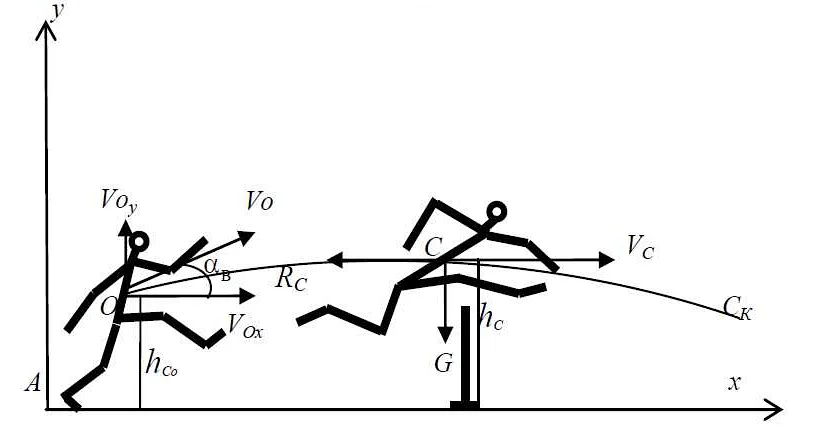
В физике математическое моделирование используется для создания моделей физических процессов и систем. Например, моделирование движения тела под действием силы гравитации позволяет предсказать его траекторию и скорость. Математическое моделирование также применяется в квантовой механике, теории относительности и других фундаментальных областях физики.
Биология

В биологии математическое моделирование используется для изучения различных биологических систем и процессов. Например, моделирование популяций позволяет предсказывать и анализировать изменения численности популяций живых организмов. Математическое моделирование также применяется в различных областях биологии, таких как генетика, нейробиология и эволюционная биология.
Социальные науки
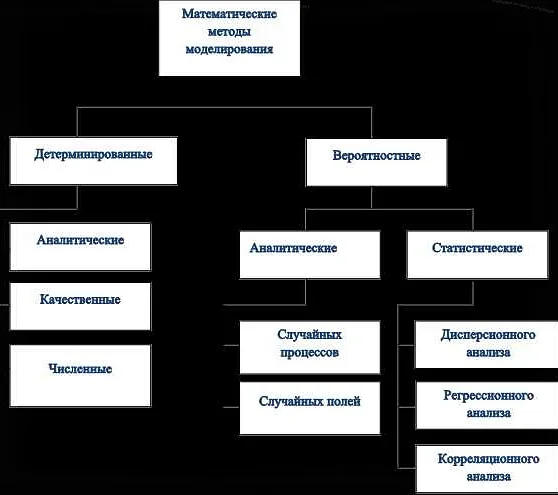
В социальных науках математическое моделирование используется для изучения различных социальных процессов и явлений. Например, моделирование распространения информации в социальных сетях может помочь предсказывать ее влияние на общественное мнение. Математическое моделирование также применяется в экономике, политологии и других областях социальных наук.
Технические науки
В технических науках математическое моделирование используется для разработки и оптимизации различных технических систем и процессов. Например, моделирование течения жидкости позволяет предсказывать ее поведение в различных условиях. Математическое моделирование также применяется в строительстве, компьютерной графике, проектировании электронных устройств и других областях технических наук.
Применение математического моделирования в различных областях позволяет углубить наше понимание сложных систем и процессов, предсказывать их поведение и разрабатывать эффективные стратегии и решения. Математическое моделирование является важным инструментом для развития науки, технологий и общества в целом.
Математическое моделирование в экономике
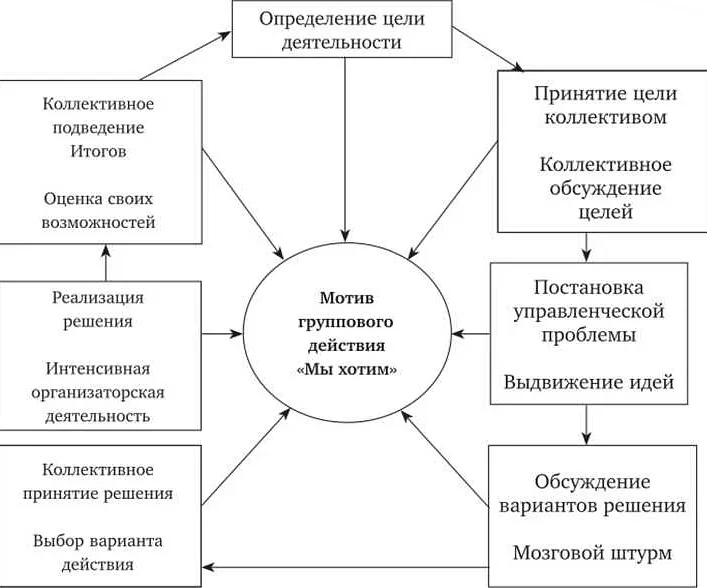
Основная цель математического моделирования в экономике — предоставить инструменты для анализа и оптимизации различных аспектов экономической деятельности. С его помощью можно исследовать влияние различных факторов на экономические процессы, прогнозировать будущие тенденции и оценивать эффективность различных стратегий и политик.
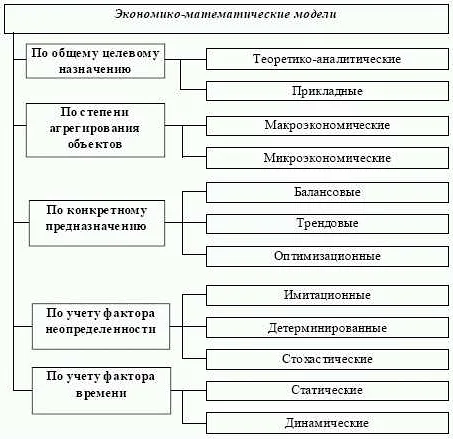
Математические модели экономики могут быть представлены в различных формах, включая дифференциальные уравнения, системы линейных и нелинейных уравнений, стохастические модели и другие. В зависимости от конкретной задачи, выбирается подходящий тип модели, который позволяет учесть особенности исследуемой экономической системы.
Применение математического моделирования в экономике широко распространено и используется во многих областях, включая макроэкономику, финансы, управление рисками, маркетинг и другие. Например, модели макроэкономического роста позволяют исследовать влияние различных экономических факторов на общую экономическую динамику страны. Математические модели финансовых рынков позволяют прогнозировать цены на акции и другие финансовые инструменты, а также оценивать риски и разрабатывать стратегии инвестирования.
В целом, математическое моделирование в экономике предоставляет аналитический подход к изучению и пониманию экономических процессов. Оно позволяет прогнозировать и анализировать различные сценарии развития экономики, оценивать эффективность политики и стратегий, а также принимать обоснованные решения на основе математических данных и анализа. Благодаря математическому моделированию экономика может стать более предсказуемой и управляемой.
Математическое моделирование в физике
Математическое моделирование в физике может быть применено в различных областях, начиная от механики и электродинамики, и заканчивая квантовой физикой и статистической физикой. Оно позволяет изучать движение тел, взаимодействие частиц, распространение волн и многое другое.
В основе математического моделирования в физике лежит использование уравнений и законов, описывающих физические явления. Эти уравнения могут быть дифференциальными, интегральными или алгебраическими. С их помощью строятся математические модели, которые позволяют предсказывать и анализировать поведение системы в различных условиях.
Процесс математического моделирования в физике включает несколько этапов. Сначала формулируется физическая задача и определяются граничные условия. Затем выбирается математическая модель, которая наилучшим образом описывает систему, и составляются соответствующие уравнения. После этого проводятся численные расчеты и анализ полученных результатов.
Математическое моделирование в физике играет важную роль в научных исследованиях и промышленности. С его помощью можно предсказывать и оптимизировать процессы, разрабатывать новые материалы и устройства, исследовать сложные физические явления и создавать новые теории.
Математическое моделирование в биологии
Математическое моделирование играет важную роль в биологии, позволяя исследователям изучать сложные процессы, которые происходят в живых организмах. Биологические системы обладают большой сложностью, и понимание их работы требует использования математических моделей. Математическое моделирование позволяет установить связи между различными компонентами биологической системы и предсказывать ее поведение в различных условиях.
Одной из основных задач математического моделирования в биологии является описание динамики изменения популяций организмов. Моделирование позволяет исследовать взаимодействие между популяциями, предсказывать изменения их численности во времени и прогнозировать влияние различных факторов на эти процессы. Такие модели могут быть полезными для понимания динамики распространения заболеваний, оценки эффективности мер по контролю популяций вредных организмов и разработки стратегий сохранения биоразнообразия.
Математическое моделирование также используется для изучения физиологических процессов, которые происходят в организмах. Например, моделирование позволяет исследовать динамику концентрации веществ в органах и тканях, определять оптимальные дозы лекарственных препаратов и прогнозировать их воздействие на организм. Такие модели помогают улучшить понимание физиологических механизмов и разработать новые методы диагностики и лечения различных заболеваний.
Кроме того, математическое моделирование используется для изучения эволюционных процессов. Моделирование позволяет исследовать изменения генетического состава популяции во времени, оценивать влияние различных факторов на эволюцию и предсказывать ее результаты. Такие модели могут быть полезными для понимания процессов специации, адаптации и распространения организмов.
В заключение, математическое моделирование является мощным инструментом для изучения биологических систем. Оно позволяет исследовать сложные процессы, предсказывать их поведение и разрабатывать стратегии управления биологическими системами. Математическое моделирование в биологии является незаменимым инструментом для развития нашего понимания живых организмов и их взаимодействия с окружающей средой.
Вопрос-ответ:
Какие методы математического моделирования существуют?
Существует множество методов математического моделирования, включая аналитические методы, численные методы и статистические методы. Аналитические методы основаны на использовании аналитических выражений и формул для построения моделей. Численные методы применяются для решения сложных математических задач с использованием компьютерных алгоритмов. Статистические методы используются для анализа данных и построения статистических моделей.
Какие принципы лежат в основе математического моделирования?
Основными принципами математического моделирования являются абстракция, упрощение и формализация. Абстракция позволяет выделить основные характеристики объекта и игнорировать незначительные детали. Упрощение позволяет представить сложный объект или явление в упрощенной форме. Формализация предполагает представление модели в виде математических уравнений и формул.
В каких областях применяются методы математического моделирования?
Методы математического моделирования широко применяются во многих областях, включая физику, химию, биологию, экономику, финансы, инженерные науки, компьютерные науки и т.д. Они используются для изучения и прогнозирования различных явлений и процессов, а также для оптимизации систем и принятия решений.
Какую роль играет математическое моделирование в научных исследованиях?
Математическое моделирование играет важную роль в научных исследованиях. Оно позволяет ученым изучать сложные явления и процессы, которые трудно или невозможно изучать экспериментально. Моделирование позволяет строить гипотезы, проверять их на соответствие экспериментальным данным и делать прогнозы. Оно также позволяет оптимизировать эксперименты и сократить затраты на их проведение.
Какие методы математического моделирования существуют?
Существуют различные методы математического моделирования, включая аналитическое моделирование, численное моделирование и статистическое моделирование. Аналитическое моделирование основано на использовании аналитических методов для построения математических моделей и получения точных аналитических решений. Численное моделирование основано на использовании численных методов для решения математических моделей, которые не имеют аналитического решения. Статистическое моделирование используется для анализа статистических данных и прогнозирования будущих событий.
Какие принципы лежат в основе математического моделирования?
Основные принципы математического моделирования включают выбор подходящей математической модели, сбор данных для построения модели, определение параметров модели, проверку модели на соответствие эмпирическим данным и использование модели для прогнозирования или анализа. Также важными принципами являются учет неопределенности и изменчивости данных, проверка модели на чувствительность к изменениям параметров и валидация модели на независимых данных.
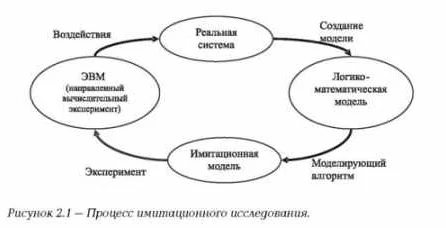

Статья очень интересная и полезная. Математическое моделирование – это процесс создания абстрактного математического описания реальной системы, что позволяет анализировать ее свойства и поведение. Этот подход является основой для решения многих задач в науке, технике и экономике. Математические модели помогают прогнозировать результаты сложных процессов, оптимизировать ресурсы, исследовать новые технологии. Они позволяют снизить затраты, ускорить процессы и повысить эффективность. Например, моделирование климата помогает прогнозировать глобальные изменения, а моделирование экономики – предсказывать развитие мировых финансовых рынков. Математическое моделирование – это очень мощный инструмент, который продолжает развиваться и находить все большее применение в различных областях человеческой деятельности.