Что такое радианы в математике

Радианы — это единица измерения угла в математике, которая используется для измерения углов в круге. Они являются более удобными и естественными для многих математических операций, чем градусы. Узнайте, как конвертировать градусы в радианы и научитесь работать с радианами в математических вычислениях.

Радианы — это мера угла в геометрии и тригонометрии, которая широко применяется для измерения углов и вычисления дуг на окружности. Радианы являются одним из основных способов измерения углов, наряду с градусами.

Определение радиана основано на соотношении между длиной дуги окружности и радиусом этой окружности. Радианное измерение угла основывается на том факте, что длина дуги, равной радиусу окружности, равна одному радиану.

Формула для вычисления радианной меры угла определяется отношением длины дуги к радиусу окружности. Таким образом, радианная мера угла равна отношению длины дуги к радиусу:

радианы = длина дуги / радиус окружности

Радианы широко используются в математике и физике для решения различных задач, связанных с геометрией и тригонометрией. Они позволяют более точно измерить и описать углы и дуги на окружности, а также упростить вычисления и формулы в этих областях.

Что такое радианы?

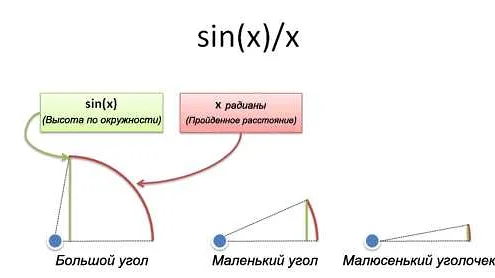
Радиан – это угол, при котором длина дуги окружности равна радиусу этой окружности. Другими словами, радиан – это отношение длины дуги окружности к её радиусу. Обозначается символом «рад».

Формула для перевода угла из градусов в радианы: радианы = (градусы * π) / 180, где π (пи) – математическая константа, равная примерно 3.14159.

Использование радианов в математике позволяет упростить многие вычисления, особенно в тригонометрии и анализе функций. Радианы также широко используются в физике при описании колебаний, вращательного движения и других явлений.

Примеры использования радианов: измерение углов в тригонометрии (например, синусы, косинусы), расчёт длины дуги окружности и площади сектора, определение периода и частоты колебаний.

Определение радианов в математике

Один радиан соответствует центральному углу, под которым длина дуги равна радиусу окружности. Таким образом, если длина дуги равна радиусу, то угол, под которым эта дуга видна из центра окружности, равен 1 радиану.

Формула для вычисления радианов:

1. Узнайте длину дуги окружности.
2. Разделите длину дуги на радиус окружности.

Например, если длина дуги равна 10 см, а радиус окружности – 5 см, то радианы можно вычислить следующим образом:

1. Длина дуги: 10 см
2. Радиус окружности: 5 см
3. 10 см / 5 см = 2 радиана

Таким образом, угол, под которым видна эта дуга из центра окружности, равен 2 радианам.

Значение радиана в геометрии

Формула для вычисления значения радиана: радиан = длина дуги / радиус окружности.

Значение радиана представляет собой отношение длины дуги окружности к длине радиуса. Это означает, что если длина дуги окружности равна длине радиуса, то значение радиана будет равно 1.

В геометрии значение радиана используется для измерения углов. Например, если угол равен 1 радиану, это означает, что длина дуги окружности, которую охватывает этот угол, равна длине радиуса окружности.

Значение радиана также имеет важное значение при вычислении тригонометрических функций, таких как синус, косинус и тангенс. Тригонометрические функции определяются с помощью отношения сторон прямоугольного треугольника или отношения длин дуги и радиуса окружности.

В геометрии радиан является удобной единицей измерения угла, так как позволяет учесть как длину дуги, так и радиус окружности. Это позволяет более точно определить величину угла и использовать его в различных вычислениях.

Таким образом, значение радиана в геометрии играет важную роль при измерении углов и вычислении тригонометрических функций.

Как вычислить радианы?

Формула для вычисления радианов:

Угол в градусахУгол в радианах

180°	π
90°	π/2
60°	π/3
45°	π/4

Чтобы вычислить радианы для другого угла, необходимо разделить значение угла в градусах на 180 и умножить результат на π.

Например, чтобы вычислить радианы для угла 30°:

Радианы = (30° / 180) * π = 0.166π

Таким образом, радианы для угла 30° равны приблизительно 0.166π.

Формула для перевода градусов в радианы

Для перевода градусов в радианы существует простая формула:

• Чтобы перевести градусы в радианы, нужно умножить количество градусов на значение константы π (пи) и разделить полученное значение на 180.

Математически данная формула выглядит следующим образом:

радианы = (градусы * π) / 180

Где:

• радианы — значение в радианах;
• градусы — значение в градусах;
• π — математическая константа, приближенное значение которой равно 3.14159;
• 180 — количество градусов в полном круге.

Например, чтобы перевести 90 градусов в радианы, мы можем использовать данную формулу:

радианы = (90 * π) / 180 ≈ 1.5708

Таким образом, 90 градусов примерно равны 1.5708 радианам.

Формула для перевода градусов в радианы является важной в математике и используется в различных областях, включая тригонометрию, физику и инженерные расчеты.

Примеры вычислений радианов

Для того чтобы лучше понять, как работают радианы, рассмотрим несколько примеров.

Пример 1:

Допустим, у нас есть окружность радиусом 5 см. Найдем длину дуги, соответствующей углу в 90 градусов.

Формула длины дуги в радианах: длина дуги = радиус * угол в радианах

Угол в радианах можно найти, разделив значение угла в градусах на 180 и умножив на число пи (π).

Для угла в 90 градусов:

Угол в радианах = (90 / 180) * π = (1/2) * π

Длина дуги = 5 * (1/2) * π = 2.5π см

Пример 2:

Предположим, что у нас есть треугольник со сторонами 3 см, 4 см и 5 см. Найдем значение угла между сторонами длиной 3 см и 4 см в радианах.

Мы можем использовать формулу для нахождения косинуса угла:

косинус угла = (длина одной стороны ^ 2 + длина другой стороны ^ 2 — длина третьей стороны ^ 2) / (2 * длина одной стороны * длина другой стороны)

Для нашего треугольника:

косинус угла = (3 ^ 2 + 4 ^ 2 — 5 ^ 2) / (2 * 3 * 4) = (9 + 16 — 25) / 24 = 0

Так как косинус угла равен 0, значит угол равен 90 градусов (или π/2 радиан).

Это лишь некоторые примеры применения радианов в математике. Важно понимать, что радианы представляют собой удобную единицу измерения для работы с углами и находят широкое применение в различных областях науки и техники.

Зачем нужны радианы в математике?

Основное преимущество радианов заключается в том, что их использование позволяет более удобно и точно оперировать углами. В отличие от градусов, радианы позволяют проводить более сложные вычисления и получать более точные результаты.

Радианы также активно используются в тригонометрии, особенно при работе с тригонометрическими функциями, такими как синус, косинус и тангенс. Формулы, связанные с этими функциями, оказываются более удобными и понятными при использовании радианов.

Кроме того, радианы используются в физике, особенно при решении задач, связанных с колебаниями, волнами и круговыми движениями. Использование радианов позволяет более точно описывать и анализировать эти процессы, а также упрощает математические выкладки.

Таким образом, радианы являются неотъемлемой частью математики и физики, предоставляя удобный и точный способ измерения углов и решения различных задач.

Применение радианов в физике

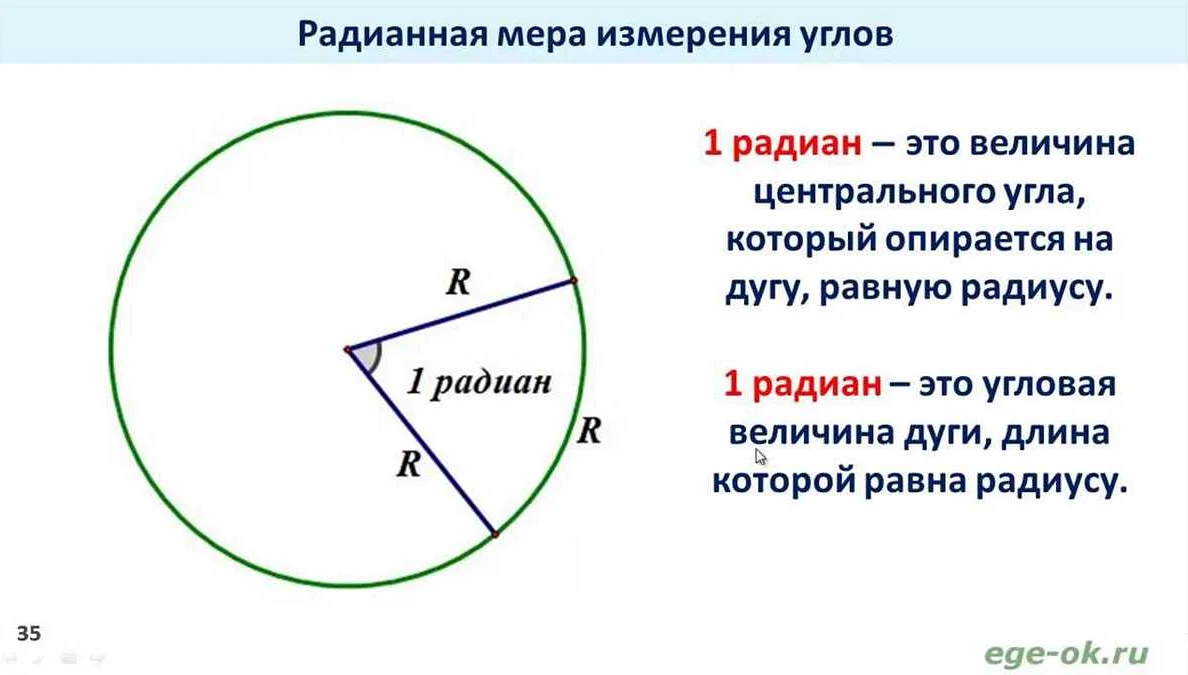
В физике радианы используются для описания угловых перемещений тела. Угол в радианах определяется отношением длины дуги окружности к радиусу этой окружности. Таким образом, величина угла в радианах равна отношению длины дуги к радиусу.

Радианы позволяют точнее описывать угол поворота тела, так как они не зависят от размеров или формы объекта. Это особенно важно при изучении вращательного движения, например, при анализе колебаний маятника или вращения рулетки.

В физике радианы также используются для измерения фазового угла при описании колебательных процессов. Фазовый угол показывает, насколько смещено колебание относительно начального положения и измеряется в радианах.

Кроме того, радианы используются при расчете траектории движения частицы в электромагнитном поле или при определении углового ускорения при вращении тела.

Таким образом, радианы играют важную роль в физике, позволяя более точно описывать угловые перемещения и колебательные процессы. Изучение и применение радианов в физике имеет большое значение для понимания различных физических явлений и является неотъемлемой частью математического аппарата физики.

Роль радианов в тригонометрии

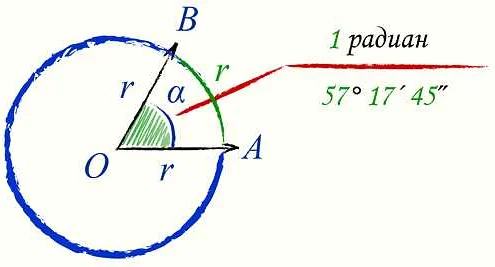
Радианы определяются как длина дуги, равной радиусу окружности. Измерение угла в радианах позволяет более точно работать с тригонометрическими функциями и упрощает математические вычисления.

Формула для перевода угла из градусов в радианы выглядит следующим образом:

Угол в радианах = Угол в градусах * (π / 180)

Здесь π (пи) представляет собой математическую константу, равную приблизительно 3,14159.

Пример использования радианов в тригонометрии:

Для нахождения значения синуса угла, заданного в радианах, необходимо использовать соответствующую тригонометрическую функцию. Например, если угол равен π/6, то значение синуса будет равно 0.5.

Таким образом, радианы играют важную роль в тригонометрии, облегчая вычисления и позволяя более точно работать с тригонометрическими функциями.

Вопрос-ответ:

Зачем в математике используют радианы?

Радианы — это единицы измерения угла в математике, которые широко используются для удобства и точности при работе с тригонометрическими функциями. Они позволяют избежать проблем, связанных с использованием других единиц измерения угла, таких как градусы. Радианы также имеют простое и понятное определение, что делает их удобными для использования в различных задачах.

Как определить радианы?

Радианы определяются как отношение длины дуги окружности к радиусу этой окружности. Для того чтобы определить угол в радианах, нужно разделить длину дуги окружности, которую охватывает этот угол, на радиус этой окружности. Таким образом, если длина дуги равна r, а радиус равен R, то угол в радианах равен r/R.

Как связаны радианы и градусы?

Существует простая формула для перевода радианов в градусы: угол в градусах равен углу в радианах, умноженному на 180 и поделенному на π. То есть, угол в градусах = угол в радианах * 180 / π. С помощью этой формулы можно легко переводить углы из одной системы измерения в другую.

Какие примеры использования радианов в математике?

Радианы используются во многих областях математики и физики. Например, они широко применяются в тригонометрии для изучения и решения задач, связанных с треугольниками и колебаниями. Также радианы используются в анализе функций, чтобы определить периодические закономерности и поведение функций. Еще одним примером использования радианов является расчет длины окружности и площади сектора окружности.

Можно ли использовать радианы для измерения отрицательных углов?

Да, радианы могут быть использованы для измерения отрицательных углов. Отрицательный угол в радианах определяется как угол, в котором начальная сторона охватывается направлением в отрицательном направлении. Например, если положительное направление охватывается против часовой стрелки, то отрицательный угол будет охватываться по часовой стрелке.

Что такое радианы в математике?

Радианы в математике — это единица измерения угла, которая считается наиболее удобной. Она определяется как длина дуги, равной радиусу окружности, на которой она находится.

Какая формула используется для перевода градусов в радианы?

Для перевода градусов в радианы используется формула: радианы = градусы * (пи/180).

Видео по теме: