Чем измеряют углы в математике

В математике углы измеряются в градусах, радианах и гонях. Градус — наиболее распространенная единица измерения углов, радиан — единица измерения, основанная на длине дуги окружности, а гон — единица измерения, используемая в артиллерии и навигации. Углы могут быть положительными и отрицательными, а их величина может быть выражена в виде числа или символа.

В математике углы являются одним из важнейших понятий. Они не только применяются в геометрии, но и широко используются во многих других науках и отраслях деятельности. Для измерения углов существуют различные способы, каждый из которых имеет свои особенности и преимущества.

Один из самых распространенных способов измерения углов — градусы. Градус является наиболее привычной единицей измерения угла и обозначается символом °. Основной окружностью для измерения углов в градусах является окружность, разделенная на 360 равных частей. Каждая часть называется градусом, а угол, равный 1/360 окружности, составляет один градус.

Кроме градусов, существуют и другие единицы измерения углов, такие как радианы, минуты и секунды. Радиан — это такая единица измерения угла, при которой длина дуги окружности равна радиусу. Один радиан соответствует углу, при котором длина дуги окружности равна радиусу. Радианы используются в основном в математических вычислениях и физике.

«Минуты» и «секунды» — это дополнительные единицы измерения углов, которые используются для более точного измерения. Минута является 1/60 градуса, а секунда — 1/60 минуты. Использование минут и секунд позволяет более точно измерять углы, особенно малые углы, такие как углы наклона.»

Знание различных способов измерения углов в математике позволяет более точно решать геометрические задачи и проводить различные исследования. Каждая единица измерения углов имеет свои достоинства и ограничения, и выбор конкретного способа измерения зависит от целей и задач, которые необходимо решить.

Что такое измерение углов?

Углы могут быть различных размеров и форм. Для удобства измерения углов в математике используются различные единицы измерения, такие как градусы, радианы, минуты и секунды.

Градусы – это наиболее распространенная единица измерения углов. Один полный оборот составляет 360 градусов. Градусы обозначаются символом °.

Радианы – это другая единица измерения углов. Один полный оборот составляет 2π радианов. Радианы обозначаются символом рад.

Минуты и секунды – это дополнительные единицы измерения углов, которые используются для более точного измерения. Одна минута составляет 1/60 градуса, а одна секунда составляет 1/60 минуты.

Измерение углов играет важную роль во многих областях, таких как геометрия, физика, инженерия и астрономия. Оно позволяет точно определить углы и использовать их в различных вычислениях и построениях.

Единица измеренияОбозначениеКоличество в одном полном обороте

Градусы	°	360
Радианы	рад	2π
Минуты	‘	60
Секунды	»	60

Зачем нам нужно измерять углы?

Одной из основных причин измерять углы является необходимость в точном описании направления и поворотов. Углы позволяют нам определить, как два отрезка или две плоскости соединяются, и как они изменяются при различных действиях. Это особенно важно в навигации, геодезии, архитектуре и строительстве, где точность и точное взаимное расположение объектов являются ключевыми факторами.

Измерение углов также необходимо в физике и инженерных науках. Углы помогают нам анализировать движение и силы, изучать поведение волн и света, а также прогнозировать и предсказывать различные физические явления. В механике, электронике и других областях, где требуется точное позиционирование и измерение, углы играют важную роль.

Кроме того, измерение углов имеет практическое применение в ежедневной жизни. Например, в строительстве и ремонте мы используем углы для создания прямых и перпендикулярных линий, для определения наклона поверхностей и геометрических фигур. Измерение углов также используется в спорте, например, в гольфе, бильярде и стрельбе из лука, где точность и контроль углов играют важную роль в достижении успеха.

Таким образом, измерение углов является неотъемлемой частью нашей жизни и позволяет нам лучше понимать и описывать окружающий мир. Оно находит применение в различных областях, от науки и инженерии до повседневных задач, и является необходимым инструментом для достижения точности, контроля и понимания.

Градусы

Градусы обозначаются символом «°» и обычно записываются перед числом, которое указывает величину угла. Например, угол в 45 градусов записывается как 45°.

Градусы удобны для измерения углов в повседневной жизни и в многих областях, таких как география, архитектура, физика, инженерное дело и многих других.

Также существует подразделение градусов на более мелкие единицы измерения — минуты и секунды. Каждая минута делится на 60 равных частей, называемых минутами (‘). Каждая минута делится на 60 равных частей, называемых секундами («).

Использование градусов позволяет нам более точно и удобно измерять углы и работать с ними в математике и других науках.

Что такое градусы?

Один градус обозначается символом °. Полный поворот вокруг точки составляет 360 градусов. Градусы могут быть разделены на более мелкие единицы, такие как минуты и секунды.

В таблице ниже приведены примеры углов, измеренных в градусах:

Угол (градусы)Обозначение

0	0°
90	90°
180	180°
270	270°
360	360°

Градусы широко используются в различных областях, таких как физика, геометрия, навигация и инженерия. Они помогают измерять и описывать углы и повороты объектов.

Как измерять углы в градусах?

Для измерения угла в градусах используют специальный инструмент — градусник или транспортир. Градусник имеет полукруглую шкалу, где 0 градусов соответствуют начальному положению инструмента, а 180 градусов — его конечному положению. Остальные значения углов можно измерить, поворачивая градусник в соответствующую сторону.

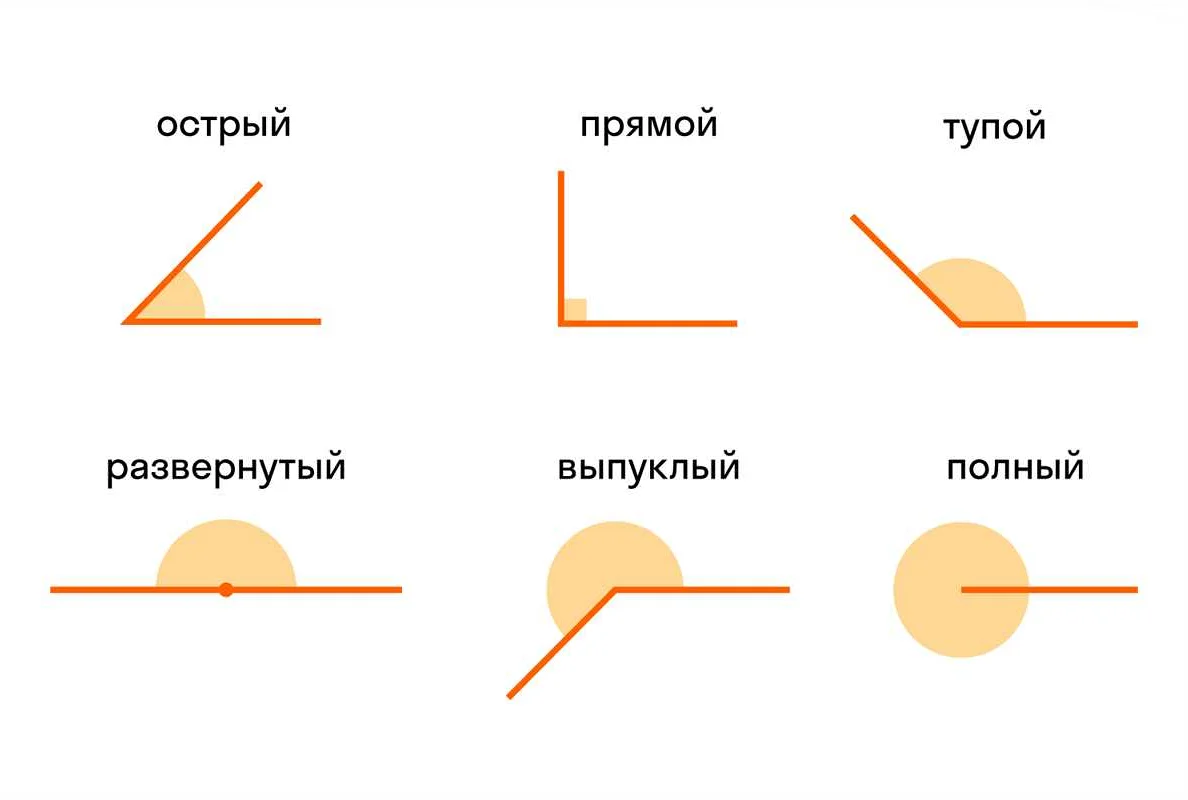
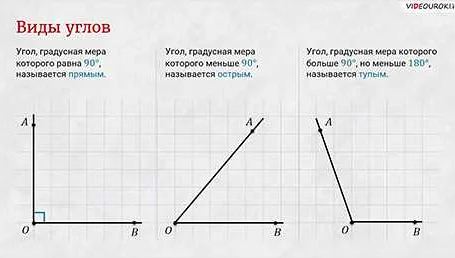
При измерении угла в градусах обычно используются такие термины, как острый угол (меньше 90 градусов), прямой угол (90 градусов), тупой угол (больше 90 градусов) и полный угол (равен 360 градусам).

Для записи угла в градусах используется символ ° после числового значения. Например, угол в 45 градусов записывается как 45°.

Измерение углов в градусах широко применяется в геометрии, физике, инженерии и других областях науки и техники. Это удобная система, которая позволяет легко определить и сравнивать углы в пространстве.

Радианы

В одном радиане содержится примерно 57,3 градусов. Для перевода угла из градусов в радианы необходимо умножить значение угла в градусах на π/180. Для перевода угла из радианов в градусы необходимо умножить значение угла в радианах на 180/π.

Радианы используются в математике и физике для удобства расчетов и формулирования законов и формул, особенно в теории функций и тригонометрии.

Угол в градусахУгол в радианах

0°	0
30°	π/6
45°	π/4
60°	π/3
90°	π/2
180°	π

Таким образом, радианы позволяют более точно и удобно измерять углы и использовать их в различных расчетах и формулах.

Что такое радианы?

Для того чтобы лучше понять, что такое радиан, рассмотрим пример. Представьте себе окружность радиусом 1. Если взять дугу длиной в радиус окружности, то эту дугу можно свернуть так, чтобы она стала линией. Получившаяся линия будет радианом. Таким образом, радиан — это длина дуги окружности, равная радиусу окружности.

УголРадианы

0°	0
30°	π/6
45°	π/4
60°	π/3
90°	π/2
180°	π
360°	2π

Радианы являются наиболее удобной единицей измерения углов в математике, так как они позволяют более просто и точно выражать углы и выполнять различные математические операции с ними. В отличие от градусов, радианы не зависят от размера окружности и позволяют более точно описывать углы.

Как измерять углы в радианах?

В радианах угол измеряется как отношение длины дуги, выраженной в радиусах, к радиусу окружности. Полный оборот окружности составляет 2π радиан, где π (пи) — математическая константа, примерное значение которой равно 3,14159.

Для преобразования угла из градусов в радианы можно воспользоваться формулой:

Угол в градусахУгол в радианах

0°	0
30°	π/6
45°	π/4
60°	π/3
90°	π/2
180°	π
360°	2π

Таким образом, для перевода угла из градусов в радианы нужно умножить значение угла в градусах на π/180.

Измерение углов в радианах широко используется в математике, физике и других науках, так как позволяет более точно описывать и анализировать различные процессы и явления.

Минуты

Минуты обозначаются символом «′» (апостроф) и часто используются для более точного измерения углов. Например, если угол равен 30 градусам, то он также может быть записан как 30° 0′.

Минуты дополнительно делятся на секунды. Одна минута равна 60 секундам. Секунды обозначаются символом «″» (двойной апостроф) и используются для еще более точного измерения углов. Например, угол в 30 градусов и 15 минут может быть записан как 30° 15′ 0″.

Использование минут и секунд позволяет более точно определить угол и его положение, особенно при работе с географическими координатами или в навигации.

УголГрадусыМинутыСекунды

30 градусов	30°	0′	0″
45 градусов	45°	0′	0″
90 градусов	90°	0′	0″

Таким образом, минуты и секунды позволяют более точно измерять углы и представлять их в удобной форме.

Что такое минуты в измерении углов?

Минуты обозначаются символом ‘. Например, угол, равный 45 градусам и 30 минутам, записывается как 45°30’. Для более точного измерения углов иногда используются еще более мелкие единицы измерения — секунды.

Минуты имеют важное значение при измерении углов, особенно в геометрии и навигации. Они позволяют точнее определить углы и установить требуемую точность в вычислениях. Также, использование минут и секунд углов облегчает контроль и передачу информации о навигационных координатах.

Вопрос-ответ:

Зачем нужны различные способы измерения углов?

Различные способы измерения углов используются для удобства и точности в различных областях математики, физики и других наук. Например, градусы часто используются в геометрии и геодезии, радианы — в тригонометрии и анализе, а минуты и секунды — в навигации и астрономии.

Как перевести градусы в радианы?

Для перевода градусов в радианы нужно умножить значение в градусах на \(\frac{\pi}{180}\). Например, чтобы перевести 45 градусов в радианы, нужно умножить 45 на \(\frac{\pi}{180}\) и получить значение равное около 0.785 радиан.

Как перевести радианы в градусы?

Для перевода радианов в градусы нужно умножить значение в радианах на \(\frac{180}{\pi}\). Например, чтобы перевести 1.57 радиан в градусы, нужно умножить 1.57 на \(\frac{180}{\pi}\) и получить значение равное около 90 градусов.

Чем отличаются минуты и секунды от градусов и радиан?

Минуты и секунды — это подразделения градусов. 1 градус равен 60 минутам, а 1 минута равна 60 секундам. Таким образом, 1 градус равен 3600 секундам. Минуты и секунды используются для более точного измерения углов, особенно в навигации и астрономии.

Можно ли использовать различные способы измерения углов одновременно?

Да, можно использовать различные способы измерения углов одновременно, особенно в сложных вычислениях и анализе. Например, в тригонометрии часто используются радианы, но иногда может потребоваться перевести результаты в градусы для более понятного представления. В таких случаях применяются соответствующие формулы для перевода значений.

Какие единицы измерения углов существуют в математике?

В математике существуют несколько единиц измерения углов: градусы, радианы, минуты и секунды. Градусы — это наиболее распространенная единица измерения углов, обозначается символом °. Радианы — это другая единица измерения углов, которая является более естественной для математических расчетов. Минуты и секунды — это подразделения градуса, обозначаются символами ‘ и ». Например, угол 45 градусов можно записать как 45° или как 45° 0’ 0».

Видео по теме: