Что такое равнодействующая сила в математике

Равнодействующая сила в математике — это векторная сумма всех сил, действующих на объект. Она позволяет определить общее действие всех сил на объект и его направление. Узнайте больше о понятии равнодействующей силы и ее применении в математике.

Равнодействующая сила – это физическая величина, используемая в математике для определения силы, которая может заменить систему сил и иметь тот же эффект на объект. В других словах, равнодействующая сила является суммой всех сил, действующих на объект, и она применяется для определения общего эффекта этих сил.

Понятие равнодействующей силы является важным для решения различных задач, связанных с динамикой и статикой объектов. Оно позволяет упростить анализ сложных систем сил и определить результат их воздействия на объект.

Применение равнодействующей силы распространено во многих областях науки и техники. Например, в механике, равнодействующая сила используется для определения движения объектов под воздействием нескольких сил. В аэродинамике, равнодействующая сила применяется для анализа силы, возникающей при движении объектов в воздухе.

Использование равнодействующей силы позволяет не только более эффективно анализировать системы сил, но и предсказывать результаты их воздействия на объекты. Это важное понятие позволяет инженерам и ученым оптимизировать проектирование и разработку различных устройств и механизмов.

В заключение, равнодействующая сила играет важную роль в математике и науке. Она позволяет определить общий эффект системы сил и упростить анализ их воздействия на объекты. Применение равнодействующей силы в различных областях науки и техники позволяет предсказывать результаты воздействия и оптимизировать процессы разработки и проектирования.

Что такое равнодействующая сила?

Равнодействующая сила может быть положительной или отрицательной, в зависимости от направления и величины других сил. Если все силы направлены в одну сторону, равнодействующая сила будет равна их алгебраической сумме. Если силы направлены в противоположные стороны, равнодействующая сила будет разностью их алгебраической суммы.

Применение равнодействующей силы позволяет упростить анализ и вычисления в задачах, связанных с механикой и динамикой объектов. Она позволяет учитывать все взаимодействующие силы как одну общую, упрощая расчеты и предоставляя более наглядное представление о состоянии объекта.

Математическое определение равнодействующей силы

Математическое определение равнодействующей силы может быть записано следующим образом:

• • Если силы действуют в одной плоскости, то равнодействующая сила равна векторной сумме всех сил:

$$\vec{F}_{\text{р}}=\vec{F}_1+\vec{F}_2+…+\vec{F}_n$$

• • Если силы действуют в разных плоскостях, то равнодействующая сила находится путем разложения каждой силы на компоненты и их сложения:

$$\vec{F}_{\text{р}}=\vec{F}_{\text{р}_x}+\vec{F}_{\text{р}_y}+\vec{F}_{\text{р}_z}$$

Где:

• $$\vec{F}_{\text{р}}$$ — равнодействующая сила
• $$\vec{F}_1, \vec{F}_2, …, \vec{F}_n$$ — исходные силы
• $$\vec{F}_{\text{р}_x}, \vec{F}_{\text{р}_y}, \vec{F}_{\text{р}_z}$$ — компоненты равнодействующей силы по осям $$x, y, z$$ соответственно

Математическое определение равнодействующей силы позволяет удобно вычислять и анализировать общее воздействие всех сил на тела или системы тел, что является важным в механике и других областях, где изучаются силы и движение.

Способы вычисления равнодействующей силы

Существует несколько способов вычисления равнодействующей силы:

1. Графический метод. В данном методе силы представляются в виде векторов, их масштабируют и изображают на графической плоскости. Затем проводятся операции сложения векторов, чтобы получить равнодействующую силу. Результирующий вектор равнодействующей силы будет иметь направление и величину, определяемые суммой векторов.

2. Аналитический метод. В аналитическом методе силы представляются в виде векторов с известными координатами. Затем применяются методы аналитической геометрии и алгебры, такие как сложение векторов, для нахождения равнодействующей силы. Результирующая сила может быть представлена в виде уравнения с известными коэффициентами.

3. Метод разложения на составляющие. Этот метод основан на том, что любую силу можно представить в виде суммы сил, действующих в разных направлениях. Затем находятся равнодействующие силы в каждом направлении и их компоненты складываются для получения равнодействующей силы. Этот метод особенно полезен, когда система сил действует в нескольких разных направлениях.

4. Метод численных вычислений. В этом методе силы и их воздействие на систему представляются в виде численных значений. Затем применяются численные методы, такие как метод наименьших квадратов или метод Эйлера, для вычисления равнодействующей силы. Этот метод может быть полезен, когда имеется большое количество сил и точные аналитические вычисления затруднительны.

В зависимости от условий задачи и доступных данных, можно выбирать наиболее удобный способ вычисления равнодействующей силы. Правильное определение равнодействующей силы является важным шагом для анализа и решения задач механики.

Формула равнодействующей силы

Формула равнодействующей силы может быть записана как:

1. Если силы действуют вдоль одной оси:
   Равнодействующая сила (Fр) = F1 + F2 + … + Fn
2. Если силы действуют в разных направлениях:
   Равнодействующая сила (Fр) = √(F12 + F22 + … + Fn2)

В первом случае силы суммируются по модулю, а во втором случае силы суммируются по теореме Пифагора. Результатом будет величина равнодействующей силы, которая определяет направление и силу действия на объект.

Формула равнодействующей силы является основным инструментом для анализа и решения множества задач в механике и физике. Она позволяет определить, какие силы действуют на объект и как они влияют на его движение или состояние равновесия.

Примеры применения равнодействующей силы в реальной жизни

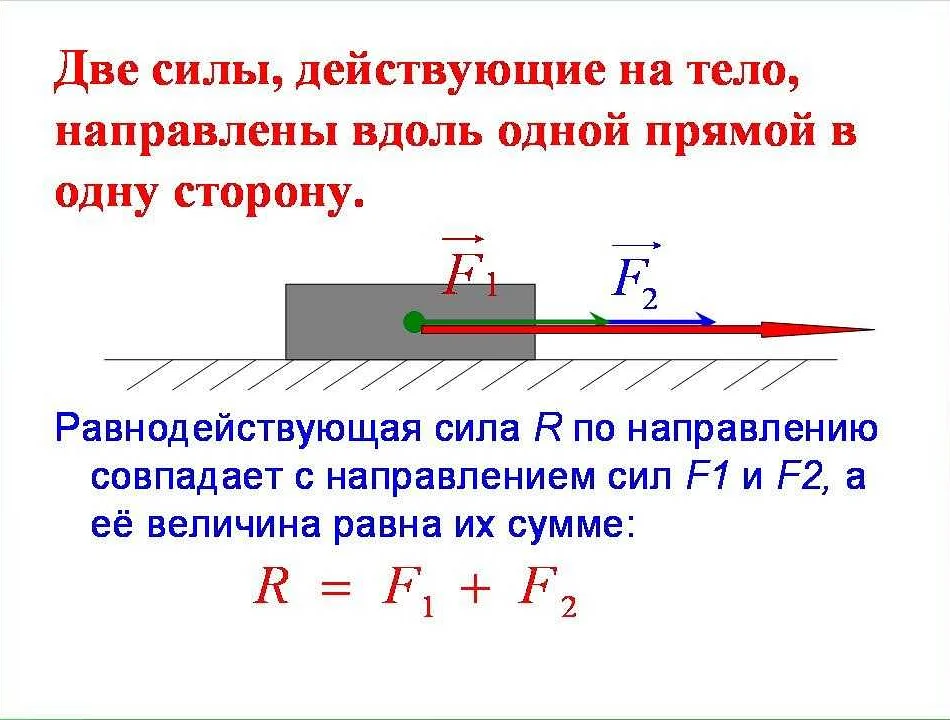
Автомобильная индустрия:

В автомобильной индустрии равнодействующая сила играет важную роль при разработке и проектировании автомобилей. При движении автомобиля различные силы, такие как сила трения, аэродинамическое сопротивление и сила тяги, действуют на него. Равнодействующая сила позволяет определить общую силу, необходимую для перемещения автомобиля, а также его устойчивость на дороге.

Строительство:

В строительстве равнодействующая сила используется для расчета нагрузок на конструкции зданий и сооружений. Например, при проектировании мостов или высотных зданий, равнодействующая сила позволяет определить необходимые размеры и прочность конструкции, чтобы она выдерживала все силы, действующие на нее, включая силу гравитации и воздействие ветра.

Аэрокосмическая промышленность:

В аэрокосмической промышленности равнодействующая сила используется при проектировании и испытаниях ракет и космических аппаратов. Она помогает определить необходимую силу тяги для достижения нужной скорости и высоты, а также обеспечить устойчивость и безопасность полета.

Спорт:

В спорте равнодействующая сила играет важную роль в различных дисциплинах. Например, в футболе равнодействующая сила позволяет футболисту определить силу удара, чтобы достичь желаемого направления и скорости мяча. В боевых искусствах равнодействующая сила используется для определения силы удара и эффективности техники.

Механика:

В механике равнодействующая сила используется для решения различных задач. Например, при расчете момента силы на вращающемся объекте или при определении равновесия системы сил.

Примеры применения равнодействующей силы в реальной жизни демонстрируют важность этого концепта в различных областях, где требуется анализ и определение общей силы, действующей на объекты и системы.

Значение равнодействующей силы для статики

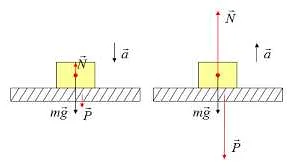
При анализе статического равновесия тела, равнодействующая сила играет особую роль. Если равнодействующая сила равна нулю, то тело находится в состоянии равновесия. Это означает, что все действующие на тело силы компенсируют друг друга и нет никакого движения или изменения состояния тела.

Определение равнодействующей силы позволяет упростить анализ силовых систем. Вместо изучения каждой отдельной силы, можно рассматривать только их равнодействующую силу и изучать ее свойства и взаимодействие с другими силами.

Значение равнодействующей силы для статики можно вычислить путем суммирования всех действующих на тело сил. Для этого необходимо учитывать направление и величину каждой силы, чтобы правильно определить равнодействующую силу.

Важно отметить, что равнодействующая сила является векторной величиной, то есть она имеет как направление, так и величину. Это позволяет учитывать не только величину каждой силы, но и их направление, что позволяет проводить более точные расчеты и анализировать взаимодействие сил в системе.

Расчет равнодействующей силы в динамике

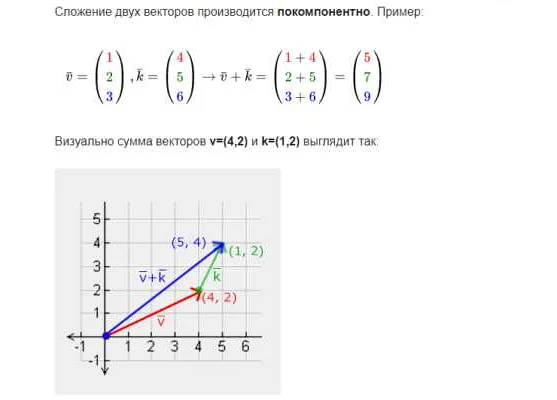
Для расчета равнодействующей силы необходимо учесть все силы, действующие на тело. Каждая сила должна быть представлена в виде вектора, который имеет направление и величину.

Для нахождения равнодействующей силы необходимо сложить все векторы сил. Для этого можно использовать правило параллелограмма или метод разложения силы на составляющие.

Правило параллелограмма гласит, что равнодействующая сила представляет собой диагональ параллелограмма, построенного на двух векторах сил. Для этого необходимо провести векторы сил из общей точки и построить параллелограмм по сторонам этих векторов. Диагональ параллелограмма будет равна равнодействующей силе.

Метод разложения силы на составляющие позволяет разбить вектор силы на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая определяет силу, действующую по горизонтали, а вертикальная составляющая – по вертикали. Затем необходимо сложить горизонтальные составляющие и вертикальные составляющие отдельно, чтобы получить равнодействующую силу.

Расчет равнодействующей силы в динамике является важным этапом для определения движения тела и его ускорения. Точное определение равнодействующей силы позволяет предсказать поведение тела в пространстве и применить соответствующие законы динамики для описания его движения.

Выводы о значении равнодействующей силы в математике

Основные выводы о значении равнодействующей силы:

1. Равнодействующая сила позволяет определить общую силу, действующую на тело. Это особенно важно при решении задач на динамику, где необходимо знать силы, действующие на тело со всех сторон.
2. Равнодействующая сила позволяет определить направление общей силы, действующей на тело. Это помогает в понимании, как будет двигаться тело под воздействием всех действующих на него сил.
3. Равнодействующая сила может быть равна нулю, если силы, действующие на тело, компенсируют друг друга.
4. Равнодействующая сила может быть использована для расчета ускорения тела. По второму закону Ньютона, ускорение тела пропорционально равнодействующей силе и обратно пропорционально массе тела.
5. Равнодействующая сила может быть разложена на составляющие по осям координат. Это позволяет анализировать силы, действующие на тело по отдельности и вносить корректировки в расчеты.

Выводы о значении равнодействующей силы в математике позволяют более точно и систематично решать задачи на динамику, обработку силовых систем и анализ движения тел. Понимание роли равнодействующей силы дает возможность предсказывать и объяснять физические явления на основе математических моделей.

Вопрос-ответ:

Что такое равнодействующая сила?

Равнодействующая сила — это сила, которая заменяет несколько других сил, действующих на тело, и имеет тот же эффект, что и все эти силы вместе.

Как вычислить равнодействующую силу?

Чтобы вычислить равнодействующую силу, необходимо сложить векторы сил, действующих на тело, по правилу сложения векторов. Полученный вектор будет равнодействующей силой.

Где применяется понятие равнодействующей силы?

Понятие равнодействующей силы применяется в физике и инженерии при исследовании движения тел. Это позволяет сократить количество сил, которые нужно учитывать при анализе системы, и упрощает расчеты.

Какие свойства имеет равнодействующая сила?

Равнодействующая сила обладает такими свойствами, как направление, величина и точка приложения. Направление равнодействующей силы определяется векторным сложением направлений исходных сил. Величина равнодействующей силы равна модулю векторной суммы исходных сил. Точка приложения равнодействующей силы совпадает с точкой приложения одной из исходных сил.

Как можно проиллюстрировать применение равнодействующей силы на практике?

Примером применения равнодействующей силы является тяга на веревке, к которой прикреплен груз. Если на веревку действуют две силы, направленные в разные стороны, то равнодействующая сила будет определять направление и величину движения груза.

Что такое равнодействующая сила?

Равнодействующая сила — это сумма всех действующих на объект сил. Она указывает на общую силу, которая действует на объект и определяет его движение или состояние покоя.

Видео по теме: