Что такое равновероятные события в математике примеры

Равновероятные события в математике — это события, которые имеют одинаковую вероятность выпадения. В статье приведены примеры равновероятных событий и объяснение их свойств в математике.

В математике существует понятие равновероятных событий, которое является одним из основных и важных для изучения вероятностей. Равновероятные события — это те события, которые обладают одинаковой вероятностью наступления. То есть, каждое из них имеет одинаковый шанс произойти, и вероятность каждого события равна 1/n, где n — количество равновероятных событий.

Примером равновероятных событий может служить бросок правильной монетки. В данном случае, у нас есть два равновероятных исхода: выпадение герба или выпадение решки. Оба этих исхода имеют одинаковую вероятность — 1/2. То есть, шансы выпадения герба или решки одинаковы и равны 50%.

Еще одним примером равновероятных событий может служить бросок справедливой игральной кости. В данном случае, у нас есть шесть равновероятных исходов: выпадение любой из шести граней игральной кости. Вероятность каждого из этих исходов равна 1/6, так как шансы выпадения каждой грани равны.

Важно понимать, что равновероятные события не всегда являются равноценными событиями. Равновероятные события могут иметь различное значение и влиять на итоговый результат. Например, в игре в рулетку, у нас есть 18 равновероятных событий (красное или черное), но это не означает, что вероятность выиграша при ставке на красное и черное будет одинакова. Это связано с наличием зеленого сектора на рулетке, который делает вероятность выигрыша неравной для красного и черного.

Определение равновероятных событий

Например, если мы бросаем правильную шестигранную игральную кость, то вероятность выпадения каждой из шести граней равна 1/6. Таким образом, события «выпадение 1», «выпадение 2», «выпадение 3» и так далее до «выпадения 6» являются равновероятными.

Также, равновероятные события могут быть у абстрактных моделей, например, при подбрасывании монеты. В этом случае, вероятность выпадения орла и решки равна 1/2, поскольку у нас есть два равновероятных исхода.

Определение равновероятных событий в математике позволяет строить модели и решать задачи, основываясь на вероятностных расчетах. Это важный элемент в области теории вероятностей и статистики, который находит применение не только в математике, но и в других науках и практических областях.

Примеры равновероятных событий

ПримерОбъяснение

Бросок монеты	Если монета справедливая, то вероятность выпадения орла и решки равна 0.5. Таким образом, орел и решка — равновероятные события.
Бросок игральной кости	Если игральная кость справедливая, то вероятность выпадения каждого числа от 1 до 6 равна 1/6. Таким образом, каждое число — равновероятное событие.
Выбор карты из колоды	Если колода содержит 52 карты и они перемешаны, то вероятность выбрать любую карту равна 1/52. Таким образом, выбор каждой карты — равновероятное событие.

Это только некоторые примеры равновероятных событий. В реальной жизни много ситуаций, где можно рассматривать различные равновероятные события, и математика помогает нам их изучать и анализировать.

Вероятность равновероятных событий

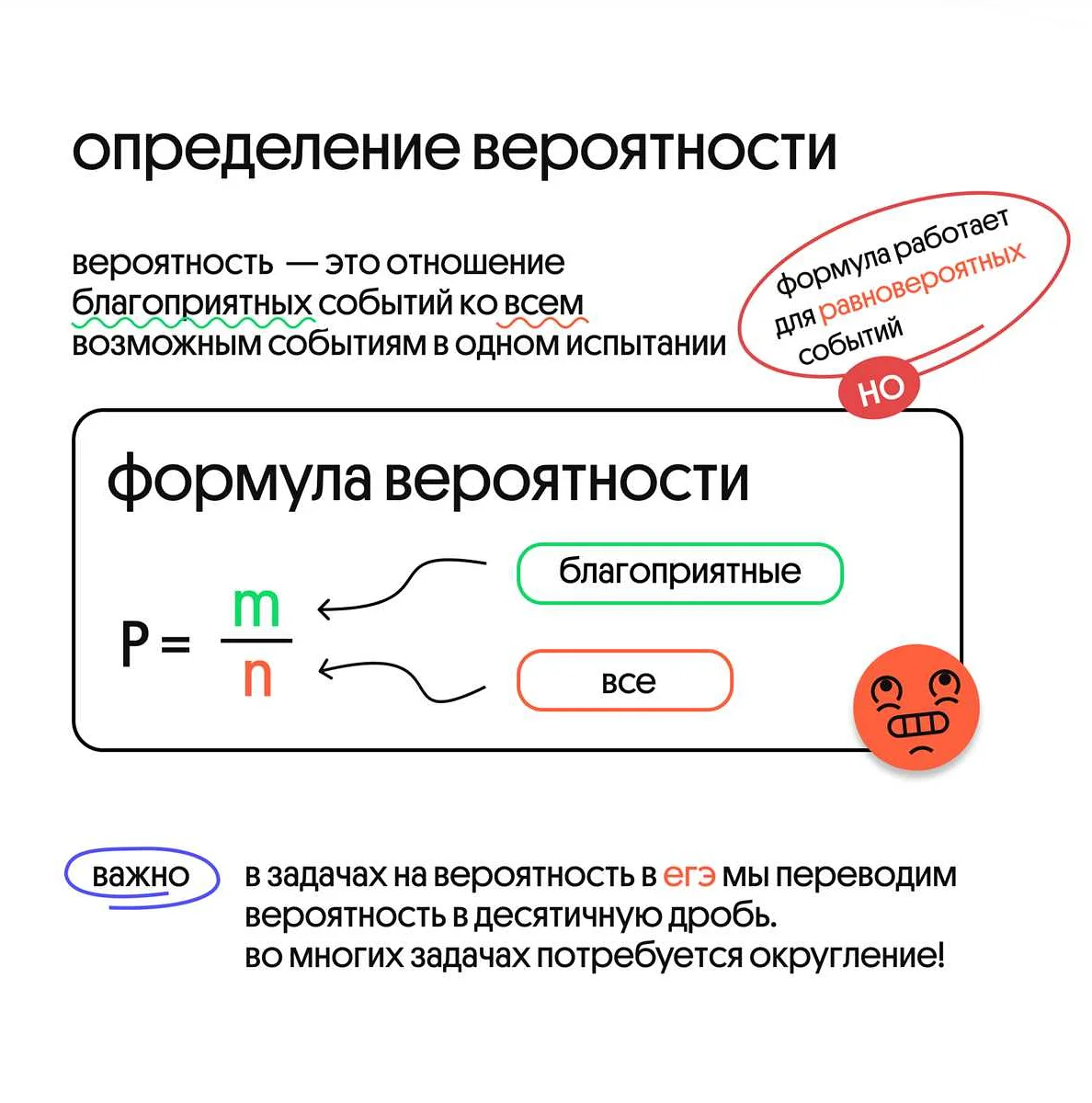
Для вычисления вероятности равновероятных событий необходимо знать общее количество возможных исходов и количество благоприятных исходов для каждого события. Затем вероятность каждого события вычисляется как отношение количества благоприятных исходов к общему количеству возможных исходов.

Например, если имеется монета, которая может выпасть либо орлом, либо решкой, то вероятность выпадения орла и решки равна 0,5 каждому из вариантов. Это происходит потому, что общее количество возможных исходов (2) равно количеству благоприятных исходов (1 для орла и 1 для решки).

Вероятность равновероятных событий может быть выражена числовыми значениями от 0 до 1, где 0 означает невозможность события, а 1 — его полную уверенность. Вероятность равновероятных событий всегда суммируется до 1, что означает, что одно из событий обязательно произойдет.

Определение вероятности равновероятных событий является важной концепцией в теории вероятностей и находит применение в различных областях, таких как статистика, физика, экономика и другие.

Сумма вероятностей равновероятных событий

Предположим, у нас есть n равновероятных событий, обозначим их как A1, A2, …, An. Тогда вероятность каждого события будет равна 1/n.

Сумма вероятностей всех равновероятных событий будет равна:

• P(A1) + P(A2) + … + P(An) = 1/n + 1/n + … + 1/n = n * (1/n) = 1.

Таким образом, сумма вероятностей всех равновероятных событий всегда равна 1.

Зависимость и независимость равновероятных событий

Зависимость и независимость равновероятных событий в математике играют важную роль при решении различных задач. Зависимость означает, что наступление одного события влияет на вероятность наступления другого события, тогда как независимость подразумевает, что наступление одного события не влияет на вероятность наступления другого события.

Для того чтобы определить зависимость или независимость событий, необходимо рассмотреть их вероятности в отдельности и в совокупности. Если вероятность наступления двух событий A и B вместе равна произведению вероятности наступления каждого из них по отдельности, то события A и B считаются независимыми. Формально это записывается как:

P(A и B) = P(A) * P(B)

Если же вероятность наступления двух событий вместе отличается от произведения вероятностей наступления каждого из них по отдельности, то события A и B считаются зависимыми.

Например, рассмотрим случай броска двух игральных костей. Пусть событие A заключается в том, что выпадет четное число на первой кости, а событие B — в том, что выпадет число больше 3 на второй кости. Вероятность наступления события A равна 1/2, так как на игральной кости 3 четных и 3 нечетных числа. Вероятность наступления события B также равна 1/2, так как на игральной кости 3 числа больше 3 и 3 числа меньше или равны 3. Вероятность наступления обоих событий A и B вместе равна 1/4, так как только две комбинации удовлетворяют обоим условиям: (2, 4) и (4, 4). Произведение вероятностей наступления каждого из событий по отдельности равно 1/2 * 1/2 = 1/4. Таким образом, события A и B являются независимыми.

Важно отметить, что зависимость или независимость событий не зависит от их равновероятности. Даже если события имеют разную вероятность, они могут быть зависимыми или независимыми в зависимости от условий задачи.

Видео по теме:

Вопрос-ответ:

Что такое равновероятные события?

Равновероятные события — это такие события, которые имеют одинаковую вероятность наступления. Вероятность каждого из этих событий равна 1/n, где n — количество равновероятных событий.

Как найти вероятность равновероятного события?

Чтобы найти вероятность равновероятного события, нужно разделить единицу на количество равновероятных событий. Например, если у нас есть 3 равновероятных события, то вероятность каждого из них будет равна 1/3.

Какие примеры равновероятных событий можно привести?

Примерами равновероятных событий могут быть: подбрасывание справедливой монеты (вероятность выпадения орла или решки равна 1/2), бросок справедливого игрального кубика (вероятность выпадения каждой из шести граней равна 1/6), выбор одной карты из колоды в 52 карты (вероятность выпадения каждой карты равна 1/52).

Какие свойства имеют равновероятные события?

Равновероятные события обладают рядом свойств. Во-первых, сумма вероятностей всех равновероятных событий равна единице. Во-вторых, вероятность наступления объединения нескольких равновероятных событий равна сумме вероятностей этих событий. В-третьих, вероятность наступления пересечения нескольких равновероятных событий равна произведению вероятностей этих событий.

Что делать, если события не являются равновероятными?

Если события не являются равновероятными, то для нахождения вероятности каждого из них нужно использовать другие методы, такие как классическое определение вероятности, относительная частота или статистические данные.

Что такое равновероятные события?

Равновероятные события – это события, которые имеют одинаковую вероятность наступления.

Какие примеры равновероятных событий можно привести?

Примерами равновероятных событий могут быть бросание обычной игральной кости (вероятность выпадения каждой из шести граней равна 1/6), выбор случайной карты из колоды (вероятность каждой карты равна 1/52), подбрасывание монеты (вероятность выпадения орла или решки равна 1/2) и т.д.

Равновероятные события и классическое определение вероятности

Классическое определение вероятности основано на предположении, что все исходы эксперимента равновероятны. То есть, если у нас есть n равновероятных исходов, а m из них благоприятствуют наступлению события A, то вероятность наступления события A можно определить как отношение m к n:

P(A) =

m

/

n

Например, если мы бросаем симметричную монету, то у нас есть два равновероятных исхода: орёл и решка. Таким образом, вероятность выпадения орла или решки равна 1/2.

Классическое определение вероятности широко используется в математике и статистике для расчёта вероятности наступления событий в различных случаях. Однако, оно не всегда применимо, так как в реальной жизни не все исходы эксперимента равновероятны.

Применение равновероятных событий в решении задач

Равновероятные события играют важную роль в решении различных задач в математике и статистике. Причина в том, что когда события равновероятны, то вероятность каждого из них равна и легко вычисляется.

Одним из примеров применения равновероятных событий является бросок честной монеты. В этом случае есть два равновероятных события: выпадение «орла» и выпадение «решки». Вероятность каждого из этих событий равна 1/2.

Если нужно решить задачу, связанную с броском монеты, можно использовать равновероятные события для упрощения вычислений. Например, если нужно найти вероятность того, что при трех бросках монеты выпадет два «орла», можно использовать комбинаторику и равновероятные события.

Другим примером применения равновероятных событий является бросок игральной кости. В этом случае есть шесть равновероятных событий: выпадение чисел от 1 до 6. Вероятность каждого из этих событий равна 1/6.

Если нужно решить задачу, связанную с броском кости, можно использовать равновероятные события для вычисления вероятности выпадения определенного числа или суммы чисел на костях.

Таким образом, применение равновероятных событий позволяет упростить вычисления и решить различные задачи в математике и статистике. Они являются основой для дальнейшего изучения вероятностных распределений и статистических методов.