Что такое симметричная монета в математике

Симметричная монета в математике — это монета, у которой обе стороны имеют одинаковый шанс выпасть. Узнайте, как определить симметричность монеты и как она используется в вероятностных расчетах и играх.

Симметричная монета в математике является одной из основных концепций, в которой изучается симметрия. Это особый вид монеты, который имеет определенную особенность — все его стороны и значения равны между собой. Такая монета представляет собой идеально сбалансированную фигуру, которая помогает нам понять, как работает симметрия в математике. Симметричная монета является важной концепцией и используется в различных областях математики, включая геометрию, алгебру и теорию вероятности.

Одна из особенностей симметричной монеты в математике заключается в том, что она имеет ось симметрии. Это означает, что если мы разделим монету пополам вдоль оси симметрии, то каждая половина будет выглядеть идентично другой. Это свойство симметричной монеты позволяет нам делать различные выводы и применять его в различных математических задачах.

Симметричная монета также широко используется в задачах теории вероятности. Используя симметричную монету, мы можем исследовать вероятность различных исходов подбрасывания монеты, таких как выпадение «орла» или «решки». Симметричная монета позволяет нам установить равную вероятность для каждого из этих исходов и провести различные эксперименты, чтобы узнать больше о вероятности и случайности.

Использование симметричной монеты в математике позволяет нам лучше понять и изучать принципы симметрии и их применение в различных областях математического анализа. Она является неотъемлемой частью математического образования и играет важную роль в развитии логического мышления и аналитических навыков. Поэтому понимание симметричной монеты и ее концепции является важным аспектом в изучении математики.

Симметричная монета в математике: основные понятия и свойства

Основное свойство симметричной монеты заключается в том, что при подбрасывании она имеет равные вероятности выпадения герба и решки. Таким образом, вероятность выпадения герба и решки составляет по 1/2. Это свойство может быть использовано для моделирования случайных событий, например, в задачах о броске монеты или в играх.

Симметричная монета также может быть использована в комбинаторике для решения задач на подсчет количества различных исходов. Например, при подбрасывании двух симметричных монет можно получить четыре различных исхода: герб-герб, герб-решка, решка-герб и решка-решка. Это понятие может быть расширено на более сложные задачи, включающие большее количество монет или другие комбинации.

Вероятность выпадения определенной комбинации при подбрасывании симметричных монет можно рассчитать по формуле, известной как правило умножения вероятностей. Для примера, вероятность выпадения двух гербов при подбрасывании двух монет равна 1/2 * 1/2 = 1/4.

Использование симметричной монеты в математике позволяет моделировать случайные события, решать задачи на подсчет комбинаций и вычислять вероятности. Этот концепт является важным фундаментом для понимания более сложных теоретических понятий и применений в математике и статистике.

Видео по теме:

Определение симметричной монеты

Основное свойство симметричной монеты заключается в том, что вероятности выпадения орла и решки равны между собой и составляют 0.5 (или 50%). Это связано с тем, что симметричная монета имеет одинаковую вероятность выпасть одной из сторон. Таким образом, при многократном подбрасывании симметричной монеты, количество выпадений орла и решки должно быть примерно одинаковым.

Симметричные монеты широко используются в математике для изучения вероятности. Они являются простым и понятным примером вероятностного эксперимента, который помогает изучать основные принципы и законы вероятности.

Симметричная монета также может использоваться для моделирования случайных процессов, например, для принятия решений в условиях неопределенности. Она помогает представить случайность и вероятность в математической форме и анализировать различные сценарии.

Принцип работы симметричной монеты

Принцип работы симметричной монеты заключается в том, что при подбрасывании монеты у нас есть равные шансы получить орла или решку. Это происходит из-за симметричной формы монеты, которая обеспечивает равновероятность выпадения каждой стороны.

Для проведения эксперимента с симметричной монетой, необходимо подбросить ее и наблюдать, какая сторона (орел или решка) окажется верхней. Вероятность выпадения орла и решки при этом равна 0,5 или 50%, так как у нас есть всего две возможности и они равновероятны.

Симметричная монета является простым примером для изучения вероятностей и может быть использована для моделирования различных ситуаций. Например, при подбрасывании монеты можно определить вероятность выпадения определенной стороны и использовать это для принятия решений или прогнозирования исходов случайных событий.

Важно отметить, что симметричная монета является идеализированной моделью, и в реальности могут существовать монеты, которые не являются абсолютно симметричными. В таких случаях вероятность выпадения орла или решки может отличаться от 50% и зависеть от особенностей монеты.

Примеры применения симметричной монеты

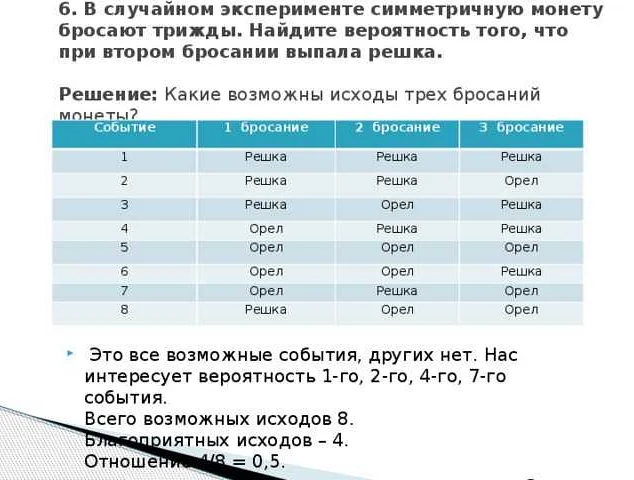
Одним из примеров применения симметричной монеты является моделирование подбрасывания монеты. При подбрасывании симметричной монеты существует два возможных исхода: орел или решка. Оба исхода имеют равную вероятность выпадения, поэтому симметричная монета идеально подходит для моделирования этой ситуации.

Еще одним примером применения симметричной монеты является моделирование справедливой игры на удачу. Представим, что у нас есть игра, в которой игрок может выиграть или проиграть с равной вероятностью. В этом случае симметричная монета может быть использована для определения исхода игры: орел означает выигрыш, а решка – проигрыш.

Также симметричная монета может быть использована для моделирования случайных событий в экономике. Например, при моделировании изменения цены акций на рынке, можно использовать симметричную монету для определения двух возможных направлений движения цены: повышение или понижение.

В образовании симметричная монета может быть использована для простого понятия вероятности. Ученикам можно предложить провести серию экспериментов с подбрасыванием монеты и записать результаты. Затем они могут вычислить отношение числа орлов к общему числу бросков и сравнить его с ожидаемой вероятностью 1/2. Это поможет учащимся понять, как вероятность может быть описана и измерена.

Все эти примеры демонстрируют важность и полезность симметричной монеты в различных областях, связанных с вероятностью и моделированием случайности.

Расчеты с использованием симметричной монеты

Использование симметричной монеты позволяет проводить различные расчеты и эксперименты в математике. Например, можно рассчитать вероятность выпадения определенного количества орлов или решек при нескольких подряд идущих бросках монеты.

Для расчетов с использованием симметричной монеты можно применять различные методы. Один из них — это использование комбинаторики. Например, чтобы рассчитать вероятность выпадения двух орлов и одной решки при трех бросках монеты, можно использовать формулу сочетаний. В данном случае, количество сочетаний будет равно 3, так как есть три возможных исхода: орел, решка или орел. Таким образом, вероятность выпадения данной комбинации будет равна 1/3.

Кроме того, с использованием симметричной монеты можно проводить эксперименты для проверки различных гипотез и теорий в математике и статистике. Например, можно проверить гипотезу о том, что вероятность выпадения орла равна вероятности выпадения решки. Для этого необходимо провести большое количество бросков монеты и подсчитать количество выпадений орла и решки. Если разница между этими значениями будет незначительной, то гипотеза будет подтверждена.

Таким образом, расчеты с использованием симметричной монеты позволяют проводить различные эксперименты и расчеты в математике и статистике. Они помогают выявить закономерности и установить вероятности различных исходов при бросании монеты.

Особенности симметричной монеты в математическом моделировании

Одной из особенностей симметричной монеты является равновероятность выпадения орла или решки при каждом подбрасывании. Это означает, что вероятность выпадения орла и решки равны 0.5 или 50%. Такая монета часто используется в математических моделях, чтобы исследовать вероятностные явления и проводить различные эксперименты.

Симметричная монета также является основой для изучения более сложных случайных величин и вероятностных распределений. Например, с помощью монеты можно моделировать бросок двух или более монет, где каждая монета может выпасть орлом или решкой независимо от других.

Симметричная монета часто используется в играх и ставках, где случайность сыгранного исхода является ключевым фактором. Она также используется в обучении статистике и теории вероятностей для примеров и задач, поскольку позволяет легко демонстрировать основные понятия и формулы.

Важно понимать, что симметричная монета является идеализацией реального мира и успешно применяется в математическом моделировании для упрощения и изучения случайных явлений.

Преимущества и недостатки использования симметричной монеты

Преимущества использования симметричной монеты:

• Простота использования: симметричная монета позволяет проводить эксперименты и решать задачи без необходимости учитывать вероятности выпадения той или иной стороны. Это упрощает математические вычисления и позволяет сосредоточиться на сути задачи.
• Удобство моделирования: симметричная монета может использоваться для моделирования различных случайных событий, таких как подбрасывание монеты или принятие решения методом подбрасывания. Это помогает понять и изучить основы вероятности и случайных процессов.
• Объективность результатов: использование симметричной монеты в экспериментах позволяет получать объективные результаты, так как обе стороны монеты равноправны и вероятность выпадения каждой стороны одинакова.

Недостатки использования симметричной монеты:

• Ограниченность модели: симметричная монета не может быть использована для моделирования событий, где вероятности выпадения разных сторон монеты различны. Например, если задача требует учёта вероятности выпадения орла и решки с разными весами, симметричная монета не подходит.
• Ограничение на количество сторон: симметричная монета имеет только две стороны, что может быть недостаточно для моделирования некоторых сложных случайных событий. Например, если требуется моделировать выбор из трех вариантов, симметричная монета не подходит.
• Неучет специфики задачи: в некоторых задачах и экспериментах требуется учитывать специфику событий и вероятности их выпадения. В таких случаях использование симметричной монеты может быть недостаточно точным и представлять ограничения.

В целом, использование симметричной монеты в математике имеет свои преимущества и недостатки, которые следует учитывать при выборе метода моделирования случайных событий и решении задач. В зависимости от поставленной задачи, может быть более подходящим выбрать другой инструмент для моделирования или решения вероятностных задач.

Исторический контекст и развитие симметричной монеты

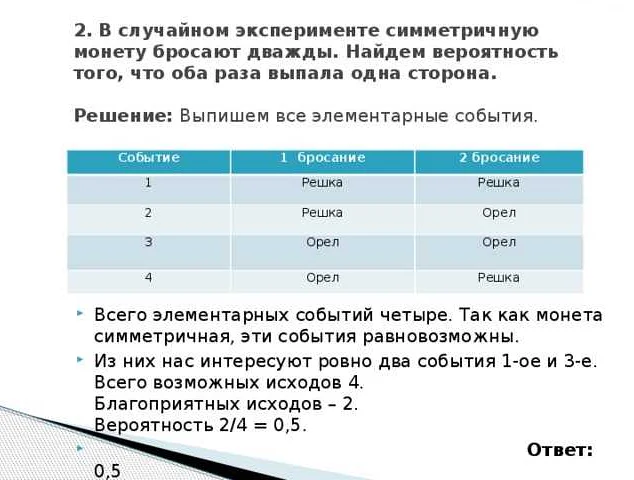
В античное время симметричная монета имела вид сбалансированного круга с изображением богини Афины на одной стороне и символами города-государства на другой стороне. Это был символ гармонии и равновесия.

В средние века симметричные монеты стали широко использоваться во многих странах мира. Они были сделаны из драгоценных металлов, таких как золото и серебро, и имели различные гербы и королевские символы на обеих сторонах монеты.

С развитием торговли и экономики в современном мире, симметричные монеты стали все более стандартизованными. Они получили определенные номиналы и стандартные размеры. Каждая страна имеет свою собственную систему симметричных монет, и они широко используются для обмена и проведения различных финансовых операций.

Симметричные монеты играют важную роль в обществе, они не только являются средством обмена, но и отражают культурные и исторические особенности каждой страны. Они являются важным источником информации для исследования истории и культуры.

Вопрос-ответ:

Что такое симметричная монета в математике?

Симметричная монета в математике — это монета, которая имеет одинаковые вероятности выпадения герба и решки при подбрасывании. То есть, если монету подбросить достаточное количество раз, вероятность выпадения герба будет примерно равна вероятности выпадения решки.

Каким образом определяется вероятность выпадения герба или решки на симметричной монете?

Вероятность выпадения герба или решки на симметричной монете определяется путем подсчета всех возможных исходов и разделения их на количество возможных исходов. Например, если монету подбросили 100 раз, то вероятность выпадения герба будет равна количеству исходов, когда выпал герб, деленному на общее количество исходов (100).

Может ли симметричная монета давать неравные вероятности выпадения герба и решки в реальности?

В идеальных условиях симметричная монета должна давать равные вероятности выпадения герба и решки. Однако, в реальности могут существовать незначительные несовершенства в форме и весе монеты, а также в силе и угле подбрасывания, которые могут привести к незначительному смещению вероятности в сторону одной из сторон монеты.

Для чего используются симметричные монеты в математике?

Симметричные монеты в математике часто используются для изучения и практического применения теории вероятностей. Они являются одним из простейших математических моделей с равновероятными исходами и позволяют изучать различные случайные события и их вероятности.

Можно ли использовать симметричную монету для моделирования других случайных событий?

Да, симметричная монета может быть использована для моделирования других случайных событий, если эти события имеют два равновероятных исхода. Например, подбрасывание монеты может моделировать бросок жребия, где выпадение герба означает один исход, а выпадение решки — другой. Однако, для моделирования более сложных случайных событий, может потребоваться использование других моделей и инструментов.

Что такое симметричная монета в математике?

Симметричная монета в математике — это монета, у которой две стороны абсолютно одинаковы. Такая монета обычно используется для моделирования вероятностных экспериментов, таких как подбрасывание монеты.

Какие свойства имеет симметричная монета в математике?

Симметричная монета в математике обладает несколькими свойствами. Во-первых, вероятность выпадения орла и решки при подбрасывании такой монеты равна 0,5 или 50%. Во-вторых, каждое подбрасывание монеты является независимым событием, то есть результат одного подбрасывания не влияет на результат следующего подбрасывания.