Разрядные слагаемые что это в математике 3

Разрядные слагаемые в математике 3 – это числа, которые составляют сумму или разность. Они помогают разбить сложную задачу на более простые и облегчают ее решение. Узнайте, как использовать разрядные слагаемые для упрощения математических операций и решения уравнений.

Разрядные слагаемые – это числа, в которых каждая цифра занимает определенное место, или разряд, в числе. Понимание и использование разрядных слагаемых является важной математической навыком, который помогает нам разбираться в больших числах и выполнять сложение и вычитание с легкостью.

Когда мы складываем или вычитаем числа, мы начинаем с младших разрядов и движемся к старшим разрядам. Например, в числе 453, 4 является цифрой в сотнях, 5 — в десятках и 3 — в единицах. Когда мы складываем два числа, мы складываем цифры в каждом разряде по отдельности. Если сумма превышает 9, то мы оставляем единицы и переносим десятки на следующий разряд.

Пример: при сложении 453 и 297 мы сначала складываем цифры в единицах (3 + 7 = 10), получаем 0 в единицах и переносим 1 в десятки. Затем складываем цифры в десятках (5 + 9 = 14), получаем 4 в десятках и переносим 1 в сотни. Наконец, складываем цифры в сотнях (4 + 2 = 6), получаем 6 в сотнях. Итоговая сумма равна 746.

Разрядные слагаемые помогают нам легко и точно выполнять сложение и вычитание. Они также пригодятся при работе с большими числами, например, при умножении и делении. Понимание разрядов и их значений поможет нам легче разбираться в числах и решать сложные математические задачи.

Определение и примеры

Для объяснения этого концепта, рассмотрим число 12345.

РазрядЦифраСлагаемое

10^4	1	10000
10^3	2	2000
10^2	3	300
10^1	4	40
10^0	5	5

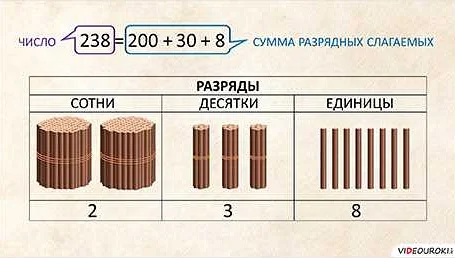
Таким образом, число 12345 можно записать как сумму разрядных слагаемых: 10000 + 2000 + 300 + 40 + 5.

Использование разрядных слагаемых позволяет анализировать и работать с числами в более удобной форме, особенно при выполнении операций, таких как сложение и вычитание.

Значение в различных математических операциях

Разрядные слагаемые могут быть использованы в различных математических операциях для упрощения вычислений и более удобного представления чисел.

В сложении разрядные слагаемые позволяют разбить числа на отдельные разряды, что упрощает процесс сложения. Например, при сложении чисел 456 и 789, мы можем разложить их на разряды: 400 + 50 + 6 и 700 + 80 + 9. Затем мы можем сложить каждый разряд отдельно: 400 + 700 = 1100, 50 + 80 = 130, 6 + 9 = 15. И наконец, мы можем сложить полученные результаты: 1100 + 130 + 15 = 1245.

В вычитании разрядные слагаемые позволяют провести вычитание по разрядам, что также упрощает вычисления. Например, при вычитании чисел 789 из 456, мы можем разложить их на разряды: 400 — 700, 50 — 80 и 6 — 9. Затем мы можем провести вычитание в каждом разряде отдельно: 400 — 700 = -300, 50 — 80 = -30, 6 — 9 = -3. И, наконец, мы можем сложить полученные результаты: -300 — 30 — 3 = -333.

В умножении разрядные слагаемые позволяют выполнять умножение по разрядам и суммировать полученные произведения. Например, при умножении чисел 456 и 789, мы можем разложить их на разряды: 400 × 700, 400 × 80, 400 × 9, 50 × 700, 50 × 80, 50 × 9, 6 × 700, 6 × 80 и 6 × 9. Затем мы можем умножить каждый разряд отдельно и сложить полученные произведения: 400 × 700 = 280000, 400 × 80 = 32000, 400 × 9 = 3600, 50 × 700 = 35000, 50 × 80 = 4000, 50 × 9 = 450, 6 × 700 = 4200, 6 × 80 = 480 и 6 × 9 = 54. И, наконец, мы можем сложить все полученные произведения: 280000 + 32000 + 3600 + 35000 + 4000 + 450 + 4200 + 480 + 54 = 360784.

Таким образом, разрядные слагаемые помогают упростить вычисления в различных математических операциях и делают их более наглядными и понятными.

Применение в расчетах

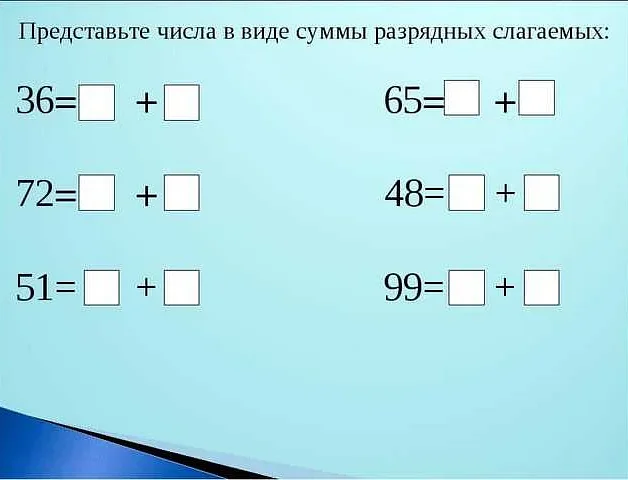
Разрядные слагаемые широко используются при выполнении сложения и вычитания чисел. При сложении двух многозначных чисел, каждое разрядное слагаемое представляет собой сумму цифр в соответствующем разряде. Например, при сложении чисел 345 и 678, разрядные слагаемые будут: 3+6=9 в разряде сотен, 4+7=11 (единица переносится в разряд тысяч) в разряде десятков, и 5+8=13 (единица переносится в разряд сотен) в разряде единиц.

При вычитании чисел, разрядные слагаемые представляют разность цифр в соответствующем разряде. Например, при вычитании числа 678 из 943, разрядные слагаемые будут: 9-6=3 в разряде сотен, 4-7=-3 (единица переносится из разряда сотен) в разряде десятков, и 3-8=-5 (единица переносится из разряда десятков) в разряде единиц.

Разрядные слагаемые также могут быть использованы при выполнении умножения чисел. При умножении двух многозначных чисел, каждое разрядное слагаемое представляет собой произведение цифр в соответствующем разряде. Например, при умножении чисел 345 и 678, разрядные слагаемые будут: 5*8=40 в разряде единиц, 4*7+5*6=58 (единица переносится в разряд десятков) в разряде десятков, и 3*6+4*8=38 (единица переносится в разряд сотен) в разряде сотен.

Таким образом, использование разрядных слагаемых позволяет разбить сложные математические операции на более простые шаги и делает расчеты более удобными и понятными.

Практические примеры использования

Разрядные слагаемые широко используются в математике и связанных областях знаний. Вот некоторые практические примеры использования:

1. Разложение числа на разрядные слагаемые: Разрядные слагаемые позволяют разложить число на сумму чисел, каждое из которых представлено одним разрядом. Например, число 3456 можно разложить на разрядные слагаемые 3000, 400, 50 и 6.

2. Упрощение выражений: При упрощении алгебраических выражений разрядные слагаемые могут помочь сократить сложные термины и провести арифметические операции более эффективно. Например, выражение 3x + 5x — 2x + 7x можно упростить, сгруппировав одинаковые слагаемые: (3 + 5 — 2 + 7)x = 13x.

3. Решение уравнений: Разрядные слагаемые также могут быть полезны при решении уравнений. Они могут помочь выделить одинаковые слагаемые и сократить уравнение до более простой формы. Например, при решении уравнения 2x + 3x — 5x = 10, мы можем сгруппировать одинаковые слагаемые: (2 + 3 — 5)x = 10, что приводит к уравнению 0x = 10.

4. Работа с большими числами: Разрядные слагаемые особенно полезны при работе с большими числами, которые трудно представить в обычном виде. Они позволяют разбить число на более мелкие части и облегчить выполнение арифметических операций. Например, при сложении чисел 123456789 и 987654321 мы можем сначала сложить разрядные слагаемые: 100000000 + 20000000 + 3000000 + 400000 + 50000 + 6000 + 700 + 80 + 9 = 1111111110.

Практическое использование разрядных слагаемых помогает решать различные задачи, проводить упрощения выражений и работать с большими числами более эффективно.

Преимущества использования разрядных слагаемых

Использование разрядных слагаемых в математике имеет несколько преимуществ:

1.	Упрощение сложных вычислений.
2.	Повышение точности результатов.
3.	Облегчение понимания числовых операций.

Разрядные слагаемые позволяют разбивать сложные числа на более простые компоненты, что упрощает выполнение арифметических операций с ними. Например, при сложении или вычитании чисел с большим количеством разрядов, использование разрядных слагаемых позволяет сосредоточиться на каждом разряде по отдельности, что существенно упрощает процесс вычислений.

Кроме того, использование разрядных слагаемых повышает точность результатов математических операций. В процессе вычислений каждый разряд обрабатывается отдельно, что позволяет избегать округления и потери точности при работе с большими числами.

Наконец, использование разрядных слагаемых способствует более глубокому пониманию числовых операций. Разбиение чисел на отдельные разряды позволяет лучше увидеть и понять их структуру и взаимосвязи. Это особенно полезно при обучении и изучении математики, так как помогает студентам лучше осознавать процессы, происходящие при выполнении различных операций.

Сравнение с другими методами

В отличие от других методов, таких как столбиковое сложение или вычитание, метод разрядных слагаемых позволяет решать сложные задачи с большими числами более быстро и эффективно.

Кроме того, метод разрядных слагаемых обладает свойством независимости разрядов, что позволяет выполнять операции с каждым разрядом отдельно. Это значит, что можно сравнивать числа разных разрядов, что упрощает процесс вычитания и сложения.

Таким образом, метод разрядных слагаемых является предпочтительным методом для решения сложных задач с числами и позволяет выполнять операции более быстро и удобно.

Вопрос-ответ:

Какие разрядные слагаемые существуют в математике?

В математике существуют разрядные слагаемые единиц, десятков, сотен, тысяч и так далее. Каждое разрядное слагаемое представляет собой цифру в числе, которая умножается на соответствующую степень десятки.

Как использовать разрядные слагаемые в сложении чисел?

При сложении двух чисел с использованием разрядных слагаемых, вы выравниваете числа по разрядам и складываете соответствующие разрядные слагаемые. Например, при сложении чисел 123 и 456, вы сначала сложите единицы, затем десятки и так далее.

Как использовать разрядные слагаемые в вычитании чисел?

При вычитании чисел с использованием разрядных слагаемых, вы также выравниваете числа по разрядам и вычитаете соответствующие разрядные слагаемые. Если разрядное слагаемое числа, из которого вы вычитаете, меньше разрядного слагаемого числа, которое вы вычитаете, то вы занимаете единицу из следующего разряда и продолжаете вычитание.

Какие преимущества есть в использовании разрядных слагаемых в математике?

Использование разрядных слагаемых в математике упрощает сложение и вычитание чисел, особенно когда числа имеют много разрядов. Оно помогает визуализировать и понять, как происходят операции сложения и вычитания, а также улучшает понимание позиционной системы счисления.

Как можно использовать разрядные слагаемые для упрощения умножения и деления?

Разрядные слагаемые могут быть использованы для упрощения умножения и деления чисел путем разложения чисел на разрядные слагаемые и умножения или деления разрядных слагаемых по отдельности. Это может упростить процесс умножения и деления и уменьшить вероятность ошибок.

Что такое разрядные слагаемые?

Разрядные слагаемые — это числа, которые входят в состав числа и представляют его разряды. Например, в числе 543 разрядные слагаемые это 500, 40 и 3.

Источники и дополнительная информация

Если вы заинтересовались темой разрядных слагаемых и хотите узнать больше о их использовании в математике, рекомендуем обратиться к следующим источникам:

1. Учебники по математике:

— Школьный курс математики: под редакцией Н. Я. Виленкина, М. И. Бутузова, Н. Б. Истомина;

— Математика: учебник для 7 класса. Авторы: Н. Б. Истомина, М. И. Бутузов, Л. Н. Горбов.

2. Интернет-ресурсы:

— Статья «Разрядные слагаемые» на сайте «Математика для всех» (www.mathdoza.ru);

— Видеоурок «Разрядные слагаемые» на YouTube-канале «Математика с Мариной» (www.youtube.com/matematikasmarinoy).

Изучение разрядных слагаемых позволит вам лучше понять числовую систему и упростить вычисления, особенно при работе с большими числами. Удачи в изучении!

Видео по теме: