Что изучает информатика математические методы решения задач

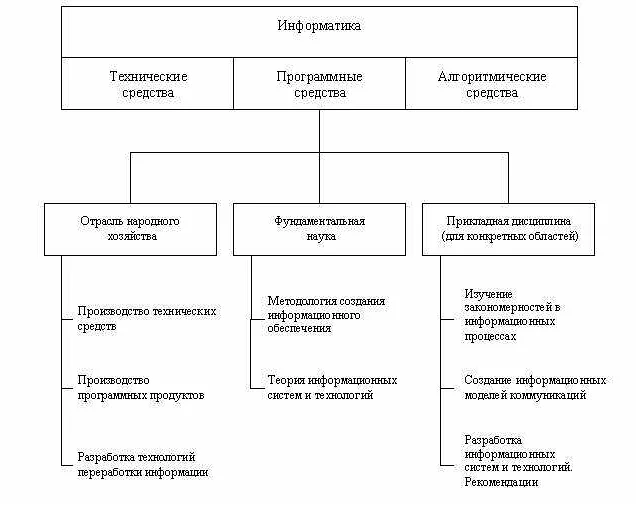
Статья рассказывает о том, как информатика применяет математические методы для решения различных задач. Она объясняет, какие математические концепции и инструменты используются в информатике и как они помогают в анализе данных, разработке алгоритмов и создании компьютерных моделей. Важность математического подхода в информатике подчеркивается, и приводятся примеры, как математические методы помогают в решении конкретных задач, таких как оптимизация, моделирование и шифрование информации.

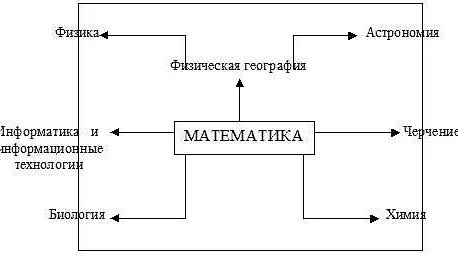
Информатика — это наука, которая изучает методы обработки информации с использованием компьютеров. Она тесно связана с математикой, так как математические методы являются основой для решения сложных задач в информатике. Математика предоставляет инструменты и подходы, которые позволяют анализировать и описывать различные аспекты информационного мира, а также разрабатывать эффективные алгоритмы и структуры данных для их обработки.

Одна из ключевых областей, где математические методы играют важную роль, — это алгоритмы. Алгоритм — это последовательность шагов, которая описывает решение задачи. Для разработки эффективных алгоритмов необходимо применять математические методы, такие как теория графов, комбинаторика, теория вероятностей и логика. Эти методы позволяют анализировать сложность алгоритмов, оптимизировать их работу и оценивать вероятность получения правильного результата.

Математические методы также играют важную роль в разработке и анализе структур данных. Структуры данных — это специальные формы организации и хранения информации, которые позволяют эффективно обрабатывать данные. Для проектирования и оценки структур данных необходимо использовать математические методы, такие как теория графов, теория множеств, математическая логика и алгебра. Эти методы позволяют анализировать свойства структур данных, оптимизировать их работу и доказывать их корректность и эффективность.

Таким образом, математические методы играют важную роль в информатике, предоставляя инструменты и подходы для решения сложных задач. Они позволяют разрабатывать эффективные алгоритмы и структуры данных, а также анализировать их свойства и оценивать их работу. Понимание и применение математических методов является необходимым навыком для успешной работы в области информатики.

Важность математических методов в информатике

Математические методы играют ключевую роль в развитии и применении информатики. Они обеспечивают фундаментальную базу для решения сложных задач в области компьютерных наук.

Одним из основных преимуществ математических методов является их точность и строгость. Они позволяют разработчикам программного обеспечения создавать надежные и эффективные алгоритмы, которые работают с высокой степенью достоверности.

Математические методы также обеспечивают абстрактное мышление и способность анализировать сложные проблемы. Они позволяют программистам разбивать сложные задачи на более простые подзадачи и решать их последовательно.

Кроме того, математические методы позволяют оптимизировать процессы и улучшать производительность компьютерных систем. Они используются для определения сложности алгоритмов, оценки времени выполнения программ и прогнозирования эффективности решений.

Важно отметить, что математические методы необходимы не только для разработки программного обеспечения, но и для решения широкого спектра задач в информатике, таких как анализ данных, машинное обучение, криптография и другие.

Таким образом, математические методы являются неотъемлемой частью информатики и играют важную роль в ее развитии. Они обеспечивают основу для решения сложных задач, оптимизации процессов и создания надежных и эффективных программных решений.

Видео по теме:

Математика как основа информатики

Основные области математики, которые широко применяются в информатике, включают:

Область математикиРоль в информатике

Теория графов	Используется для моделирования и анализа сетей, алгоритмов поиска и оптимизации
Теория вероятностей	Применяется для оценки и анализа случайных процессов, статистического моделирования
Дискретная математика	Обеспечивает основы для работы с дискретными структурами, такими как биты, байты и другие
Линейная алгебра	Используется для работы с матрицами, векторами и линейными пространствами в алгоритмах и графическом программировании

Математические методы также играют важную роль в криптографии, компьютерном зрении, машинном обучении, оптимизации и других областях информатики. Использование математических методов позволяет информатикам разрабатывать эффективные и надежные алгоритмы, а также проводить анализ и прогнозирование результатов вычислительных процессов.

Роль алгоритмов в информатике

Алгоритмы в информатике используются для решения множества задач, таких как сортировка данных, поиск наибольшего значения, построение графов и многое другое. Они применяются в различных областях, включая программирование, базы данных, искусственный интеллект, криптографию и т.д.

Одна из основных задач алгоритмов — повышение эффективности и оптимизация работы компьютерных систем. С помощью алгоритмов можно достичь более быстрой обработки данных, экономии ресурсов и повышения производительности.

В информатике существует множество различных алгоритмических подходов, каждый из которых имеет свои преимущества и ограничения. Некоторые из наиболее известных алгоритмов включают в себя сортировку пузырьком, поиск в ширину, поиск в глубину, алгоритм Дейкстры и многое другое.

Разработка и анализ алгоритмов является важной частью обучения в области информатики. Студенты изучают различные методы и подходы к разработке алгоритмов, а также изучают алгоритмическую сложность и анализ эффективности алгоритмов.

ПримерОписание

Сортировка пузырьком	Алгоритм сортировки, основанный на сравнении пар соседних элементов и их обмене в случае необходимости.
Поиск в ширину	Алгоритм поиска в графе или дереве, который ищет все вершины, доступные из начальной вершины на данной глубине, а затем переходит на следующую глубину.
Алгоритм Дейкстры	Алгоритм на графах, который находит кратчайший путь от одной вершины к остальным.

Таким образом, алгоритмы играют фундаментальную роль в информатике, обеспечивая решение различных задач и повышая эффективность работы компьютерных систем.

Значение логики в решении задач

Логика играет важную роль в решении задач в информатике. Она помогает нам анализировать проблемы и находить правильные решения.

Логические операции, такие как «и», «или» и «не», позволяют нам создавать условия для выполнения определенных действий. Например, при написании программы, логические операторы позволяют нам проверять, выполняются ли определенные условия, чтобы принять правильное решение.

Логическое мышление также позволяет нам разбивать сложные задачи на более простые подзадачи. Мы можем анализировать каждую часть задачи по отдельности, а затем объединить результаты для получения общего решения.

Кроме того, логика помогает нам избегать ошибок и неоднозначностей в решении задач. Она позволяет нам проверять наличие противоречий и устанавливать правильные связи между различными элементами задачи.

Все это делает логику неотъемлемой частью процесса решения задач в информатике. Без умения мыслить логически и применять логические операции, трудно достичь успешных результатов в программировании и других областях информатики.

Применение теории графов в информатике

Применение теории графов в информатике широко распространено и находит применение во многих областях. Она позволяет моделировать и анализировать различные системы и процессы, используя графовые структуры.

Одним из основных применений теории графов в информатике является анализ и поиск путей в графах. Это может быть поиск кратчайшего пути между двумя вершинами, определение наиболее эффективного пути или анализ структуры и свойств графа.

Теория графов также находит применение в алгоритмах и структурах данных. Графы могут быть использованы для представления различных объектов и связей между ними, что позволяет эффективно решать множество задач, таких как поиск путей, обходы графов и многое другое.

Еще одним важным применением теории графов является анализ социальных сетей. Графы позволяют моделировать связи между людьми, интересы и предпочтения, исследовать взаимодействия внутри сети и предсказывать поведение пользователей.

Теория графов также широко применяется в сетях и телекоммуникациях. Графы могут быть использованы для моделирования и анализа сетевой топологии, оптимизации маршрутов и планирования сетевых ресурсов.

В заключение, применение теории графов в информатике имеет широкий спектр применений. Она позволяет анализировать сложные системы, решать разнообразные задачи и помогает в разработке эффективных алгоритмов и структур данных.

Использование вероятности и статистики в информатике

В информатике вероятность и статистика широко используются для анализа данных, прогнозирования и оптимизации алгоритмов. Математические методы вероятности позволяют моделировать случайные события и оценивать их вероятности.

Одной из важных областей применения вероятности и статистики в информатике является машинное обучение. Вероятностные модели используются для классификации данных, анализа текстов, распознавания образов и многих других задач. Статистические методы позволяют определить наиболее значимые признаки и отфильтровать шум в данных.

Другим примером использования вероятности и статистики в информатике является анализ данных в больших объемах. Статистические методы позволяют определить закономерности и тренды в данных, провести анализ рисков и принять обоснованные решения. Такой анализ может быть использован, например, для прогнозирования поведения пользователей, оптимизации рекламных кампаний или улучшения производственных процессов.

Вероятность и статистика также находят применение при решении задач оптимизации. Оптимизационные алгоритмы могут использовать статистические методы для выбора наилучших решений из множества возможных вариантов. Вероятностные методы позволяют оценить вероятность достижения оптимального решения или найти приближенное решение в случае сложных задач.

Таким образом, использование вероятности и статистики в информатике является неотъемлемой частью разработки алгоритмов, анализа данных и принятия обоснованных решений. Знание математических методов вероятности и статистики позволяет информатикам эффективно решать задачи в различных областях, включая машинное обучение, анализ данных и оптимизацию.

Роль анализа сложности алгоритмов в информатике

Анализ сложности алгоритмов включает в себя оценку временной и пространственной сложности. Временная сложность определяет количество операций, которые должен выполнить алгоритм для решения задачи, в зависимости от размера входных данных. Пространственная сложность определяет объем памяти, необходимый для выполнения алгоритма.

Анализ сложности алгоритмов позволяет выбирать наиболее эффективные алгоритмы для решения задачи. Он помогает оптимизировать работу программы, уменьшить нагрузку на ресурсы компьютера и сократить время выполнения алгоритма. Благодаря анализу сложности алгоритмов можно сравнивать различные подходы к решению задачи и выбирать наиболее оптимальный.

Анализ сложности алгоритмов также является основой для решения многих теоретических и практических проблем в информатике. Он позволяет проверять корректность алгоритмов, доказывать их свойства и устанавливать границы их эффективности. Без анализа сложности алгоритмов невозможно разработать эффективные программы и системы, способные работать с большими объемами данных.

Таким образом, анализ сложности алгоритмов играет ключевую роль в информатике, позволяя оптимизировать работу программ и разрабатывать эффективные решения для широкого спектра задач.

Применение теории чисел в информатике

В информатике теория чисел используется для решения таких задач, как:

1.	Проверка числа на простоту
2.	Генерация простых чисел
3.	Факторизация чисел
4.	Решение сравнений и китайской теоремы об остатках
5.	Шифрование и дешифрование информации

Проверка числа на простоту является одной из основных операций в информатике, так как простые числа используются в криптографии и алгоритмах шифрования. Теория чисел позволяет проверить, является ли число простым, используя различные алгоритмы, такие как решето Эратосфена или тест Миллера-Рабина.

Генерация простых чисел также является важной задачей, например, при генерации ключей для криптографических систем. С помощью теории чисел можно создать алгоритмы, которые генерируют большие простые числа с заданными свойствами.

Факторизация чисел играет важную роль в криптографии и криптоанализе. Теория чисел позволяет разложить число на простые множители и определить его простые делители, что может быть использовано для взлома различных шифров.

Решение сравнений и китайской теоремы об остатках также находит применение в информатике, например, при решении задач линейной алгебры или при работе с модулярной арифметикой.

Наконец, теория чисел используется для разработки алгоритмов шифрования и дешифрования информации. Некоторые известные криптографические системы, такие как RSA или шифр Эль-Гамаля, основаны на теории чисел и используют математические операции с большими числами.

Таким образом, теория чисел является важной и неотъемлемой частью информатики, которая позволяет решать различные задачи, связанные с числами и их свойствами.

Значение математической линейной алгебры в информатике

Одним из основных объектов изучения линейной алгебры являются линейные преобразования. В информатике линейные преобразования широко применяются для обработки и анализа данных, таких как изображения, звуковые сигналы и тексты. Например, с помощью матриц можно осуществлять преобразования изображений, фильтрацию звука, компрессию данных и многое другое.

Линейная алгебра также играет важную роль в проектировании и анализе алгоритмов. Многие алгоритмы, используемые в информатике, основаны на математических концепциях линейной алгебры, таких как матрицы, векторы и системы линейных уравнений. Например, алгоритмы машинного обучения, алгоритмы сжатия данных и алгоритмы оптимизации часто используют матрицы и векторы для представления и обработки информации.

Кроме того, линейная алгебра является важным инструментом для моделирования и оптимизации различных систем и процессов. С ее помощью можно описывать и анализировать сложные системы, такие как сети передачи данных, экономические модели и физические процессы. Математические методы линейной алгебры позволяют строить модели, решать их и проводить численные эксперименты для получения реальных результатов.

В целом, математическая линейная алгебра играет важную роль в информатике. Ее методы и концепции используются для разработки эффективных алгоритмов, обработки и анализа данных, моделирования и оптимизации систем. Понимание и применение математической линейной алгебры позволяет информатикам эффективно работать с разнообразной информацией и решать сложные задачи в своей профессиональной деятельности.

Вопрос-ответ:

Зачем информатикам использовать математические методы для решения задач?

Использование математических методов позволяет информатикам более точно и эффективно решать сложные задачи, а также обеспечивает математическую обоснованность полученных результатов. Математика является основой информатики и позволяет разрабатывать и анализировать алгоритмы, проводить вычисления, оптимизировать процессы и доказывать корректность программного обеспечения.

Какие математические методы используются в информатике?

В информатике используются различные математические методы, включая теорию графов, логику, теорию вероятностей, дискретную математику, алгебру и др. Теория графов позволяет моделировать и анализировать связи между объектами в системах. Логика предоставляет инструменты для формализации и доказательства утверждений. Теория вероятностей используется для моделирования случайных процессов и оценки вероятностей событий. Дискретная математика и алгебра используются для разработки алгоритмов и обработки данных.

Как математические методы помогают в разработке алгоритмов?

Математические методы позволяют анализировать задачи и разрабатывать оптимальные алгоритмы для их решения. Например, в теории графов используются алгоритмы обхода и поиска кратчайших путей, которые помогают найти оптимальные пути в сетях. Теория вероятностей и статистика позволяют оптимизировать алгоритмы, учитывая вероятность наступления различных событий. Дискретная математика предоставляет инструменты для работы с дискретными объектами, такими как биты и целые числа, что особенно важно для информатики.

Как математические методы помогают доказывать корректность программного обеспечения?

Математические методы позволяют формально доказывать корректность программного обеспечения. Например, в теории формальных языков используется формальное определение синтаксиса и семантики языков программирования, что позволяет доказывать правильность программы на основе формальных правил. Логика и алгебра используются для формализации и доказательства утверждений о поведении программы. Доказательства корректности программ помогают удостовериться, что программа работает правильно и не содержит ошибок.