Сколько частей в математике

Статья рассказывает о количестве разделов в математике и о том, как они взаимосвязаны. Узнайте, сколько частей в математике и как они помогают решать различные математические задачи.

Математика — это наука, которая изучает структуру, свойства и взаимосвязи чисел, фигур, алгебраических объектов и других математических объектов. Она является одной из самых старых наук и имеет множество разделов и направлений, каждое из которых изучает определенные аспекты математики.

Основные разделы математики включают:

Арифметика — раздел математики, который изучает числа и основные арифметические операции: сложение, вычитание, умножение и деление. Она также включает в себя изучение различных свойств чисел, таких как простые числа, рациональные и иррациональные числа, пропорции и проценты.

Алгебра — это раздел математики, который изучает алгебраические структуры, включая операции над переменными и алгебраическими выражениями. Она также включает в себя изучение линейных и квадратных уравнений, систем уравнений, матриц и векторов.

Геометрия — это раздел математики, который изучает фигуры, их свойства и взаимное расположение в пространстве. Он также включает в себя изучение геометрических преобразований, таких как повороты, сдвиги и отражения.

Кроме того, существуют и другие разделы математики, такие как математическая логика, математический анализ, теория вероятностей и математическая статистика, дискретная математика и теория чисел. Каждый из этих разделов имеет свои специфические методы и приложения в науке, технике и других областях знания.

Математика играет ключевую роль в развитии науки и технологии, и ее различные разделы и направления позволяют изучать и моделировать разнообразные явления и процессы в природе и обществе. Она также является основой для многих других наук и представляет интерес для людей, увлеченных абстрактным мышлением и решением сложных задач.

Основные разделы математики

Алгебра: это раздел математики, который изучает символическое представление и манипулирование абстрактными объектами, такими как числа, переменные и операции. В алгебре исследуется алгебраические уравнения, системы уравнений, полиномы и другие алгебраические структуры.

Анализ: это раздел математики, который изучает предельные значения, непрерывность, дифференцирование, интегрирование и другие понятия, связанные с изменением и приближением. Анализ позволяет изучать функции, исследовать их свойства и применять их в решении задач.

Геометрия: это раздел математики, который изучает формы, размеры, относительное положение и свойства геометрических объектов, таких как точки, линии, плоскости и тела. Геометрия исследует геометрические свойства и применяется в различных областях, включая физику, инженерию и компьютерную графику.

Теория вероятностей и математическая статистика: это раздел математики, который изучает случайные явления, вероятность и статистические методы. Теория вероятностей позволяет оценивать вероятности различных исходов событий, а математическая статистика позволяет анализировать данные и делать выводы на основе статистических методов.

Дискретная математика: это раздел математики, который изучает объекты и структуры, которые имеют конечное или счетное число элементов. В дискретной математике исследуются комбинаторика, теория графов, теория кодирования и другие области, которые имеют практическое применение в компьютерных науках и других областях.

Математическая логика: это раздел математики, который изучает формальные системы, символическую логику и понятия истинности и ложности. Математическая логика позволяет анализировать и доказывать математические утверждения с помощью формальных правил.

Это лишь некоторые из основных разделов математики. Каждый из этих разделов имеет свои подразделы и специализации, которые позволяют исследовать математические структуры и применять их в различных областях знания и практики.

Арифметика

Основные понятия и принципы, изучаемые в арифметике, включают в себя:

• Натуральные числа — это числа, которые используются для подсчета предметов и обозначаются символами 1, 2, 3 и так далее.
• Целые числа — это числа, включающие натуральные числа, их отрицательные значения и ноль.
• Рациональные числа — это числа, которые можно представить в виде дробей, где числитель и знаменатель являются целыми числами.
• Десятичная система счисления — это система счисления, основанная на числе 10 и использующая десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.

Арифметика предоставляет инструменты для решения различных задач, таких как расчеты, измерения и моделирование явлений в реальном мире. Она является основой для более сложных областей математики, таких как алгебра, геометрия и анализ.

Алгебра

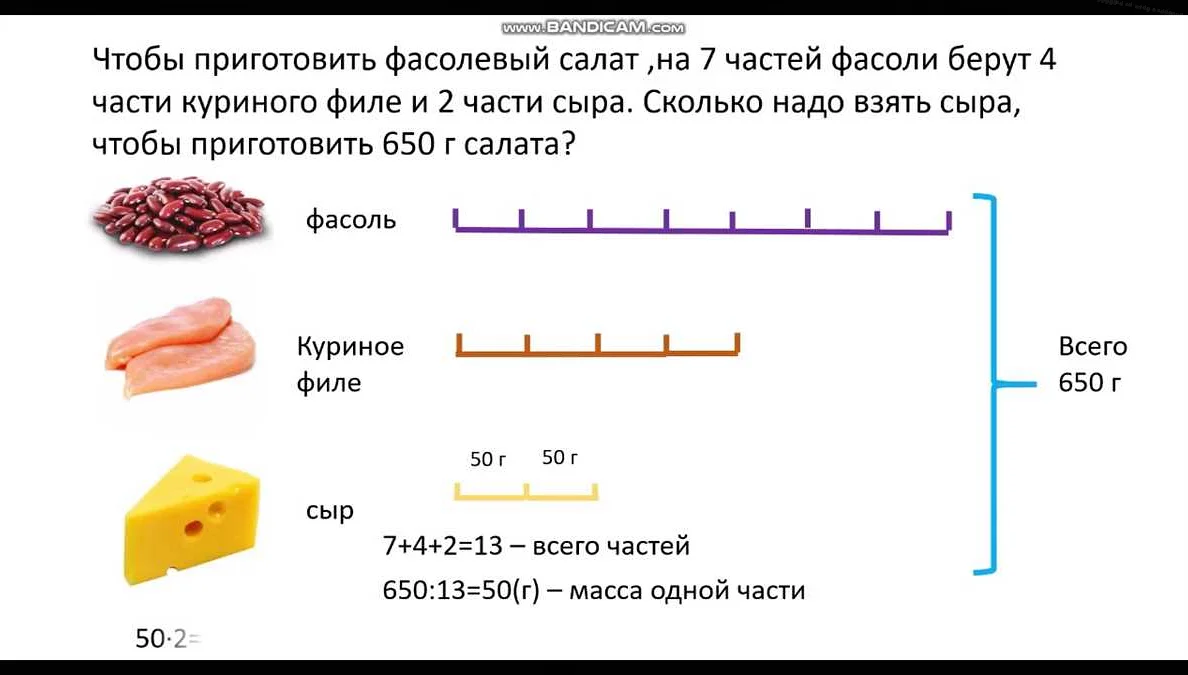
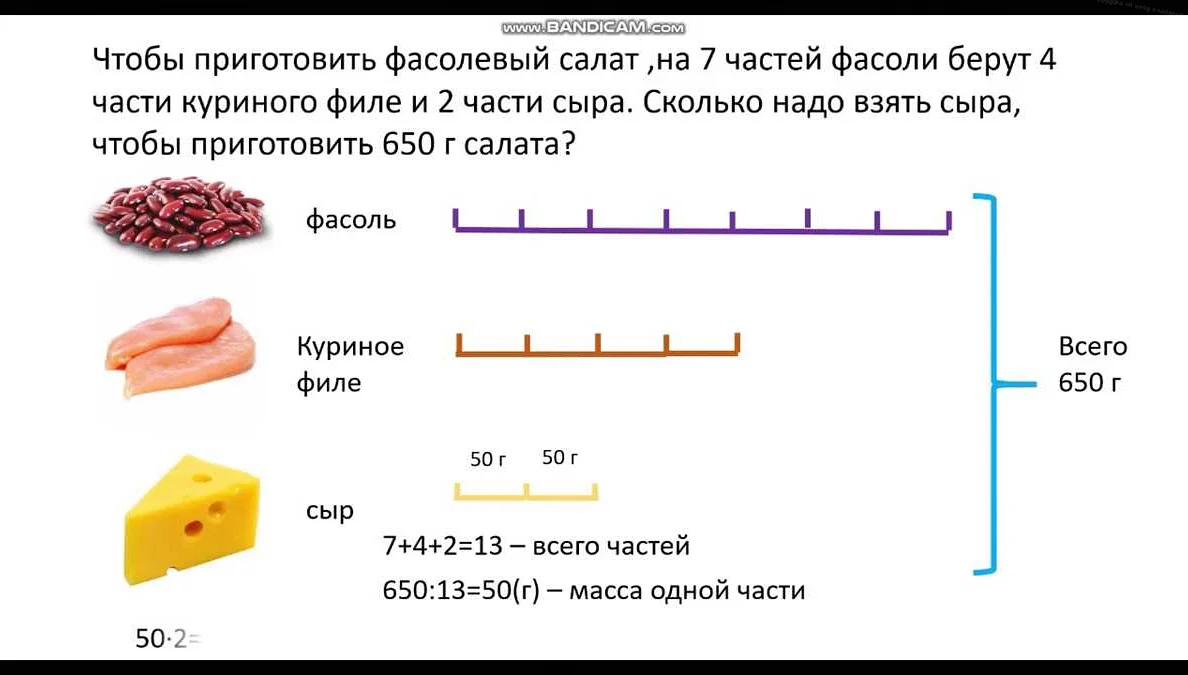
Алгебра используется для решения уравнений, систем уравнений и математических задач в различных областях, включая физику, экономику и компьютерные науки. Она также играет важную роль в анализе и теории чисел.

Основные направления в алгебре включают:

• Линейную алгебру — изучает векторные пространства, линейные операции и системы линейных уравнений.
• Абстрактную алгебру — изучает алгебраические структуры, такие как группы, кольца и поля.
• Теорию чисел — изучает свойства и взаимоотношения целых чисел и простых чисел.
• Алгебраическую геометрию — изучает алгебраические объекты, определяемые уравнениями.
• Теорию групп — изучает свойства и структуры групп.

Алгебра занимает важное место в образовании и является неотъемлемой частью программы по математике в школах и университетах.

Геометрия

Основные направления геометрии:

• Евклидова геометрия — основана на аксиомах Евклида и изучает геометрические фигуры в плоскости и пространстве.
• Аналитическая геометрия — использует методы алгебры и анализа для изучения геометрических объектов.
• Проективная геометрия — изучает свойства геометрических объектов, которые сохраняются при проективных преобразованиях.
• Дифференциальная геометрия — изучает геометрические объекты с помощью методов дифференциального исчисления.

Геометрия играет важную роль в решении различных задач, как в научных исследованиях, так и в применении в повседневной жизни. Она позволяет изучать и описывать формы и структуры объектов, а также рассчитывать их параметры и характеристики.

Математический анализ

Одним из основных понятий в математическом анализе является предел функции. Предел определяет поведение функции при стремлении аргумента к определенному значению. Производная функции показывает, как быстро меняется значение функции в каждой точке ее области определения.

Интеграл функции – это понятие, обратное производной. Он позволяет находить площади или объемы, ограниченные кривой или поверхностью.

Математический анализ имеет множество приложений в различных областях науки и техники. Он используется в физике, экономике, биологии, компьютерной графике и других дисциплинах. Понимание основных понятий и методов математического анализа является важным для практического применения математики в реальных ситуациях.

Теория вероятностей

Основные понятия теории вероятностей включают вероятность, случайную величину, событие, распределение вероятностей, математическое ожидание и другие. Вероятность — это числовая характеристика, отражающая степень возможности наступления конкретного события. Случайная величина — это величина, которая принимает различные значения в зависимости от исхода эксперимента.

Теория вероятностей также включает в себя различные методы и подходы к анализу случайных явлений. Это может быть аналитический метод, когда используются формулы и уравнения для вычисления вероятностей и статистический метод, когда проводятся эксперименты и анализируются полученные данные.

Основные понятияОписание

Вероятность	Числовая характеристика, отражающая степень возможности наступления события.
Случайная величина	Величина, которая принимает различные значения в зависимости от исхода эксперимента.
Событие	Совокупность элементарных исходов исследуемого случая.
Распределение вероятностей	Вероятностная характеристика случайной величины, задающая вероятности ее значений.
Математическое ожидание	Среднее значение случайной величины, усредненное по всем возможным исходам.

Теория вероятностей играет важную роль в принятии решений, прогнозировании событий и анализе рисков. Она позволяет оценивать вероятности различных исходов и принимать взвешенные решения на основе этих оценок.

Математическая статистика

Основная задача математической статистики – изучение случайных явлений и построение моделей, которые помогают описать и объяснить эти явления. В процессе работы с данными математическая статистика использует методы математического анализа, теории вероятностей, линейной алгебры и других математических дисциплин.

Математическая статистика разделяется на две основные области: описательную и инференциальную статистику. Описательная статистика изучает методы описания данных, включая средние значения, меры разброса, корреляцию и другие характеристики выборки.

Инференциальная статистика занимается статистическим выводом, позволяющим сделать общие заключения о генеральной совокупности на основе выборочных данных. Для этого используются методы оценки параметров и проверки гипотез.

Математическая статистика находит широкое применение в различных областях науки, промышленности и социальных науках. Она используется для анализа экономических данных, прогнозирования погоды, исследования медицинских данных, анализа социологических опросов и многих других задач.

Важным аспектом математической статистики является умение интерпретировать полученные статистические результаты и делать выводы, основанные на них. Правильное применение методов математической статистики позволяет избежать ошибок в принятии решений и дать объективную оценку рассматриваемых явлений.

Видео по теме:

Вопрос-ответ:

Какие основные разделы в математике?

Математика состоит из нескольких основных разделов, таких как арифметика, геометрия, алгебра, математический анализ, теория вероятностей и др.

Сколько всего частей в математике?

В математике существует огромное количество различных частей и подразделов. Не существует точного числа, так как новые направления исследований всегда появляются. Однако можно выделить около 20-30 основных разделов.

Какие разделы математики относятся к прикладной науке?

В прикладной науке особое значение имеют такие разделы математики, как математическая статистика, теория оптимизации, математическое моделирование, дифференциальные уравнения и т.д. Эти разделы позволяют применять математические методы для решения реальных задач в различных областях науки и техники.

Какие разделы математики относятся к теоретической науке?

К теоретической математике относятся различные абстрактные разделы математики, такие как теория множеств, математическая логика, теория чисел, теория групп и т.д. Эти разделы занимаются изучением основных понятий и структур математики без прямого применения к практическим задачам.

Какие разделы математики широко используются в компьютерных науках?

В компьютерных науках широко используются такие разделы математики, как дискретная математика, теория графов, теория алгоритмов, теория формальных языков и др. Эти разделы позволяют разрабатывать эффективные алгоритмы, анализировать сложность вычислений и решать другие задачи, связанные с обработкой информации на компьютере.

Какие основные разделы в математике?

В математике существует несколько основных разделов: алгебра, геометрия, математический анализ, теория вероятностей и математическая статистика, дискретная математика и теория чисел. Каждый из этих разделов имеет свои особенности и изучает различные аспекты математического знания.

Дискретная математика

ОбластьОписание

Теория множеств	Изучает свойства и операции над множествами, включая объединение, пересечение, разность и декартово произведение.
Теория графов	Исследует графы, которые представляют собой множество вершин, соединенных ребрами. Графы используются для моделирования отношений и связей между объектами.
Комбинаторика	Изучает комбинаторные структуры, такие как перестановки, сочетания и размещения. Ее методы применяются в задачах подсчета и упорядочивания объектов.
Теория кодирования	Разрабатывает методы кодирования и декодирования информации для передачи и хранения данных. Она имеет применения в области телекоммуникаций и информационной безопасности.
Теория вычислительных алгоритмов	Исследует различные алгоритмы и методы решения вычислительных задач. Здесь изучаются алгоритмы сортировки, поиска, графовых алгоритмов и многое другое.

Дискретная математика является основой для различных областей информатики, криптографии, теории вероятностей и других наук. Ее методы и концепции широко используются в современных технологиях и приложениях.

Математическая логика

Основные направления математической логики включают:

• Исчисление высказываний. Этот раздел занимается формализацией логических высказываний с использованием символов и правил логического вывода.
• Исчисление предикатов. В этом направлении изучается формализация и рассуждение о предикатах и кванторах, которые позволяют описывать свойства и отношения между объектами.
• Математическая модель теории множеств. В данном разделе математической логики исследуются аксиомы и правила, на которых базируется теория множеств, и строится формальная модель для этой теории.
• Модальная логика. Это направление изучает логическое рассуждение о возможности, необходимости и истинности высказываний в различных модальностях.
• Математическая индукция. В данном разделе исследуются принципы и методы математической индукции, которые используются для доказательства утверждений о целых числах и других структурах.

Математическая логика является основой для многих других разделов математики, таких как алгебра, анализ, теория вероятностей и др. Она позволяет формализовать и проверять математические рассуждения, что является важным элементом в развитии математической науки.